Содержание

Постановка задачи 2

Построение алгоритма решения 2

Алгоритм L-Shaped метода 3

Пример использования алгоритма 4

Практическая ценность L-Shaped метода 7

Практическое применение L-Shaped метода 7

Постановка задачи

Рассмотрим двухэтапную задачу квантильной оптимизации с критерием в форме математического ожидания следующего вида:

при ограничениях

,

где ,

, причём матрица Т развёрнута определённым образом (по строкам или по столбцам).

Пусть имеет конечное распределение, а именно . Тогда решение исходной задачи может быть сведено к решению задачи линейного программирования

при ограничениях

.

Однако, эта задача, если

, имеет размерность технологической матрицы , что весьма внушительно, поскольку К может быть достаточно большим числом не только потому, что велико количество возможных реализаций случайных факторов в прикладной задачи, но и потому, что может подразумеваться несколько периодов планирования.

Можно попытаться предложить некоторые варианты сведения полученной ЗЛП к ряду ЗЛП меньшей размерности.

Построение алгоритма решения

Предположим, что у нас есть некоторое субоптимальное решение , которому соответствует значение критерия второго этапа . В качестве первичной субоптимальной пары может быть взята , которая является формальным решением задачи . Смысл этого хода в том, что мы временно не используем никакой информации о втором этапе, а предполагаем, что он уже оптимизирован, насколько возможно.

Теперь, если у нас есть некоторая субоптимальная пара , то мы должны убедиться в том, что она удовлетворяет всем ограничениям задачи. Для этой проверки достаточно решить серию из К задач при ограничениях , где и - векторы невязок, I – единичная матрица, . Если для какого-либо , то как сумма невязок, и, используя двойственные переменные, получим . Всегда , так что для выполнения условий допустимости субоптимальной пары ( ) нужно потребовать , то есть

Условия оптимальности можно получить, рассматривая функцию , являющуюся выпуклой по . Тогда , где – субградиент функции в точке . С использованием двойственных переменных можно записать , , тогда , а , тем самым и для должно быть выполнено условие оптимальности .

Из этих соображений и строится алгоритм L-shaped метода.

Алгоритм l-Shaped метода

Шаг 0 (инициализация). Полагаем .

Шаг 1 (Построение субоптимального решения). Решаем ЗЛП

при ограничениях

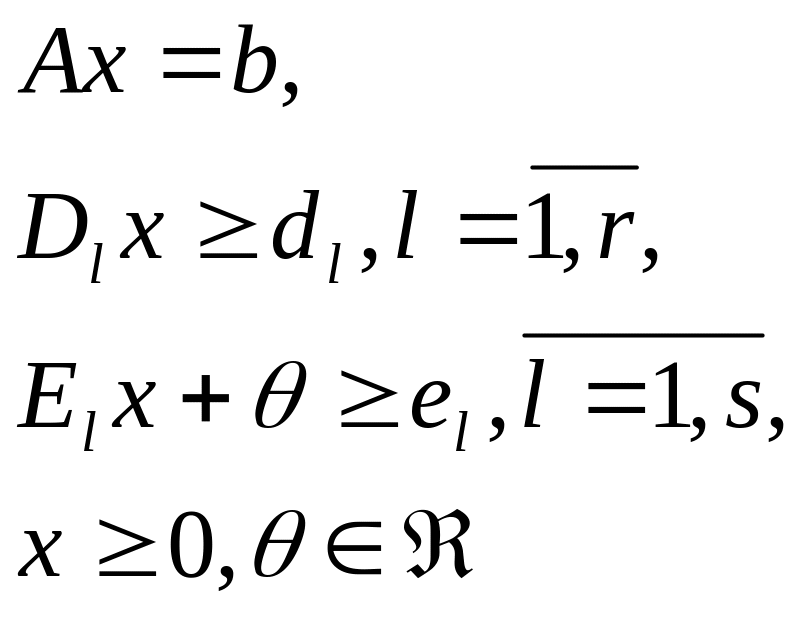
(Если условия на пока не наложены, то полагаем и не учитываем его при решении задачи для .)

Переходим к шагу 2.

Шаг 2 (проверка допустимости субоптимального решения).

Для

решаем ЗЛП

при ограничениях

Если , то

Добавляем к задаче шага 1 условие

, где , , - решение двойственной ЗЛП.

Переходим к шагу 1.

Иначе считаем для следующего

Когда для всех будет , переходим к шагу 3.

Шаг 3 (проверка оптимальности полученного решения).

Для

решаем ЗЛП

при ограничениях

Вычисляем – решение двойственной ЗЛП.

Вычисляем величины , .

Если , то

Остановить процесс решения. Оптимальное решение найдено.

Иначе

Добавить в ЗЛП шага 1 условие

Переходим к шагу 1.