Геометрические векторы. Линейные операции над ними. Коллинеарность.

Вектор АВ – направленный отрезок, А-начало, В-конец.

Каждый вектор имеет свою длину

Если начало и конец точки совпадают => нуль-вектор, направления нет.

Вектора равны, если они лежат на // прямых, имеют равную длину и направление.

Под вектором можно понимать множество равных ему векторов в различных точках пространства.

- закрепленный вектор противоположен ,

О перации над векторами: Сложение:

У множение:

Вычитание:

Два вектора называются коллинеарными, если они лежат на параллельных прямых.

Три вектора называются компланарными, если они лежат в параллельных плоскостях.

Линейная зависимость и независимость векторов. Компланарность. Зависимость 4-х векторов в пространстве.

Система векторов называется линейно-независимой, если равенство выполняется лишь в том случае, когда все числа и .

Система векторов называется линейно-зависимой, если равенство выполнимо хотя бы при одном .

Для того, чтобы два вектора были линейно-зависимы необходимо и достаточно, что бы они были коллинеарны.

Для того, чтобы три вектора были линейно-зависимы необходимо и достаточно, чтобы они были компланарны.

Векторы компланарны если они лежат в одной плоскости.

Любые 4 вектора – линейно зависимы.

Базис. Разложение по базису. Координаты вектора.

Б азис – система векторов - линейно-независима.

- разложение по базису.

Во множестве векторов в трехмерном пространстве

базис состоит из трех некомпланарных векторов.

Некоторые приложения вектора удобно задавать через направляющие косинусы:

Для реального вектора независимыми являются только два любых угла из трех.

Линейные операции над векторами в координатной форме.

1. Сложение:

2. Умножение: При умножении вектора на число каждая координата умножается на это число.

Координаты коллинеарных векторов пропорциональны.

Для каждого вектора координаты определяются однозначно.

Два вектора равны, если у них совпадают координаты.

Система ортогональная если векторы-базисы взаимно перпендикулярны.

Система ортонормированная если базисом являются ортогональные векторы

Проекция вектора на ось и ее свойства

Проекция на ось равна .

Если -тупой, то проекция будет <0.

В ортогональной системе координат длина вектора находится по теореме Пифагора:

Декартова прямоугольная система координат

Прямоугольная (декартова) система координат на

плоскости определяется заданием двух взаимно перпендикулярных прямых с общим началом и одинаковой масштабной ед. на осях.

Прямоугольная (декартова) система координат в пространстве определяется заданием трех взаимно перпендикулярных прямых с общей точкой пересечения и одинаковой масштабной ед. на осях.

В ДПСК координаты вектора имеют геометрическую иллюстрацию.

Скалярное произведение векторов, его свойства.

Скалярным произведением двух векторов называется произведение длин двух векторов на косинус угла между ними.

Свойства:

Приложения:

Скалярное произведение в координатной форме

Декартовая прямоугольная система координат:

Доказательство:

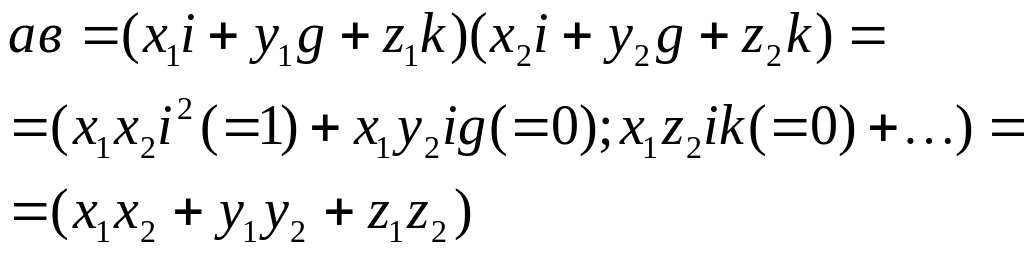
Векторное произведение векторов, его свойства

Векторным произведением двух векторов a и b обозначаемым [a,b] называется вектор с удовлетворяющий след. требованиям:

- правая тройка

Длина векторного произведения векторов равна площади параллелограмма построенного на этих векторах.

Приложения:

Векторное произведение в координатной форме

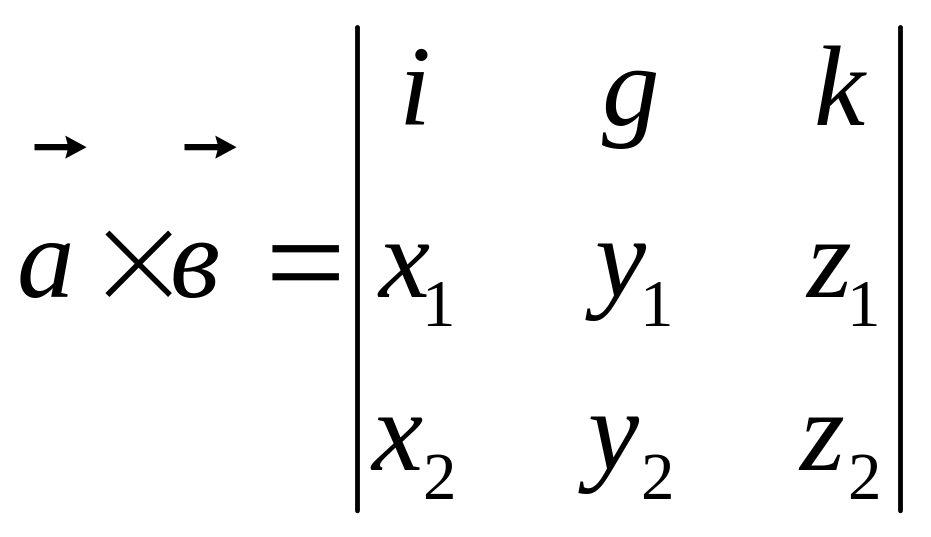
Смешанное произведение векторов, его свойства

Смешанное произведение в координатной форме

Прямая на плоскости

Ах+By+C=0 – общее уравнение прямой, где A, B одновременно не равны нулю.

А(х-х₀)+В(у-у₀)=0 – имеет ясный геометрический смысл.

Каноническое уравнение прямой:

Уравнение прямой, проходящей через две точки:

Параметрическое уравнение прямой:

t – мера расстояния от т.

Уравнение прямой с угловым коэффициентом:

Нормированное уравнение прямой:

Расстояние от точки до прямой на плоскости

М₀(х₀;у₀); L: Ах+Ву +С=0

Угол между прямыми:

L₁: А₁х+В₁у+С₁=0 L₂: А₂х+В₂у+С₂=0

n₁(А₁;В₁) n₂(А₂;В₂)

Если:

_____________________________________________________________________________________________

______________________________________________________________

L₁: Ах+Ву+С=0 n(А;В)

а(l;m)

______________________________________________________________

L₁: у = к₁х+в

L₂: у = к₂х+в

Плоскость в пространстве

Уравнение плоскости в пространстве – алгебраическое уравнение 1-й степени относительно 3-х переменных Ах+Ву+Сz+Д=0

А(х-х₀)+В(у-у₀)+С(z-z₀)=0

Угол между плоскостями

Угол между плоскостями определяется как угол между их нормалями.

Р₁: А₁х+В₁у+С₁z+Д₁=0 Р₂: А₂х+В₂у+С₂z+Д₂=0

n₁(А₁;В1;С1) n₂(А₂;В₂;С₂)

=0 – парал., =1 - перпендикулярны

Уравнение плоскости проходящей через 3 точки

М ₁, М₂, М₃.

М₁(х₀;у₀;z₀)

М₁М₂(х₁;у₁;z₁)

М₁М₃(х₂;у₂;z₂)

Расстояние от точки до плоскости

Р: Ах+Ву+Сz+Д=0

М₁(х₀;у₀;z₀)

Различные виды задания прямой в пространстве

1. Как пересечение двух плоскостей:

2. Каноническое уравнение прямой:

3. Параметрическое уравнение прямой:

4. Уравнение прямой, проходящей через две точки:

Взаимное расположение прямых в пространстве

- можно решить систему из 4-х уравнений. Если она имеет одно решение => прямые пересекаются.

Угол между прямыми находится как угол между направляющими векторами.

Взаимное расположение прямой и плоскости в пространстве

Р: Ах+Ву+Сz+Д=0

1. L // P =>

2.

3.

Кривые 2-го порядка. Эллипс.

Эллипс - геометрическое место точек на плоскости, для которых сумма расстояния до фиксированных точек (фокусы) есть величина постоянная = 2а.

Каноническое уравнение эллипса: ; a,b – полуоси эллипса

,

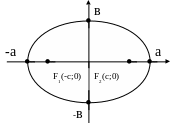Директрисы:

Гипербола

Гипербола – ГМТ на плоскости, для которых модуль разеости расстояний до 2 фиксированных точек F₁ и F₂ есть постоянная величина = 2a.

К аноническое уравнение гиперболы:

,

Директрисы:

Парабола

Р асстояние от вершины параболы до фокуса равно расстоянию от вершины до директрисы.

Каноническое уравнение параболы:

Общее уравнение кривых второго порядка через эксцентриситет

Кривая является кривой второго порядка на плоскости, если отношение расстояния от любой точки кривой до фокуса к расстоянию до соответствующей директрисы есть постоянная величина

Отношение расстояния от т. М (принадлежит графику) до фокуса к расстоянию до директрисы есть величина постоянная.

Полярные координаты

П, Э, правая ветвь Г: = , левая ветвь Г: =

Касательные к кривым второго порядка

Гипербола:

Парабола:

Эллипс:

Формулы преобразования координат при параллельном переносе и повороте

-при парал. переносе

- при повороте на угол

Кривые второго порядка со смещенным центром

Гипербола:

Эллипс:

Парабола:

Оптические свойства кривых второго порядка

Э: луч света, выпущенный из F₁ после отражения пройдет через F₂

Г: Луч света, выпущенный из F₁ после отражения пойдет по прямой, проходящей через F₂

П: Луч света, выпущенный из F, после отражения пойдет параллельно оси параболы

Общее уравнение поверхностей второго порядка. Эллипсоид

У равнение вида определяет поверхность второго

порядка в пространстве.

Эллипсоид:

Гиперболоид

Параболоид

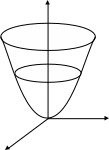
z = 0

Конус. Цилиндры второго порядка

- Эллиптический цилиндр

- Гиперболический цилиндр

- Параболический цилиндр

Нахождение линии пересечения двух поверхностей

Уравнение линии пересечения двух поверхностей находится путем решения системы уравнений, содержащей уравнения пересекающихся поверхностей. ; F₁= F_2, выражаем неизвестные.

Свойства алгебраических дополнений матрицы

Сумма произведений элементов любой строки на соответствующее алгебраическое дополнение другой строки = 0.

Матрицы. Примеры. Операции над матрицами и их свойства.

Опр. Матрица – под числовой матрицей понимается совокупность чисел, записанных в виде: , где m – строки, n – столбцы. Примеры: N – нулевая матрица, E – единичная матрица, D – диагональная матрица, T - треугольная матрица. По определению считается что A=B, если они одного размера и в них равны соответствующие элементы, т.е. , А=В, A=(a_ij). Операции над матрицами.

I.Сложение матриц:

II. Умножение матрицы на число:

III. Транспонирование матриц:

Свойства:

1. А+В=В+А, 2.(А+В)+С=А+(В+С), 3. ,

4. ,

5. , 6. (А+В)^T=А^Т+В^Т,

7. . IV. Умножение матриц друг на друга:

c_ij – сумма попарных произведений, на месте ij стоит сумма произведений соответствующих элементов i-той строки матрицы А и j-того столбца матрицы В. Свойства: 1.

2. A*(B+C)=A*B+A*C,

3. ,

4.

5.. Замечание: Данное умножение матриц удобно при работе с системами линейных уравнений, зная умножение матриц, любую систему лин. уравнений, можно переписать в матричном виде. Замечание: Деление матриц не существует, есть умножение матриц на обратную мавтрицу.