№6. Интервальный прогноз на основе линейного уравнения регрессии

В прогнозных расчетах по уравнению регрессии определяется предсказываемое y_r значение как точечный прогноз при x_р = x_k. т.е. путем подстановки в линейное уравнение регрессии = a + b  x соответствующего значения x. Однако точечный прогноз явно нереален, поэтому он дополняется расчетом стандартной ошибки , т.е. и соответственно мы получаем интервальную оценку прогнозного значения y^*:

.

Отсюда следует, что стандартная ошибка зависит от ошибки и ошибки коэффициента регрессии b, т.е.

(2.23)

Из теории выборки известно, что . Используя в качестве оценки ² остаточную дисперсию на одну степень свободы S², получим формулу расчета ошибки среднего значения переменной y:

. (2.24)

Ошибка коэффициента регрессии, как уже было показано, определяется формулой

.

Считая, что прогнозное значение фактора x_p = x_k, получим следующую формулу расчета стандартной ошибки предсказываемого по линии регрессии значения, т.е. :

. (2.25)

Соответственно имеет выражение:

. (2.26)

Рассмотренная формула стандартной ошибки предсказываемого среднего значения y при заданном значении x_k характеризует ошибку положения линии регрессии. Величина стандартной ошибки достигает минимума при x_k = x и возрастает по мере того, как «удаляется» от x в любом направлении. Иными словами, чем больше разность между x_k и x, тем больше ошибка , с которой предсказывается среднее значение y для заданного значения x_k. Можно ожидать наилучшие результаты прогноза, если признак-фактор x находится в центре области наблюдения x и нельзя ожидать хороших результатов прогноза при удалении x_k от x. Если же значение x_k оказывается за пределами наблюдаемых значений, используемых при построении линейной регрессии, то результаты прогноза ухудшаются в зависимости от того, насколько x_k откланяется от области наблюдаемых значений фактора x.

Однако фактические значения y варьируют около среднего значения . Индивидуальные значения y могут отклоняться от на величину случайной ошибки , дисперсия которой оценивается как остаточная дисперсия на одну степень свободы S. Поэтому ошибка предсказываемого индивидуального значения y должна включать не только стандартную ошибку , но и случайную ошибку S.

Средняя ошибка прогнозируемого индивидуального значения y составит:

(2.27)

При прогнозировании на основе уравнения регрессии следует помнить, что величина прогноза зависит не только от стандартной ошибки индивидуального значения у, но и от точности прогноза значения фактора x. Его величина может задаваться на основе анализа других моделей исходя из конкретной ситуации, а также анализа динамики данного фактора.

Рассмотренная формула средней ошибки индивидуального значения признака может быть использована также для оценки существенности различия предсказываемого значения и некоторого гипотетического значения.

№7

Различают два класса нелинейных регрессий:

– регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам;

– регрессии, нелинейные по оцениваемым параметрам.

Примером нелинейной регрессии по включенным в нее объясняющим переменным могут служить следующие функции:

– полиномы разных степеней:

– равносторонняя гипербола

К нелинейным регрессиям по оцениваемым параметрам относятся функции:

– степенная

– показательная

– экспоненциальная

При выборе вида зависимости между двумя признаками нагляден графический метод, особенно для монотонных (не имеющих максимумы и минимумы) зависимостей.

Таблица 2.3. – Основные зависимости и параметры для их выбора

№	Формула	Xk	Yk	Приведение к линейному виду
1				U = A + bZ; U = lgY; A = lga; Z = lgX
2				U = A + BX; U = lgY; A = lga; B = lgb
3				U = a + bX; U = 1/Y
4				Y = a + bZ; Z = lgX
5				Y = a + bZ; Z = 1/X
6				U = A + BZ; U = 1/Y; Z = 1/X; A = 1/a; B = b/a

Рассмотрим нелинейные регрессии по оцениваемым параметрам. Пусть в результате наблюдения получен ряд изучаемого показателя X и Y. По этим значениям можно построить график.

X	x1	x2	…	xn
Y	y1	y2	…	yn

Теперь необходимо подобрать формулу, которая могла бы описать экспериментальные данные. Для выбора вида зависимости воспользуемся методом средних точек. Для каждой зависимости рассчитываем координаты средних точек X_k и Y_k по формулам из таблицы. Средние точки наносим на график и выбираем ту формулу, средняя точка которой лежит ближе всего к экспериментальной кривой.

Затем необходимо определить параметры выбранной зависимости a и b таким образом, чтобы расчетная кривая лежала как можно ближе к экспериментальной кривой. В качестве критерия близости S выбираем минимум суммы квадратов отклонений между экспериментальными и расчетными значениями.

. (2.28)

Для каждой формулы в этом критерии будут присутствовать разные переменные в зависимости от приведения их к линейному виду. Например, для первой формулы U = lgY; Z = lgX. Тогда система нормальных уравнений для определения параметров линейной зависимости будет иметь вид:

,

где [Z] = Z_i; [U] = U_i; [Z²] = Z_iZ_i; [UZ] = U_iZ_i; n – количество экспериментов; A = lga и b – искомые коэффициенты уравнения (для определения а необходимо выполнить обратное преобразование: a = 10^A).

Для нахождения соответствующих сумм в каждом случае необходимо получить различные вспомогательные таблицы с учетом приведения выражений к линейному виду. Например, для второй формулы иZ_i = X_i, а U_i = lg(Y_i) и т.д.

Решив эту систему, получаем искомые значения параметров. Следует отметить, что при нахождении параметров других зависимостей необходимо сначала привести их к линейному виду согласно

Для проверки правильности выполненных действий получаем расчетные значения подстановкой в найденную формулу экспериментальных значений X. Полученные расчетные значения наносим на график с экспериментальными данными и делаем вывод об адекватности.

X	x1	x2	…	xn
Y	y1р	y2р	…	ynр

№8

Парабола второй степени целесообразна к применению, если для определенного интервала значений фактора меняется характер связи рассматриваемых признаков: прямая связь изменяется на обратную или обратная на прямую. В этом случае определяется значение фактора, при котором достигается максимальное (или минимальное) значение результативного признака: приравниваем к нулю первую производную параболы второй степени:

= а + b  x + c  x²

т.е. b + 2  c  x = 0 и x = – b/2c.

Если же исходные данные не обнаруживают изменения направленности связи, то параметры параболы второго порядка становятся трудно интерпретируемыми, а форма связи часто заменяется другими нелинейными моделями.

Применение МНК для оценки параметров параболы второй степени приводит к следующей системе нормальных уравнений:

,

Решить ее относительно параметров а, b, с можно методом определителей:

; ; ,

где  – определитель системы; a, b, c – частные определители для каждого из параметров.

При b > 0 и с < 0 кривая симметрична относительно высшей точки, т. е. точки перелома кривой, изменяющей направление связи, а именно рост на падение.

Ввиду симметричности кривой параболу второй степени далеко не всегда можно использовать в конкретных исследованиях. Чаще исследователь имеет дело лишь с отдельными сегментами параболы, а не с полной параболической формой. Кроме того, параметры параболической связи не всегда могут быть логически истолкованы. Поэтому если график зависимости не демонстрирует четко выраженной параболы второго порядка (нет смены направленности связи признаков), то она может быть заменена другой нелинейной функцией, например степенной.

Таблица 2.5. Зависимость урожайности озимой пшеницы от количества внесенных удобрений

Внесено удобрений, ц/га, x	Урожайность, ц/га, y	x2	x3	x4	yx	yx2
1	6	1	1	1	6	6	6,2
2	9	4	8	16	18	36	8,5
3	10	9	27	81	30	90	10,4
4	12	16	64	256	48	192	11,9
5	13	25	125	625	65	325	13,0
 = 15	50	55	225	979	167	649

система нормальных уравнений составит:

.

Решив эту систему методом определителей, получим:

 = 700, a = 2380, b = 2090, c = – 150.

Откуда параметры искомого уравнения составят: a = 3,4; b = 2,986; c = –0,214, а уравнение параболы примет вид:

= 3,4 + 2,986  x – 0,214  x².

Последовательно подставляя в это уравнение значения x, найдем теоретические значения

Сумма квадратов отклонений остаточных величин  (y – )² = 0,457. Ввиду того, что данные табл.2.4 демонстрируют лишь сегмент параболы второго порядка, рассматриваемая зависимость может быть охарактеризована и другой функцией.

№9

Уравнение нелинейной регрессии, так же как и в линейной зависимости, дополняется показателем корреляции, а именно индексом корреляции (R)

(2.29)

где ²_ост – остаточная дисперсия, определяемая из уравнения регрессии f(x); ²_y – общая дисперсия результативного признака.

Поскольку ²_y = (1/n)  (y – )², а ²_ост = (1/n)  (y – )², индекс корреляции можно выразить как

.

Величина данного показателя находится в границах: 0  R  1; чем ближе к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии.

Разделив остаточную сумму квадратов на соответствующее ей число степеней свободы, получим средний квадрат отклонений или дисперсию на одну степень свободы S² и вытекающую из нее стандартную ошибку S.

.

Парабола второй степени, как и полином более высокого порядка, при линеаризации принимает вид уравнения множественной регрессии. Если же нелинейное относительно объясняемой переменной уравнение регрессии при линеаризации принимает форму линейного уравнения парной регрессии, то для оценки тесноты связи может быть использован линейный коэффициент корреляции, величина которого в этом случае совпадает с индексом корреляции r_yz, где преобразованная величина признака-фактора, например, z = 1/x или z = ln x.

Приведем в качестве примера равностороннюю гиперболу y_x = a + b/x. имеем линейное уравнение y_z = a + b  z, для которого может быть определен линейный коэффициент корреляции: b  _z/_y. Возводя данное выражение в квадрат, получим:

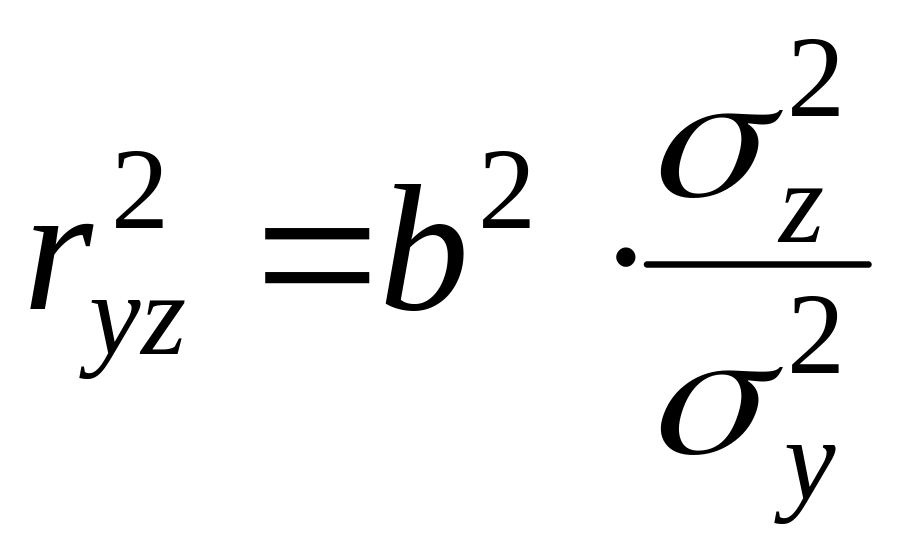, (2.30)

где и .

Отсюда r²_yz можно записать как:

. (2.31)

Как было показано в разд.2.3, и соответственно

.

Но так как и , то

,

т.е. пришли к формуле индекса корреляции:

.

Заменив z на 1/x,получим y_z = y_x, соответственно r_yz = R_yx.

Аналогичные выражения можно получить и для полулогарифмической кривой y_x = a + b  ln x, ибо в ней, как и в предыдущем случае, преобразования в линейный вид (z = ln x) не затрагивают зависимую переменную, и требование МНК (y – )²  min выполнимо.

Поскольку в расчете индекса корреляции используется соотношение факторной и общей суммы квадратов отклонений, R² имеет тот же смысл, что и коэффициент детерминации. В специальных исследованиях величину R² для нелинейных связей называют индексом детерминации.

Оценка статистической значимости индекса корреляции проводится так же, как и оценка значимости коэффициента корреляции

Индекс детерминации R² используется для проверки статистической значимости в целом уравнении нелинейной регрессии по F-критерию Фишера.

, (2.35)

где n – число наблюдений; m – число параметров при переменных x.

Величина m характеризует число степеней свободы для факторной суммы квадратов, а (n – m – 1) – число степеней свободы для остаточной суммы квадратов.

. В противном случае проводится оценка существенности различия между R² и r², вычисленных по одним и тем же исходным данным, через Стьюдента:

(2.36)

где m_{!R – r!} – ошибка разности между определяемая по формуле

(2.37)

Если t_факт > t_табл, то различия между рассматриваемыми показателями корреляции существенны и замена нелинейной регрессии уравнением линейной функции невозможна. Практически если величина t < 2, то различия между R и r несущественны, и, следовательно, возможно применение линейной регрессии, даже если есть предположения о некоторой нелинейности рассматриваемых соотношений признаков фактора и результата.

№10.