
- •Тема 1. Определители, матрицы, системы
- •П равила вычисления определителей второго и третьего порядка:
- •Свойства определителей:
- •Миноры и алгебраические дополнения
- •Теорема Лапласа
- •Вычисление определителей высших порядков, правило треугольника.
- •Виды матриц:
- •Основные операции с матрицами и их свойства
- •Ранг матрицы
- •Обратная матрица
- •Теорема о существовании и единственности обратной матрицы
- •Системы линейных алгебраических уравнений (основные понятия)
- •Методы решения
- •Условия применяемости методов
- •Теорема Кронекера-Капелли
- •Однородные системы
- •Фундаментальная система решений
- •Связь между однородной и неоднородной системами решений
- •Тема 2. Векторная алгебра. Аналитическая геометрия.
- •Векторная алгебра (основные понятия)
- •Действия над векторами
- •Линейная зависимость и независимость системы векторов (линейная комбинация)
- •Теоремы о единственности разложения любого вектора пространства (r2, r3)
- •Координаты, проекция вектора на ось
- •Декартова система координат
- •Скалярное произведение векторов (определение, свойства, приложение)
- •Векторное произведение векторов (определение, свойства, приложение)
- •Смешанное произведение векторов (определение, свойства, приложение)
- •Соответствие между геометрическими образами и уравнениями.
- •Плоскость в пространстве (типы уравнений, взаимное расположение)
- •Прямая на плоскости и в пространстве (типы уравнений, взаимное расположение)
- •Взаимное расположение прямой и плоскости
- •Кривые второго порядка
- •Окружность, эллипс, гипербола, парабола (вывод канонического уравнения, исследование кривой)
- •Преобразование системы координат на плоскости (параллельный перенос, поворот)
- •6 Основных типов поверхностей второго порядка
- •С истемы координат
- •Тема 3. Элементы линейной алгебры.
- •Линейное пространство (определение, примеры)
- •Линейная зависимость и независимость системы векторов (линейная комбинация)
- •Базис. Координаты.
- •Изменение координат при замене базиса (матрица перехода)
- •Определение скалярного произведения в линейном пространстве
- •Евклидово пространство (определение, примеры)
- •Неравенство Коши-Буняковского
- •Ортонормированный базис и его построение. Процесс ортогонализации.
- •Линейный оператор и его матрица
- •Зависимость матрицы от базиса
- •Собственные значения и вектора линейного оператора, их зависимость
- •Матрица линейного оператора в базисе из собственных векторов
- •Условия существования базиса из собственных векторов
- •Примеры операторов
- •Квадратичные формы
- •Упрощение общего уравнения линий и поверхностей второго порядка. Приведение их к каноническому виду
- •Тема 4. Введение в анализ
- •Комплексные числа (формы записи, основные операции)
- •Переменные и постоянные величины, множества (основные понятия)
- •Функция (определение, способы задания, свойства)
- •Предел числовой последовательности
- •Предел функции, геометрическая интерпретация
- •У равнения касательной и нормали
- •Гиперболические функции
- •Понятие дифференцируемой функции
- •Формула тейлора
- •Наибольшее и наименьшее значение функции
Взаимное расположение прямой и плоскости
Взаимное расположение прямой и плоскости
Плоскость
![]() и
прямая
и
прямая
![]()
1)
пересекаются
![]()
2)
прямая лежит в плоскости
![]()
3)
параллельны
![]()
Е сли
сли
![]() то случаи 1 - 3 имеют место, когда:
то случаи 1 - 3 имеют место, когда:
1)
![]()
2)
![]()
3)
![]()
Необходимое
и достаточное условие параллельности
прямой и плоскости
![]()
Угол
между прямой и плоскостью

Точка
пересечения прямой с плоскостью
![]() где
где
![]()
Уравнения
прямой, проходящей через точку
![]() перпендикулярно к плоскости
перпендикулярно к плоскости
![]() :
:
![]()
![]()
![]()
Кривые второго порядка
Алгебраической кривой второго порядка называется кривая, уравнение которой в декартовой системе координат имеет вид Ax2+2Ичн+Сy2+Dx+Ey+F=0, где не все коэффициенты А, В, С равны одновременно нулю (в противном случае кривая – прямая, т.е. кривая первого порядка).
В общем
случае может оказаться, что уравнение
определяет так называемую вырожденную
кривую (пустое множество, точку, прямую).
Если же кривая невырожденная, то для
нее найдется такая декартовая прямоугольная
система координат, в которой уравнение
этой кривой имеет один из следующих
трех видов (каноническое уравнение):
![]() ,
кривая называется эллипсом, гиперболой
или параболой, а система координат
называется канонической для заданной
кривой.
,
кривая называется эллипсом, гиперболой
или параболой, а система координат
называется канонической для заданной
кривой.
Окружность, эллипс, гипербола, парабола (вывод канонического уравнения, исследование кривой)
Окружность радиуса R с центром в
начале координат:
![]() Уравнение касательной к окружности в
произвольной точке
Уравнение касательной к окружности в
произвольной точке![]() Параметрические
уравнения:
Параметрические
уравнения:
![]() Окружность радиуса R с центром в точке
C(a; b):
Окружность радиуса R с центром в точке
C(a; b):
![]()
Эллипс – множество точек на плоскости, находящихся на данном расстоянии (≠0) от двух заданных точек.
П усть
на плоскости заданы две точки
усть
на плоскости заданы две точки
![]() и
и
![]()
![]() и дано число a (a > c). Эллипс - множество
точек M плоскости, для каждой из которых
сумма расстояний от точек
и
равна 2a. Точки
и
называются фокусами эллипса;
и дано число a (a > c). Эллипс - множество
точек M плоскости, для каждой из которых
сумма расстояний от точек
и
равна 2a. Точки
и
называются фокусами эллипса;
![]() - большая ось;
- большая ось;
![]() - малая ось; O - центр;
- малая ось; O - центр;
![]() - левый и правый фокусы;
- левый и правый фокусы;
![]() - вершины;
- вершины;
![]() - фокальные радиусы;
- фокальные радиусы;
С – фокусное расстояние,
![]() Каноническое уравнение:
Каноническое уравнение:

Эксцентриситет:
 Уравнения
директрис:
Уравнения
директрис:
![]()
Параметрические уравнения эллипса:
![]() Площадь, ограниченная эллипсом:
Площадь, ограниченная эллипсом:
![]()
О бозначим
фокусы эллипса буквами
бозначим
фокусы эллипса буквами
![]() и
и
![]() .
Расстояние между ними - фокальное
расстояние
.
Расстояние между ними - фокальное
расстояние
![]() ,
,
![]() и
и
![]() .
Если
.
Если
![]() - произвольная точка эллипса, то по
определению эллипса
- произвольная точка эллипса, то по
определению эллипса
![]() -
характеристическое уравнение эллипса.
-
характеристическое уравнение эллипса.
Введем систему координат:
![]() ,
,
![]() и
и
![]() .
Тогда фокусами будут точки
.
Тогда фокусами будут точки
![]() и
и
![]() .
.
Пусть
- любая точка эллипса, тогда
![]()
![]()
Запишем характеристическое уравнение
эллипса в координатной форме:
![]()
Преобразуем равенство:
![]() ,
,![]()
Перенесем в левую часть равенства
выражение, содержащее корень:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
,
,
![]() ,
,
![]() ,
,
![]() -
каноническое уравнение эллипса.
-
каноническое уравнение эллипса.
Гипербола – множество точек на плоскости, для которых абсолютное значение разности расстояний до двух заданных точек есть величина постоянная (≠0).
П усть
на плоскости заданы две точки
и
и дано число a (0 < a < c).
усть
на плоскости заданы две точки
и
и дано число a (0 < a < c).  и
называются
фокусами гиперболы;
- действительная ось;
-
мнимая ось;
и
называются
фокусами гиперболы;
- действительная ось;
-
мнимая ось;
![]() -
вершины;
- фокальные радиусы:
-
вершины;
- фокальные радиусы:
![]() Каноническое
уравнение:
Каноническое
уравнение:
 Эксцентриситет:
Эксцентриситет:
 Уравнения
директрис:
Уравнения
асимптот:
Уравнения
директрис:
Уравнения
асимптот:
 Уравнение гиперболы, сопряженной данной
Уравнение гиперболы, сопряженной данной
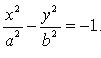 Параметрические уравнения гиперболы:
Параметрические уравнения гиперболы:
![]() Пусть
Пусть
![]() — произвольная точка гиперболы. Тогда
согласно определению гиперболы
— произвольная точка гиперболы. Тогда
согласно определению гиперболы
![]() или
или
![]() ,
т.е.
,
т.е.
![]() .
После упрощений, как это было сделано
при выводе уравнения эллипса, получим
каноническое уравнение гиперболы
.
После упрощений, как это было сделано
при выводе уравнения эллипса, получим
каноническое уравнение гиперболы
П арабола
– множество точек на плоскости, для
которых расстояние до заданной точки
и до заданной прямой – величина
постоянная. Расстояние от фокуса F до
директрисы называется параметром
параболы и обозначается через p (p > 0).
арабола
– множество точек на плоскости, для
которых расстояние до заданной точки
и до заданной прямой – величина
постоянная. Расстояние от фокуса F до
директрисы называется параметром
параболы и обозначается через p (p > 0).
Д ля
вывода уравнения параболы выберем
систему координат Оху так, чтобы ось Ох
проходила через фокус F перпендикулярно
директрисе в направлении от директрисы
к F, а начало координат О расположим
посередине между фокусом и директрисой
(см. рис. 60). В выбранной системе фокус F
имеет координаты,
ля
вывода уравнения параболы выберем
систему координат Оху так, чтобы ось Ох
проходила через фокус F перпендикулярно
директрисе в направлении от директрисы
к F, а начало координат О расположим
посередине между фокусом и директрисой
(см. рис. 60). В выбранной системе фокус F
имеет координаты,
![]() а уравнение директрисы имеет вид
а уравнение директрисы имеет вид
![]() .
Пусть
— произвольная точка параболы. Соединим
точку Μ с F. Проведем отрезок ΜΝ
перпендикулярно директрисе. Согласно
определению параболы MF = ΜΝ. По формуле
расстояния между двумя точками находим:
.
Пусть
— произвольная точка параболы. Соединим
точку Μ с F. Проведем отрезок ΜΝ
перпендикулярно директрисе. Согласно
определению параболы MF = ΜΝ. По формуле
расстояния между двумя точками находим:
 Следовательно,
Следовательно,
![]() Возведя обе части уравнения в квадрат,
получим
Возведя обе части уравнения в квадрат,
получим
![]()
![]() .
Уравнение называется каноническим
уравнением параболы.
.
Уравнение называется каноническим
уравнением параболы.
