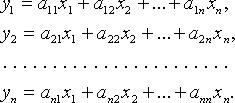- •Тема 1. Определители, матрицы, системы
- •П равила вычисления определителей второго и третьего порядка:
- •Свойства определителей:
- •Миноры и алгебраические дополнения
- •Теорема Лапласа
- •Вычисление определителей высших порядков, правило треугольника.
- •Виды матриц:
- •Основные операции с матрицами и их свойства
- •Ранг матрицы
- •Обратная матрица
- •Теорема о существовании и единственности обратной матрицы
- •Системы линейных алгебраических уравнений (основные понятия)
- •Методы решения
- •Условия применяемости методов
- •Теорема Кронекера-Капелли
- •Однородные системы
- •Фундаментальная система решений
- •Связь между однородной и неоднородной системами решений
- •Тема 2. Векторная алгебра. Аналитическая геометрия.
- •Векторная алгебра (основные понятия)
- •Действия над векторами
- •Линейная зависимость и независимость системы векторов (линейная комбинация)
- •Теоремы о единственности разложения любого вектора пространства (r2, r3)
- •Координаты, проекция вектора на ось
- •Декартова система координат
- •Скалярное произведение векторов (определение, свойства, приложение)
- •Векторное произведение векторов (определение, свойства, приложение)
- •Смешанное произведение векторов (определение, свойства, приложение)
- •Соответствие между геометрическими образами и уравнениями.
- •Плоскость в пространстве (типы уравнений, взаимное расположение)
- •Прямая на плоскости и в пространстве (типы уравнений, взаимное расположение)
- •Взаимное расположение прямой и плоскости
- •Кривые второго порядка
- •Окружность, эллипс, гипербола, парабола (вывод канонического уравнения, исследование кривой)
- •Преобразование системы координат на плоскости (параллельный перенос, поворот)
- •6 Основных типов поверхностей второго порядка
- •С истемы координат
- •Тема 3. Элементы линейной алгебры.
- •Линейное пространство (определение, примеры)
- •Линейная зависимость и независимость системы векторов (линейная комбинация)
- •Базис. Координаты.
- •Изменение координат при замене базиса (матрица перехода)
- •Определение скалярного произведения в линейном пространстве
- •Евклидово пространство (определение, примеры)
- •Неравенство Коши-Буняковского
- •Ортонормированный базис и его построение. Процесс ортогонализации.
- •Линейный оператор и его матрица
- •Зависимость матрицы от базиса
- •Собственные значения и вектора линейного оператора, их зависимость
- •Матрица линейного оператора в базисе из собственных векторов
- •Условия существования базиса из собственных векторов
- •Примеры операторов
- •Квадратичные формы
- •Упрощение общего уравнения линий и поверхностей второго порядка. Приведение их к каноническому виду
- •Тема 4. Введение в анализ
- •Комплексные числа (формы записи, основные операции)
- •Переменные и постоянные величины, множества (основные понятия)
- •Функция (определение, способы задания, свойства)
- •Предел числовой последовательности
- •Предел функции, геометрическая интерпретация
- •У равнения касательной и нормали
- •Гиперболические функции
- •Понятие дифференцируемой функции
- •Формула тейлора
- •Наибольшее и наименьшее значение функции
Евклидово пространство (определение, примеры)
Действительное
линейное пространство E называется
евклидовым, если каждой паре векторов
![]() сопоставляется число (скалярное
произведение)
сопоставляется число (скалярное
произведение)![]() так, что
так, что
![]() и
и
![]() выполняются аксиомы. Можно ввести
длину вектора
выполняются аксиомы. Можно ввести
длину вектора
![]() - число.
- число.![]() С
помощью скалярного произведения можно
находить углы между векторами
С
помощью скалярного произведения можно
находить углы между векторами
![]() .
.
Наглядными примерами евклидовых пространств могут служить пространства:
размерности 1 (вещественная прямая)
размерности 2 (евклидова плоскость)
размерности 3 (евклидово трехмерное пространство)
Евклидово пространство можно считать современной интерпретацией и обобщением (так как оно допускает размерности больше трех) классической (Евклидовой) геометрии.
Более абстрактный пример:
пространство вещественных многочленов p(x) степени, не превосходящей n, со скалярным произведением, определенным как интеграл произведения по конечному отрезку (или по всей прямой, но с быстро спадающей весовой функцией, например)
Неравенство Коши-Буняковского
Для любых двух элементов
из произвольного евклидова пространства
E справедливо неравенство
![]() которое
позволяет определить угол между
ненулевыми векторами
.
Ненулевые векторы x, y
ϵ E называются
ортогональными, если (x,
y)=0
которое
позволяет определить угол между
ненулевыми векторами
.
Ненулевые векторы x, y
ϵ E называются
ортогональными, если (x,
y)=0
Для того, чтобы можно было пользоваться формулой неравенства в произвольном евклидовом пространстве E , нам надо показать, что cosφ ≤ 1 для любых векторов x,y ϵ E . Для доказательства этого утверждения рассмотрим вектор
αx - y , где α - вещественное число. В силу аксиомы при любом α квадратичная форма положительно определена, т.е.
(αx - y,αx - y)≥ 0 или α2 (x, x) - 2α(x, y) + (y, y)≥ 0. В левой части неравенства стоит квадратный трёхчлен относительно α с постоянными коэффициентами. Трёхчлен не может иметь различных вещественных корней, так как тогда он не
мог бы сохранять знака для всех значений α . Поэтому дискриминант этого многочлена не может быть положительным (x, y)2 - (x, x)(y, y)≤ 0 . Следовательно (x, y)2≤ (x, x)(y, y), откуда, извлекая квадратный корень, получаем
|(x, y)|≤ |x| |y| , что и требовалось доказать. Это неравенство называют неравенством Коши-Буняковского.
Ортонормированный базис и его построение. Процесс ортогонализации.
Векторы
ортогональны, если
![]() Система
Система![]() векторов евклидова пространства
называется ортогональной, если
векторы системы попарно ортогональны.
Ортогональная система
векторов евклидова пространства
называется ортогональной, если
векторы системы попарно ортогональны.
Ортогональная система![]() векторов n-мерного евклидова пространства
называется ортонормированной, если
все векторы системы имеют единичную
длину.
векторов n-мерного евклидова пространства
называется ортонормированной, если
все векторы системы имеют единичную
длину.
Система векторов![]() для которой
для которой![]() называется ортонормированной.
называется ортонормированной.
Во всяком пространстве
![]() существует ортонормированный базис.
Из произвольного базиса
существует ортонормированный базис.
Из произвольного базиса![]() пространства
пространства
![]() ортогональный базис может быть построен
с помощью процесса ортогонализации:
ортогональный базис может быть построен
с помощью процесса ортогонализации:
![]()
![]() где
где

![]() где
где

Пронормировав каждый вектор![]() получим ортонормированный базис. В
ортонормированном базисе (
)
для векторов
получим ортонормированный базис. В
ортонормированном базисе (
)
для векторов
![]() имеем:
имеем:

Линейный оператор и его матрица
Если каждому вектору x
поставить в соответствие по некоторому
правилу y, то мы зададим
отображение (оператор).
![]() .
Оператор будет линейным, если
.
Оператор будет линейным, если

Условия
1 и 2 равносильны соотношению
![]()
М атрица
линейного оператора
атрица
линейного оператора
![]() в базисе (
)
- матрица , столбцами которой являются
столбцы образов базисных векторов
в базисе (
)
- матрица , столбцами которой являются
столбцы образов базисных векторов
![]() оператора f, т. е.
оператора f, т. е.
![]() Если
в базисе (
)
имеет координатный столбец
Если
в базисе (
)
имеет координатный столбец
![]() - линейный оператор с матрицей A в данном
базисе,
- линейный оператор с матрицей A в данном
базисе,
![]() - координатный столбец вектора
- координатный столбец вектора
![]() , то Y = AX (употребляется также запись
, то Y = AX (употребляется также запись
![]() ). Более подробно:
). Более подробно: