22. Произведение матриц.

Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам: AB = C;

Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.

23. Матричная запись линейного преобразования и системы линейных уравнений.

Матрица линейного преобразования A: в базисе e=||e₁…e_n|| называется матрица, столбцы которой – координатные столбцы векторов A(e₁),…, A(e_n) в базисе e. Системы линейных уравнений (основной случай). мы будем называть системой m линейных уравнений с n неизвестными x¹,…, xⁿ. Коэффициенты этих уравнений мы будем записывать в виде матрицы называемой матрицей системы. Числа, стоящие в правых частях уравнений, образуют столбец b, называемый столбцом свободных членов.

24. Ассоциативность умножения матриц, транспонирование произведения матриц, умножение на единичную матрицу.

Операция перемножения матриц ассоциативна, т.е. если определены произведения АВ и (АВ)С, то определены ВС и А(ВС), и выполняется равенство: (АВ)С=А(ВС).

Если определено произведение АВ , то определено произведение В^ТА^Т и выполняется равенство: (АВ)^Т = В^ТА^Т, где индексом Т обозначается транспонированная матрица.

Матрицу В называют транспонированной матрицей А, а переход от А к В транспонированием, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы В.

А = 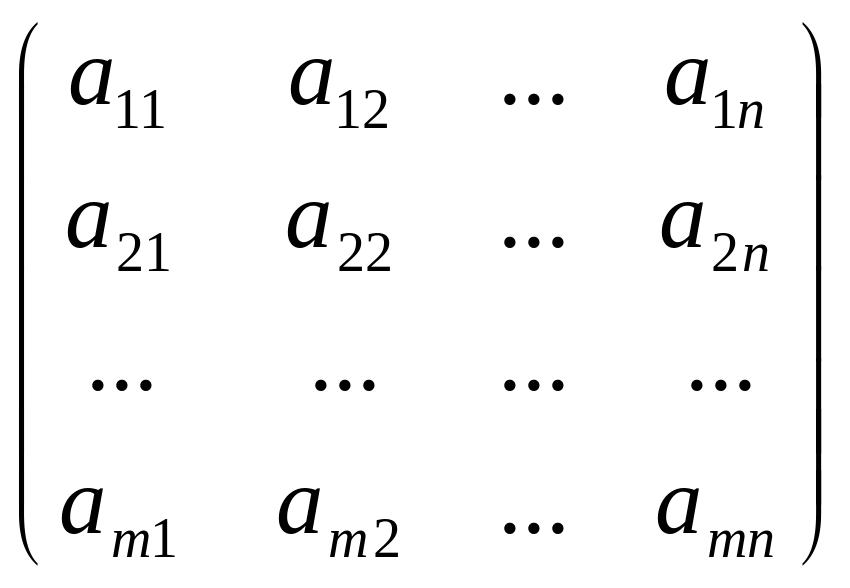; В = А^Т= ; другими словами, b_ji = a_ij.

В качестве следствия из предыдущего свойства (5) можно записать, что: (ABC)^T = C^TB^TA^T, при условии, что определено произведение матриц АВС.

A^TB =  = = ;

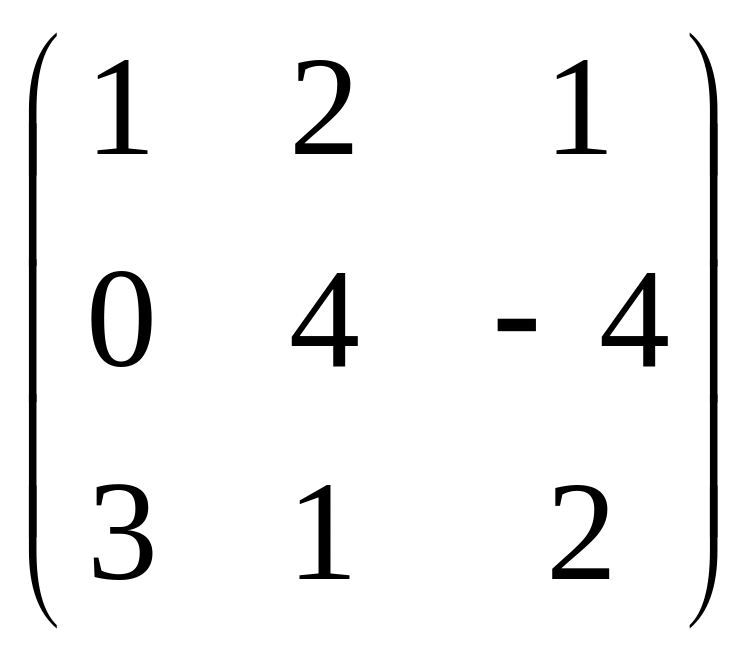
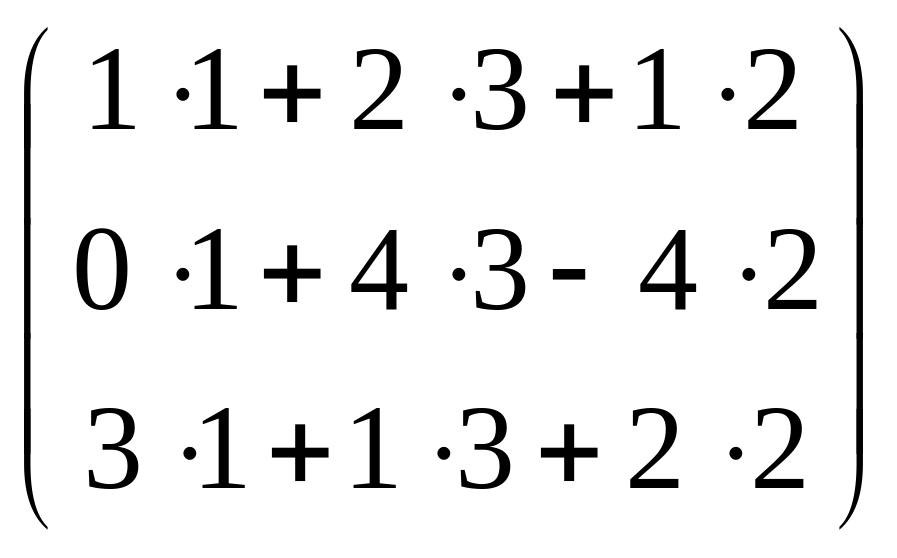25. Сложение, вычитание матриц, произведение матрицы на число.

Матрицей размера mn, где m – число строк, n – число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются a_ij, где i- номер строки, а j- номер столбца.

А =

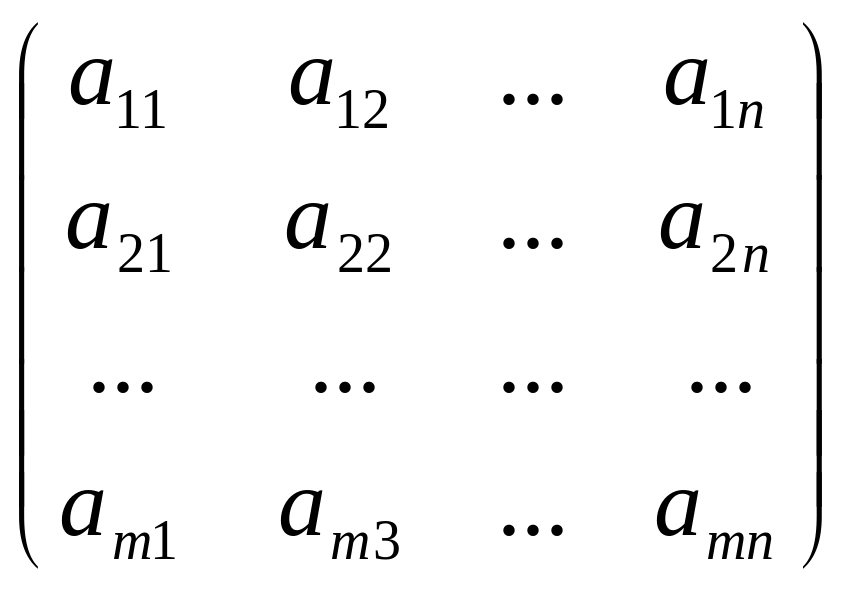
Основные действия над матрицами.

Матрица может состоять как из одной строки, так и из одного столбца. Вообще говоря, матрица может состоять даже из одного элемента. Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной.

Единичная матрица – матрица, у которой на главной диагонали стоят единицы, а остальные элементы = 0.

Если a_mn = a_nm , то матрица называется симметрической: 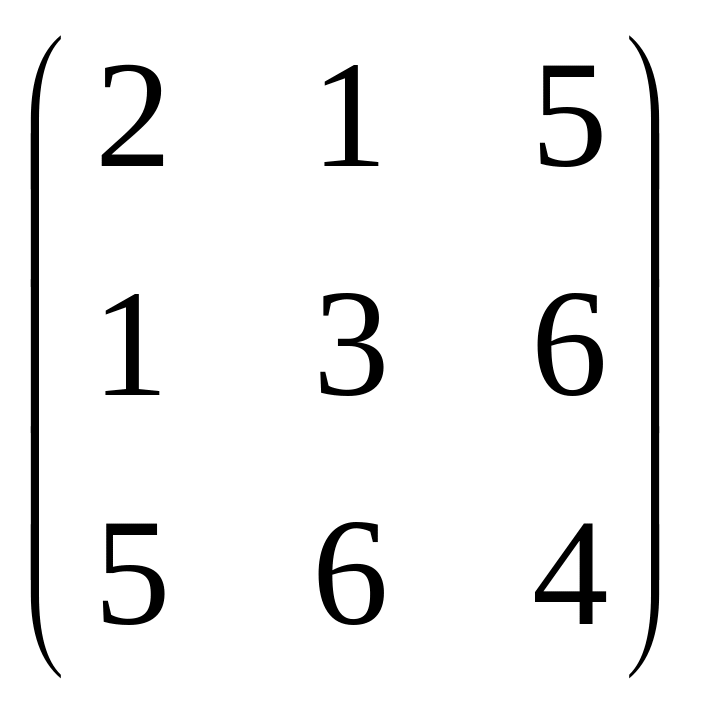- симметрическая матрица.

Квадратная матрица диагональ которой любые числа, а остальные элементы = 0 называется диагональной матрицей.

1. Сложение матриц.

Определение 3.4. Суммой матриц А и В одинаковой размерности m n называется матрица С той же размерности, каждый элемент которой равен сумме элементов матриц А и В, стоящих на тех же местах:

Свойства сложения: 1. коммунитативность сложения: А + В = В + А.

2. Ассоциативность сложения: (А + В) + С = А + (В + С) .

3. Если О – нулевая матрица, то А + О = О + А = А

Замечание 1. Справедливость этих свойств следует из определения операции сложения матриц.

Замечание 2. Отметим еще раз, что складывать можно только матрицы одинаковой размерности.