
- •Тема 1. Элементы общей алгебры
- •Комплексные числа, действия над ними.
- •Тригонометрическая форма, сопряженные числа.
- •Формула Муавра.
- •Извлечение квадратного корня, корни высших степеней,
- •Корни из единицы.
- •Многочлены одной переменной, операции над ними.
- •Алгоритм деления с остатком.
- •Делимость многочленов, ее свойства.
- •Наибольший общий делитель, алгоритм Евклида.
- •Метод Горнера.
- •Основная теорема алгебры (без док-ва).
- •Формулы Виета.
- •Тема 2. Теория определителей
- •Определители второго и третьего порядка.
- •Определители -го порядка. (определители высших порядков)
- •Перестановки, инверсии.
- •Три свойства перестановок.
- •Свойства определителей: определитель транспонированной матрицы, перемена местами строк в определителе, определитель матрицы с одинаковыми строками.
- •Свойства определителей: разложение определителя по строке.
- •Определитель ступенчатой матрицы.
- •Тема 3. Алгебра матриц
- •Линейное преобразование, умножение линейных преобразований.
- •Произведение матриц.
- •Матричная запись линейного преобразования и системы линейных уравнений.
- •Ассоциативность умножения матриц, транспонирование произведения матриц, умножение на единичную матрицу.
- •Сложение, вычитание матриц, произведение матрицы на число.
- •Сложение матриц.
- •Умножение матрицы на число.
- •Законы дистрибутивности, ассоциативность умножения на число, скалярная матрица.
- •Линейная комбинация матриц, многочлен от матрицы.
- •Сложение и умножение многочленов от матриц.
- •Обратная, неособенная, взаимная матрица.
- •Условие существования, вычисление обратной матрицы.
- •Обратная матрица для произведения матриц.
- •Решение систем линейных уравнений с помощью обратной матрицы.
- •Вычисление обратной матрицы с помощью элементарных преобразований.
- •Собственные числа и собственные столбцы матрицы.
- •Характеристический многочлен.
- •Собственные числа вещественной симметричной матрицы.
- •Теорема Гамильтона-Кэли.
- •Тема 4. Системы линейных уравнений
- •Системы линейных уравнений, их типы.
- •Теорема Крамера.
- •Ранг матрицы.
- •Элементарные преобразования матриц.
- •Вычисление ранга с помощью элементарных преобразований.
- •Метод Гаусса.
- •Элементарные преобразования систем линейных уравнений.
- •Теорема Кронекера-Капелли.
- •Теорема о числе решений системы линейных уравнений.
- •Однородные системы линейных уравнений. Общее решение однородной линейной системы.
- •Линейная комбинация решений, фундаментальная система решений.
- •Теоремы о структуре общего решения однородной и неоднородной системы линейных уравнений.
- •Тема 5. Квадратичные формы
- •Квадратичная форма, ее матрица, матричная запись квадратичной формы.
- •Тема 6. Алгебра векторов
- •Геометрический вектор, модуль вектора, коллинеарные и компланарные вектора.
- •Свободные, скользящие и связанные вектора.
- •Сумма, разность векторов, произведение вектора на число. Свойства этих операций.
- •Угол между векторами.
- •Вычисление ортогональной проекции.
- •Ортогональная проекция суммы векторов и произведения вектора на число.
- •Линейная комбинация векторов, линейно независимые вектора. Условия линейной зависимости векторов.
- •Базис, разложение вектора по базису, координаты вектора.
- •Изменение координат при сложении векторов и умножении вектора на число, координаты коллинеарных векторов.
- •Ортогональный и ортонормированный базис, направляющие косинусы.
- •Скалярное произведение векторов. Ортогональные вектора, скалярный квадрат.
- •Свойства скалярного произведения, вычисление скалярного произведения через координаты вектора.
- •Правая тройка векторов.
- •Векторное произведение векторов. Свойства векторного произведения.
- •Вычисление векторного произведения в координатах.
- •Тема 7. Метод координат
- •Декартова система координат.
- •Тема 8. Прямая и плоскость
- •Аналитическая геометрия на плоскости и в пространстве.
- •Прямая на плоскости и алгебраическая кривая первого порядка. Общее уравнение прямой.
- •Условия параллельности и перпендикулярности плоскостей.
- •Угол между прямыми.
- •Расстояние от точки до прямой.
- •Плоскость в пространстве и алгебраическая поверхность первого порядка. Общее уравнение плоскости.
- •Векторное, параметрическое, каноническое уравнение прямой.
- •Уравнение прямой в пространстве по точке и направляющему вектору.
- •Уравнение прямой, проходящей через две данные точки.
- •Угол между плоскостями.
- •Угол между прямыми в пространстве.
- •Условия параллельности и перпендикулярности прямых в пространстве.
- •Взаимное расположение прямых в пространстве (канонические и общие уравнения).
- •Взаимное расположение прямой и плоскости.
- •Угол между прямой и плоскостью.
- •Расстояние от точки до плоскости.
- •Расстояние от точки до прямой.
- •Расстояние между прямой и плоскостью.
Взаимное расположение прямой и плоскости.
Прямая может лежать на данной плоскости, быть параллельна данной плоскости или пересекать ее в одной точке, см. следующие рисунки.
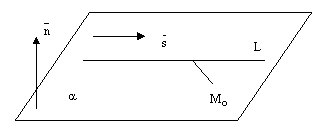
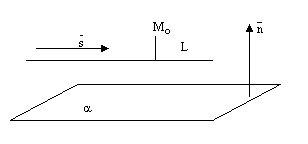
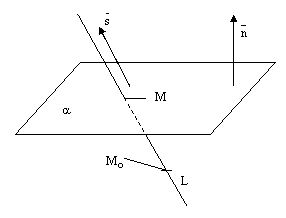
рис.6. рис.7 рис.8.
Теорема.
Пусть плоскость α задана
общим уравнением
![]() ,
а прямая L
задана каноническими уравнениями
,
а прямая L
задана каноническими уравнениями
![]() или параметрическими уравнениями
или параметрическими уравнениями
 ,
,
![]() ,
,
в
которых
![]() –
координаты нормального вектора плоскости
α,
–
координаты нормального вектора плоскости
α,
![]() –
координаты произвольной фиксированной
точки прямой L,
–
координаты произвольной фиксированной
точки прямой L, ![]() –
координаты направляющего вектора
прямой L. Тогда:
–
координаты направляющего вектора
прямой L. Тогда:
1)
если
![]() ,
то прямая L пересекает плоскость α в
точке, координаты которой
,
то прямая L пересекает плоскость α в
точке, координаты которой
![]() можно
найти из системы уравнений
можно
найти из системы уравнений
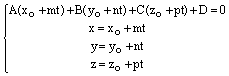 ;
(7)
;
(7)
2)
если
![]() и
и
![]() ,
то прямая лежит на плоскости;
,
то прямая лежит на плоскости;
3)
если
и
![]() ,
то прямая параллельна плоскости.
,
то прямая параллельна плоскости.
Доказательство.
Условие
![]() говорит
о том, что векторы
говорит
о том, что векторы
![]() и
и
![]() не
ортогональны, а значит прямая не
параллельна плоскости и не лежит в
плоскости, а значит пересекает ее в
некоторой точке М. Координаты точки М
удовлетворяют как уравнению плоскости,
так и уравнениям прямой, т.е. системе
(7). Решаем первое уравнение системы (7)
относительно неизвестной t и затем,
подставляя найденное значение t в
остальные уравнения системы, находим
координаты искомой точки.
не
ортогональны, а значит прямая не
параллельна плоскости и не лежит в
плоскости, а значит пересекает ее в
некоторой точке М. Координаты точки М
удовлетворяют как уравнению плоскости,
так и уравнениям прямой, т.е. системе
(7). Решаем первое уравнение системы (7)
относительно неизвестной t и затем,
подставляя найденное значение t в
остальные уравнения системы, находим
координаты искомой точки.
Если
![]() ,
то это означает, что
,
то это означает, что
![]() .
А такое возможно лишь тогда, когда прямая
лежит на плоскости или параллельна ей.
Если прямая лежит на плоскости, то любая
точка прямой является точкой плоскости
и координаты любой точки прямой
удовлетворяют уравнению плоскости.
Поэтому достаточно проверить, лежит ли
на плоскости точка
.
Если Ax0+By0+Cz0+D=0,
то точка
.
А такое возможно лишь тогда, когда прямая
лежит на плоскости или параллельна ей.
Если прямая лежит на плоскости, то любая
точка прямой является точкой плоскости
и координаты любой точки прямой
удовлетворяют уравнению плоскости.
Поэтому достаточно проверить, лежит ли
на плоскости точка
.
Если Ax0+By0+Cz0+D=0,
то точка
![]() –
лежит на плоскости, а это означает, что
и сама прямая лежит на плоскости.
–
лежит на плоскости, а это означает, что
и сама прямая лежит на плоскости.
Если , а Ax0+By0+Cz0+D≠0, то точка на прямой не лежит на плоскости, а это означает, что прямая параллельна плоскости.
Теорема доказана.
Угол между прямой и плоскостью.
Определение. Углом между прямой и плоскостью называется любой угол между прямой и ее проекцией на эту плоскость.

![]()
![]()
![]()
В
координатной форме:
![]()
Условия параллельности и перпендикулярности прямой и плоскости в пространстве.
параллельность
![]()
перпендикулярность.
![]()
Расстояние от точки до плоскости.
П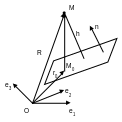 усть
дана плоскость с уравнением (r-r0,n)
= 0
и точка М
с радиус-вектором R.
Рассмотрим вектор
усть
дана плоскость с уравнением (r-r0,n)
= 0
и точка М
с радиус-вектором R.
Рассмотрим вектор
![]() ,
соединяющий начальную точку плоскости,
с M.
Расстояние от точки до плоскости равно
модулю его скалярной проекции на вектор
n,
т.е.:
,
соединяющий начальную точку плоскости,
с M.
Расстояние от точки до плоскости равно
модулю его скалярной проекции на вектор
n,
т.е.:
![]()
Если
в декартовой прямоугольной системе
координат точка М
имеет координаты (x,
y,
z)
то равенство h
записывается согласно условиям 1 и 2
так:
![]()
Условие 1: Пусть x, y, z – компоненты вектора r в общей декартовой системе координат. Тогда скалярное произведение (r-r0,n) при n≠0 записывается линейным многочленом Ax+By+Cz+D (A2+B2+C2 ≠0).
Обратно для любого многочлена найдутся такие векторы r0 и n≠0, что в заданной общей декартовой системе координат Ax+By+Cz+D=(r-r0,n).
Условие 2: Если система координат декартова прямоугольная, то вектор с компонентами А, В, С является нормальным вектором для плоскости с уравнением Ax+By+Cz+D=0.
