
- •Тема 1. Элементы общей алгебры
- •Комплексные числа, действия над ними.
- •Тригонометрическая форма, сопряженные числа.
- •Формула Муавра.
- •Извлечение квадратного корня, корни высших степеней,
- •Корни из единицы.
- •Многочлены одной переменной, операции над ними.
- •Алгоритм деления с остатком.
- •Делимость многочленов, ее свойства.
- •Наибольший общий делитель, алгоритм Евклида.
- •Метод Горнера.
- •Основная теорема алгебры (без док-ва).
- •Формулы Виета.
- •Тема 2. Теория определителей
- •Определители второго и третьего порядка.
- •Определители -го порядка. (определители высших порядков)
- •Перестановки, инверсии.
- •Три свойства перестановок.
- •Свойства определителей: определитель транспонированной матрицы, перемена местами строк в определителе, определитель матрицы с одинаковыми строками.
- •Свойства определителей: разложение определителя по строке.
- •Определитель ступенчатой матрицы.
- •Тема 3. Алгебра матриц
- •Линейное преобразование, умножение линейных преобразований.
- •Произведение матриц.
- •Матричная запись линейного преобразования и системы линейных уравнений.
- •Ассоциативность умножения матриц, транспонирование произведения матриц, умножение на единичную матрицу.
- •Сложение, вычитание матриц, произведение матрицы на число.
- •Сложение матриц.
- •Умножение матрицы на число.
- •Законы дистрибутивности, ассоциативность умножения на число, скалярная матрица.
- •Линейная комбинация матриц, многочлен от матрицы.
- •Сложение и умножение многочленов от матриц.
- •Обратная, неособенная, взаимная матрица.
- •Условие существования, вычисление обратной матрицы.
- •Обратная матрица для произведения матриц.
- •Решение систем линейных уравнений с помощью обратной матрицы.
- •Вычисление обратной матрицы с помощью элементарных преобразований.
- •Собственные числа и собственные столбцы матрицы.
- •Характеристический многочлен.
- •Собственные числа вещественной симметричной матрицы.
- •Теорема Гамильтона-Кэли.
- •Тема 4. Системы линейных уравнений
- •Системы линейных уравнений, их типы.
- •Теорема Крамера.
- •Ранг матрицы.
- •Элементарные преобразования матриц.
- •Вычисление ранга с помощью элементарных преобразований.
- •Метод Гаусса.
- •Элементарные преобразования систем линейных уравнений.
- •Теорема Кронекера-Капелли.
- •Теорема о числе решений системы линейных уравнений.
- •Однородные системы линейных уравнений. Общее решение однородной линейной системы.
- •Линейная комбинация решений, фундаментальная система решений.
- •Теоремы о структуре общего решения однородной и неоднородной системы линейных уравнений.
- •Тема 5. Квадратичные формы
- •Квадратичная форма, ее матрица, матричная запись квадратичной формы.
- •Тема 6. Алгебра векторов
- •Геометрический вектор, модуль вектора, коллинеарные и компланарные вектора.
- •Свободные, скользящие и связанные вектора.
- •Сумма, разность векторов, произведение вектора на число. Свойства этих операций.
- •Угол между векторами.
- •Вычисление ортогональной проекции.
- •Ортогональная проекция суммы векторов и произведения вектора на число.
- •Линейная комбинация векторов, линейно независимые вектора. Условия линейной зависимости векторов.
- •Базис, разложение вектора по базису, координаты вектора.
- •Изменение координат при сложении векторов и умножении вектора на число, координаты коллинеарных векторов.
- •Ортогональный и ортонормированный базис, направляющие косинусы.
- •Скалярное произведение векторов. Ортогональные вектора, скалярный квадрат.
- •Свойства скалярного произведения, вычисление скалярного произведения через координаты вектора.
- •Правая тройка векторов.
- •Векторное произведение векторов. Свойства векторного произведения.
- •Вычисление векторного произведения в координатах.
- •Тема 7. Метод координат
- •Декартова система координат.
- •Тема 8. Прямая и плоскость
- •Аналитическая геометрия на плоскости и в пространстве.
- •Прямая на плоскости и алгебраическая кривая первого порядка. Общее уравнение прямой.
- •Условия параллельности и перпендикулярности плоскостей.
- •Угол между прямыми.
- •Расстояние от точки до прямой.
- •Плоскость в пространстве и алгебраическая поверхность первого порядка. Общее уравнение плоскости.
- •Векторное, параметрическое, каноническое уравнение прямой.
- •Уравнение прямой в пространстве по точке и направляющему вектору.
- •Уравнение прямой, проходящей через две данные точки.
- •Угол между плоскостями.
- •Угол между прямыми в пространстве.
- •Условия параллельности и перпендикулярности прямых в пространстве.
- •Взаимное расположение прямых в пространстве (канонические и общие уравнения).
- •Взаимное расположение прямой и плоскости.
- •Угол между прямой и плоскостью.
- •Расстояние от точки до плоскости.
- •Расстояние от точки до прямой.
- •Расстояние между прямой и плоскостью.
Уравнение прямой, проходящей через две данные точки.
Пусть
в пространстве задана общая декартова
система координат и две точки M1
и М2,
с координатами (х1,
у1,
z2)
и
(х2,
у2,
z3).
Что бы написать уравнение прямой М1М2
примем М1
за начальную точку, а вектор
![]() за направляющих вектор. Это вектор не
нулевой, если точки не совпадают. По
формуле мы получаем:
за направляющих вектор. Это вектор не
нулевой, если точки не совпадают. По
формуле мы получаем:
![]() .
.
Если в этих равенствах какое-либо из знаменателей равен нулю, то следует приравнять нулю соответствующих числитель, в планиметрии задание решается также. Отличие только в том, что координаты точек (x1, y1) и (x2, у2), и мы получаем:
![]()
Угол между плоскостями.
Угол между плоскостями находится по формуле:
Выбор знака косинуса зависит от того, какой угол между плоскостями следует найти – острый, или смежный с ним тупой.
Угол между прямыми в пространстве.
Пусть в пространстве заданы две прямые. Их параметрические уравнения: l1:
![]() ;
l2:
;
l2:
![]() ;
;
![]()
Угол между прямыми и угол между направляющими векторами этих прямых связаны соотношением: = 1 или = 1800 - 1. Угол между направляющими векторами находится из скалярного произведения. Таким образом:
 .
.
Условия параллельности и перпендикулярности прямых в пространстве.
Чтобы
две прямые были параллельны необходимо
и достаточно, чтобы направляющие векторы
этих прямых были коллинеарны, т.е. их
соответствующие координаты были
пропорциональны.
![]()
Чтобы две прямые были перпендикулярны необходимо и достаточно, чтобы направляющие векторы этих прямых были перпендикулярны, т.е. косинус угла между ними равен нулю: m1m2+n1n2+p1p2=0.
Взаимное расположение прямых в пространстве (канонические и общие уравнения).
Взаимное расположение двух прямых и пространстве характеризуется следующими тремя возможностями.
Прямые лежат в одной плоскости и не имеют общих точек — параллельные прямые.
Прямые лежат и одной плоскости и имеют одну общую точку — прямые пересекаются.
В пространстве две прямые могут быть расположены еще так, что не лежат ни в одной плоскости. Такие прямые называются скрещивающимися (не пересекаются и не параллельны).
Т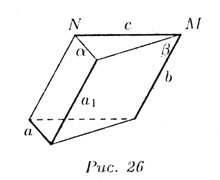 еорема.
Если одна из двух прямых лежит в некоторой
плоскости, а другая пересекает эту
плоскость в точке, которая не лежит на
первой прямой, то эти прямые скрещиваются.
еорема.
Если одна из двух прямых лежит в некоторой
плоскости, а другая пересекает эту
плоскость в точке, которая не лежит на
первой прямой, то эти прямые скрещиваются.
На рис. 26 прямая a лежит в плоскости α, а прямая с пересекает α в точке N. Прямые a и с — скрещивающиеся.
Теорема. Через каждую из двух скрещивающихся прямых проходит только одна плоскость, параллельная другой прямой.
На рис. 26 прямые a и b скрещиваются. Черен прямую а проведена плоскость α || b (в плоскости β указана прямая a1 || b).
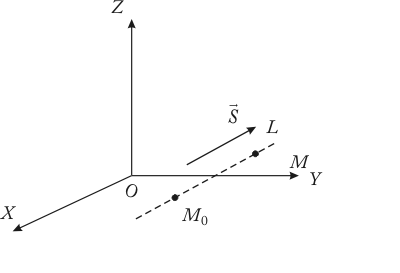
Канонические и параметрические уравнения прямой
Положение прямой L в пространстве должным образом определяется заданием т. L.
Обозначим через L (рис. 3.8).
Тогда
![]() . Рис.
3.8
. Рис.
3.8
Эти уравнения прямой L именуют каноническими. Если приравнять эти отношения параметру t и определить t, то будем иметь параметрические уравнения прямой: x=x0+mt, y=y0+nt, z=z0+pt (3.3)
В
евклидовом пространстве c ортонормированным
базисом канонические уравнения прямой
записываются как,
![]() —
направляющий вектор.
—
направляющий вектор.
Допустим
заданы две точки L.
В этом случае
![]() ,
получаем уравнения прямой, которая
проходит через заданные точки:
,
получаем уравнения прямой, которая
проходит через заданные точки:
![]() .
.
Например,
уравнение прямой, которая проходит
через две заданные точки M1
(x1,
y1),
M2
(x2,
y2):
![]()
Общие уравнения прямой
Проанализируем систему из двух уравнений I степени:
![]() (3.4)
(3.4)
Каждое
из уравнений системы является определителем
плоскости в пространстве, а вся система,
при условии непараллельности плоскостей,
— прямую, по которой они пересекаются.
Эти уравнения именуют общими уравнениями
прямой. Направляющий вектор подобной
прямой определяется по формуле
![]() ,
где N1,
N2
– нормальные векторы плоскостей.
,
где N1,
N2
– нормальные векторы плоскостей.
Задача.
Даны общие уравнения прямой L:![]()
Вывести её канонические уравнения.
Определяем
направляющий вектор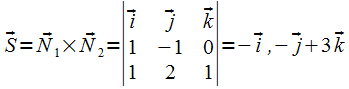 .
.
Для определения координат опорной т. L, имеем систему для определения x0, y0:

Следовательно,
канонические уравнения прямой L
имеют следующий вид:
![]()
