59. Базис, разложение вектора по базису, координаты вектора.

Базис образуют два линейно независимых вектора на плоскости (или три линейно независимых вектора в пространстве), если любой вектор плоскости (пространства) может быть представлен в виде их линейной комбинации.

Числовые коэффициенты этой линейной комбинации называются координатами данного вектора в рассматриваемом базисе:

если a, b, c – базис и d = ka + mb + pc, то числа k, m, p есть координаты вектора d в базисе a, b, c.

Свойства базиса:

- Любые два неколлинеарных вектора образуют базис на плоскости, а любые три некомпланарных вектора – базис в пространстве.

- Разложение данного вектора по данному базису единственно, т.е. его координаты в данном базисе определяются единственным образом.

- При сложении двух векторов их координаты относительно любого базиса складываются.

- При умножении вектора на число все его координаты умножаются на это число.

60. Изменение координат при сложении векторов и умножении вектора на число, координаты коллинеарных векторов.

Координаты данных векторов происходит по аксиомам Вейля:

(целые числа); λ для любого и для любого х (действительное число)

1) 2)

3) существует такой нулевой вектор , который прибавляя к вектору равен самому вектору : ;

4) для любого и существует (- ) такой что:

5) если 6)

7) 8)

61. Ортогональный и ортонормированный базис, направляющие косинусы.

Базис называется ортогональным, если он состоит из векторов лежащих на взаимно перпендикулярных прямых.

Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице.

Направляющие косинусы – это косинусы углов, образованных вектором и осями декартовой системы координат. (фактическая проекция вектора на необходимую ось).

Свойства направляющих косинусов:

1. X = |d| cosα, Y = |d| cosβ, Z = |d| cosγ.

2. , , .

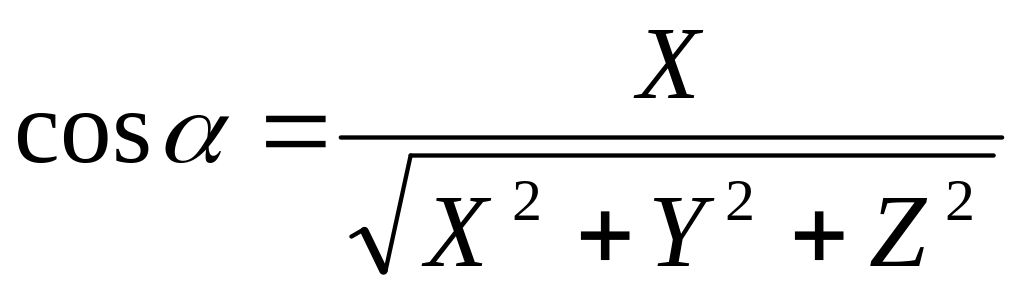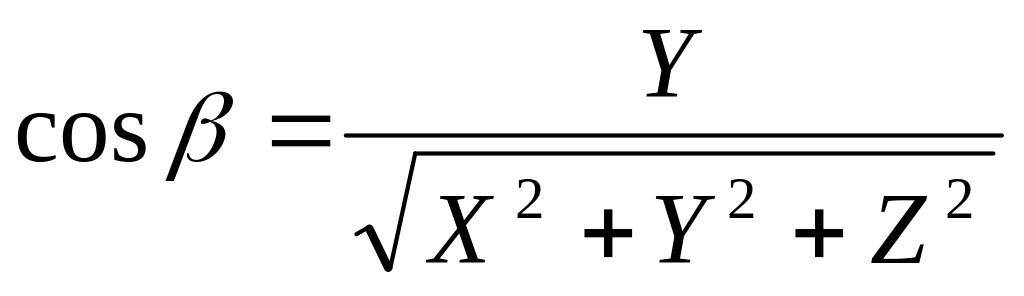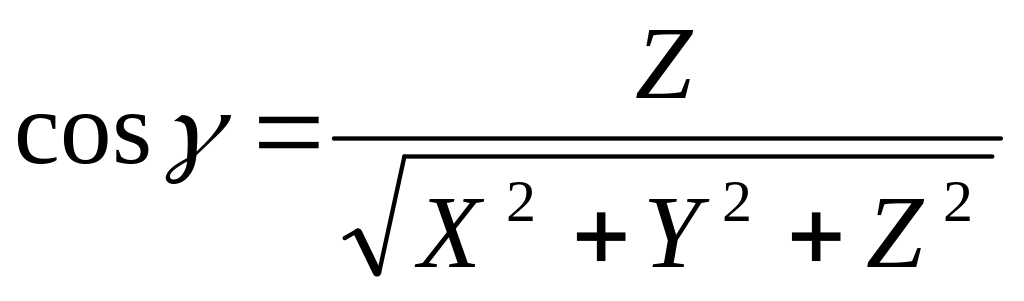3. cos²α + cos²β + cos²γ = 1.

62. Скалярное произведение векторов. Ортогональные вектора, скалярный квадрат.

Скалярным произведением векторов и называется число, равное произведению длин этих сторон на косинус угла между ними:  =   cos

Ортогональные вектора – вектора перпендикулярные друг другу. Скалярное произведение которых равно 0, т.к. cos90⁰=0

Скалярный квадрат – это скалярное произведение вектора самого на себя, и равно квадрату длинны данного вектора.

 =   cos0⁰ =  ² ≥ 0

63. Свойства скалярного произведения, вычисление скалярного произведения через координаты вектора.

Свойства скалярного произведения:

1.  =  ²;

2.  = 0, если  или = 0 или = 0.

3.  =  ;

4. ( + ) =  +  ;

5. (m ) = (m ) = m(  );

If рассм-ть векторы в декартовой прямоугольной системе координат, то  = x_a x_b + y_a y_b + z_a z_b;

64. Правая тройка векторов.

Тройка некомпланарных векторов abc называется правой (левой), если после приведения к общему началу вектор с располагается по ту сторону от плоскости, определяемой векторами а и b, откуда кратчайший поворот от а к b кажется совершающимся против часовой стрелки (по часовой стрелке).

с с

b a

a b

abc – правая тройка abc – левая тройка