16. Равномерное, показательное, нормальное распределения. Их функции распределения.

Опр. Говорят, что случайная величина Х равномерно распределена на отрезке [a, b], если она непрерывна и имеет плотность вероятности:

Найдем функцию распределения равномерно распределенной случайной величины X.

а) x≤a ;

б) a<x≤b .

в) x>b .

17. Лемма о нормальном распределении. Критерий независимости дискретной и непрерывной св.

Теорема 1. Если случайная величина Х имеет нормальное стандартное распределение с параметрами (a, ), то случайная величина имеет нормальное распределение, т.е. . ▲ ; .▲

Теорема 2. (Критерий независимости дискретных случайных величин).

Для того чтобы дискретные случайные величины Х₁,…,Х_n были независимы, необходимо и достаточно, чтобы для любых действительных чисел х₁,…,х_n выполнялось соотношение .

Теорема 3. (Критерий независимости для непрерывных случайных величин).

Для того чтобы непрерывные случайные величины Х₁, Х₂,…,Х_n были независимыми, необходимо и достаточно, чтобы для любых действительных чисел х₁,…,х_n выполнялось соотношение . Где совместимая плотность распределения случайных величин Х₁,…,Х_n, то есть совместимая функция распределения случайных величин Х₁,…,Х_n

.

18. Случайный вектор. Свойства функций распределения случайного вектора.

Опр. Вектор , где —случайные величины, называются n-мерным случайным вектором.

Т.о., случайный вектор отображает пространство элементарных исходов Ω→ в n-мерное действительное пространство .

Опр. Функция

называется функцией распределения случайного вектора или совместной функцией распределения случайных величин .

Свойства функции распределения случайного вектора:

1. .

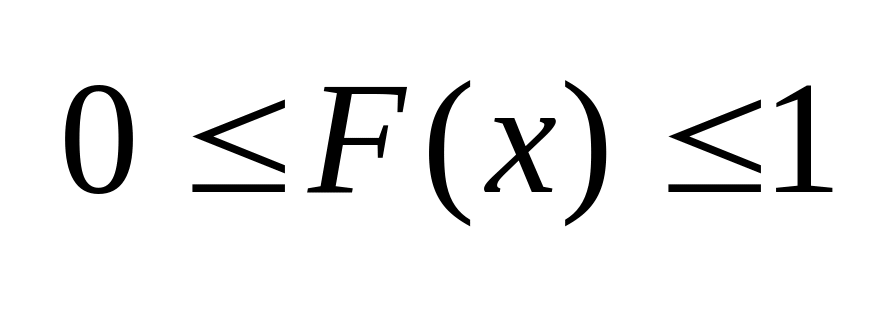2. Функция распределения случайного вектора неубывающая по каждому аргументу. ▲ Пусть x₁<y₁, тогда событие 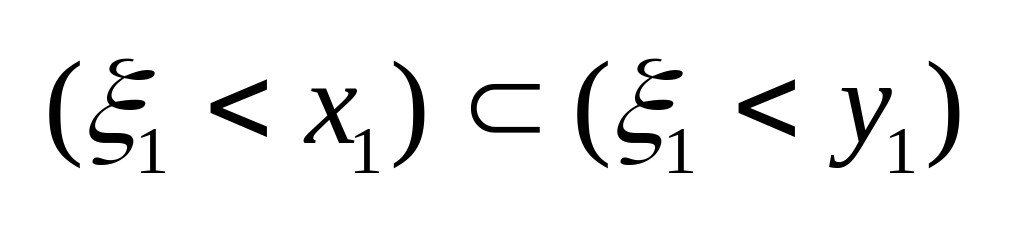. Тогда . По свойству вероятности если , то , получим . Т.е. функция не убывает по первому аргументу. Аналогично для любого аргумента. ▲

19. Случайный вектор. Свойства плотности распределения

Опр. Вектор , где —случайные величины, называются n-мерным случайным вектором.

Т.о., случайный вектор отображает пространство элементарных исходов Ω→ в n-мерное действительное пространство .

Опр. Функция

называется функцией распределения случайного вектора или совместной функцией распределения случайных величин .

Опр. Случайный вектор называется дискретным, если все его компоненты—дискретные случайные величины.

Опр. Случайный вектор называется непрерывным, если существует неотрицательная функция , называется плотностью распределения случайных величин такая, что функция распределения .

20. Функция двух случайных аргументов. Формула свертки.

Опр. Если каждой паре возможных значений случайных величин X и Y соответствует одно возможное значение случайной величины Z, то Z называют функцией двух случайных аргументов X и Y: .

Случай 1. Пусть Х и Y—дискретные независимые случайные величины. Для того чтобы составить закон распределения функции Z=X+Y, надо найти все возможные значения Z и их вероятности. Иными словами, составляется ряд распределения случайной величины Z.

Рассмотрим общий случай: Пусть Х и Y—независимые случайные величины, принимающие значения . Обозначим через , , . Z=X+Н. Обозначим через

. Таким образом, —формула свертки.