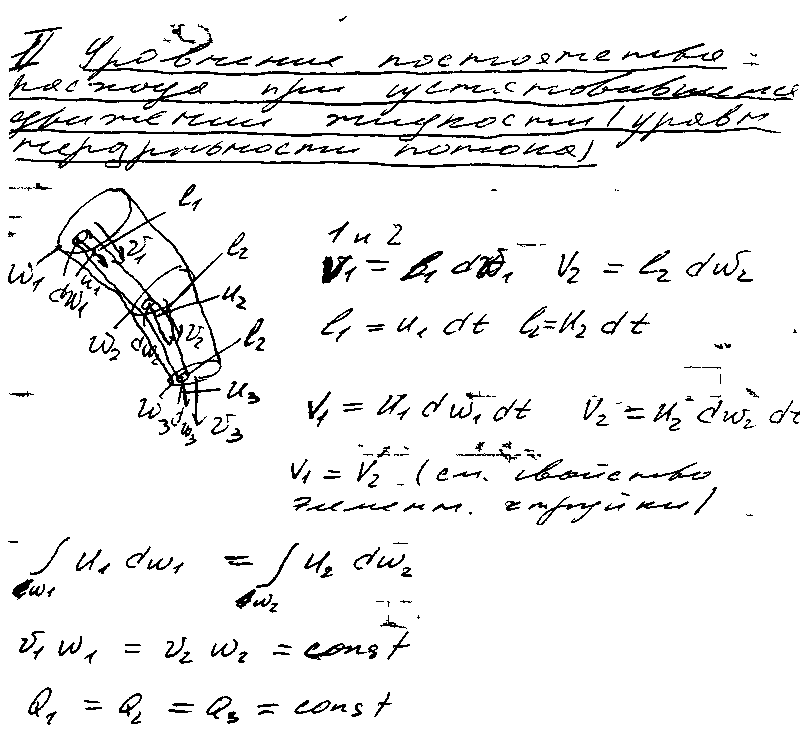- •1)Развитие гидравлики как наукиПрименение и значение гидравлики в современной технике, в лесной и деревообрабатывающей промышленности.
- •5) Гидростатическое давление и его свойства. Единицы измерения.
- •35) Закон Паскаля
- •26) Гидравлический удар в напорных трубопроводах и способы его предотвращения
- •6) Основное уравнение гидростатики. Дифференциальное уравнение равновесия жидкости
- •7)Пьезометрическая высота и пьезометрический напор. Их геометрический и физический смысл.
- •14) Виды движения жидкости
- •9) Приборы для измерения давления
- •12) Плавание тел. Закон Архимеда
- •10) Силы давления жидкости на плоские поверхности. Определение точки приложения.
- •11) Силы давления жидкости на криволинейные поверхности. Определение точки приложения.
- •13) Остойчивость плавающих тел, полностью или частично погруженных в жидкость
- •20) Два режима движения жидкости. Критерий рейнольдца
- •21) Гидравлический расчет простых длинных трубопроводов
- •27) Истечение жидкости через малое отверстие в тонкой стенке при постоянном напоре
- •28 ) Истечение жидкости через насадКи. Типы насадков и их применение в технике.
- •29) Истечение жидкости при переменном напоре. Опорожнение сосудов
- •31) Центробежные насосы. Устройство и принцип действия
- •30) Характеристика центробежных насосов.
- •19) Равномерное движение жидкости в открытых руслах
- •18) Общие сведения о гидравлических потерях. Виды гидравлических потерь. Гидравлический уклон.
- •2 3) Местные гидравлические сопротивления
- •17) Уравнение бернулли для потока реальной жидкости Графическое изображение членов уравнения
- •24) Расчет гидравлически коротких трубопроводов. Особенности расчёта сифонов
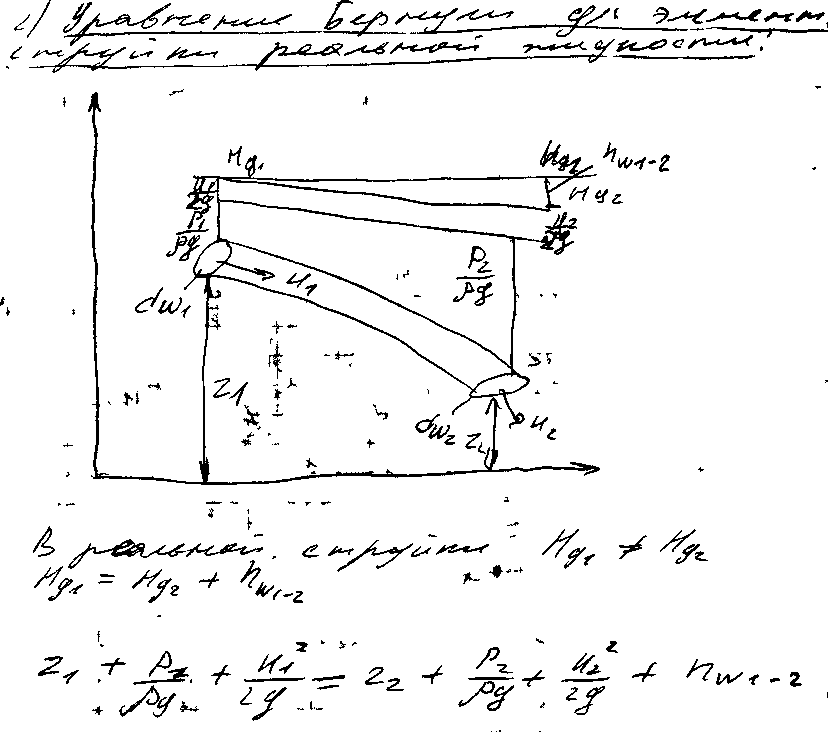
17) Уравнение бернулли для потока реальной жидкости Графическое изображение членов уравнения
Произведем вывод уравнения Бернулли для потока реальной жидкости (рис. 31, в), которое главным образом и применяется в расчетной практике. Имеем уравнение Бернулли для элементарной струйки для реальной жидкости:
Д![]() ля
получения уравнения Бернулли для целого
потока необходимо просуммировать
энергию всех элементарных струек потока
и потери энергии, образовавшиеся при
его движении. Чтобы найти энергию всех
элементарных струек потока, умножим
все члены, входящие в уравнение , на
pgdQ,
тогда,
интегрируя, будем иметь
ля
получения уравнения Бернулли для целого
потока необходимо просуммировать
энергию всех элементарных струек потока
и потери энергии, образовавшиеся при
его движении. Чтобы найти энергию всех
элементарных струек потока, умножим
все члены, входящие в уравнение , на
pgdQ,
тогда,
интегрируя, будем иметь
![]()
24) Расчет гидравлически коротких трубопроводов. Особенности расчёта сифонов
Во многих случаях местные потери напора, величиной которых мы пренебрегали при расчете гидравлически длинных трубопроводов, достигают величин, сопоставимых с потерями напора по длине. В этом случае пренебрегать ими не следует, так как это может привести к грубым ошибкам. К таким случаям относятся, например, системы гидропривода, сифоны, всасывающие трубы насосов и т. д. При этом, так как часто мы имеем дело с жидкостью, вязкость которой может намного превосходить вязкость воды, в общем случае при определении потерь напора по длине пользуются не формулой (252), а более общей формулой Дарси (219) и коэффициент гидравлических сопротивлений трения К определяют в зависимости от области движения по одной из зависимостей, указанных в § 31, гл. VI.
В качестве примера расчета рассмотрим гидравлически короткие трубопроводы, представленные на рис 51. Первый случай — истечение жидкости под уровень. Пусть жидкость из верхнего резервуара А (рис. 51, а) по трубопроводу перетекает в нижний резервуар В. Длина трубопровода равна /, его внутренний диаметр d; разность отметок уровня жидкости в верхнем и нижнем резервуарах равна Н, кроме того, что отметки уровней жидкости поддерживаются постоянными, движение жидкости установившееся. Для определения расхода жидкости воспользуемся уравнением Бернулли, которое напишем для сечений, где имеется мак-с пмум известных величин. В качестве таких сечений примем сечения /—/ и 2—2, а за плоскость сравнения — плоскость 0—0. Нетрудно видеть, что в этом случае, пренебрегая скоростными майорами в сечениях /—/ и 2—2 и полагая, что в этих сечениях давление равно атмосферному, уравнение Бернулли можно записать так:
|![]() дс
hw
—
общие потери напора от сечения /—/ до
сечения 2—2.
Потери
напора hw
слагаются
из потерь напора по длине мссшых потерь
напора. В соответствии со схемой
трубопровода Mtx'iiiue
потери состоят из потерь напора на вход
в трубу, потерь напора в кране, потерь
напора на два поворота, потерь напора
в кране и, наконец, потерь напора на
выход из трубы в нижний резервуар В.
Если
все эти местные сопротивления
располагаются на достаточном
расстоянии (не оказывают поэтому
взаимного влияния друг на друга), то
общие потери напора будут равны
алгебраической сумме местных потерь
напора Л/ и потерьнапора по длине ft,-
дс
hw
—
общие потери напора от сечения /—/ до
сечения 2—2.
Потери
напора hw
слагаются
из потерь напора по длине мссшых потерь
напора. В соответствии со схемой
трубопровода Mtx'iiiue
потери состоят из потерь напора на вход
в трубу, потерь напора в кране, потерь
напора на два поворота, потерь напора
в кране и, наконец, потерь напора на
выход из трубы в нижний резервуар В.
Если
все эти местные сопротивления
располагаются на достаточном
расстоянии (не оказывают поэтому
взаимного влияния друг на друга), то
общие потери напора будут равны
алгебраической сумме местных потерь
напора Л/ и потерьнапора по длине ft,-
В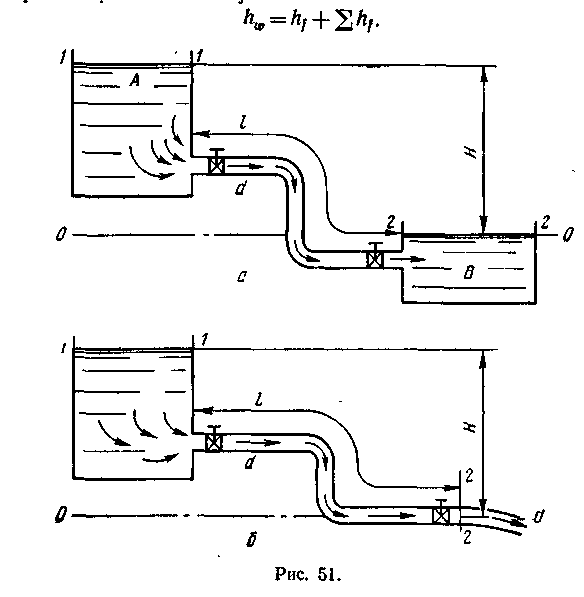 рассматриваемом случае
рассматриваемом случае
г![]() де
слагаемые в правой части соответственно
выражают местные потери напора на
вход (/1Вх),
в кране (Лк),
на поворот {Л„) и на выход (/гВЫх).
де
слагаемые в правой части соответственно
выражают местные потери напора на
вход (/1Вх),
в кране (Лк),
на поворот {Л„) и на выход (/гВЫх).
Каждую из этих потерь напора можно выразить через скоростные напоры, воспользовавшись формулой Вейсбаха. Например, потери на вход
в кране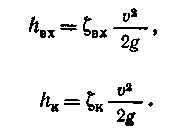
 Расчет
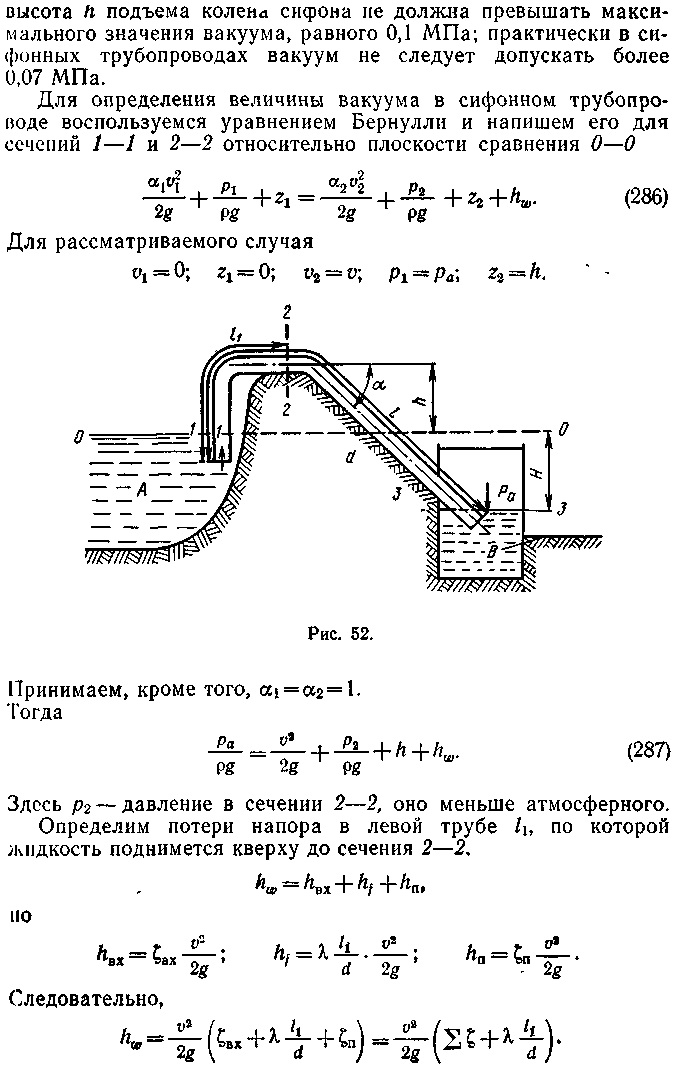
сифонного трубопровода.
Сифоном или сифонным трубопроводом
называют такой трубопровод, часть
которого располагается выше уровня
жидкости верхнего резервуара (рис. 52).
Расчет
сифонного трубопровода.
Сифоном или сифонным трубопроводом
называют такой трубопровод, часть
которого располагается выше уровня
жидкости верхнего резервуара (рис. 52).
 Сифонные
трубопроводы часто применяют в практике
в связи с тем, что они являются более
экономичными, чем, например, самотечный
трубопровод, движение жидкости в котором
обусловлено разностью уровней. При
устройстве самотечного трубопровода
нужно иногда выполнить большой объем
земляных работ. При прокладывании
сифонного трубопровода земляные работы
выполняются в небольшом объеме, так как
трубу укладывают по поверхности земли
или на малой глубине. Недостатком
сифонного трубопровода является то,
что он начинает работать только после
заливки его жидкостью. Кроме того, в
связи с накоплением газов в колене
сифона он начинает работать неполным
сечением и может прекратить свою работу,
если не принять необходимых мер. Для
устранения этого явления в колене
сифона при помощи вакуум-насоса
производится отсос воздуха. Течение
жидкости по сифонному трубопроводу
происходит благодаря разности между
внешним давлением ра
и
давлением внутри сифона, а также напору,
созданному разностью уровней жидкости
в двух резервуарах А
и
В.
Сифонные
трубопроводы часто применяют в практике
в связи с тем, что они являются более
экономичными, чем, например, самотечный
трубопровод, движение жидкости в котором
обусловлено разностью уровней. При
устройстве самотечного трубопровода
нужно иногда выполнить большой объем
земляных работ. При прокладывании
сифонного трубопровода земляные работы
выполняются в небольшом объеме, так как
трубу укладывают по поверхности земли
или на малой глубине. Недостатком
сифонного трубопровода является то,
что он начинает работать только после
заливки его жидкостью. Кроме того, в
связи с накоплением газов в колене
сифона он начинает работать неполным
сечением и может прекратить свою работу,
если не принять необходимых мер. Для
устранения этого явления в колене
сифона при помощи вакуум-насоса
производится отсос воздуха. Течение
жидкости по сифонному трубопроводу
происходит благодаря разности между
внешним давлением ра
и
давлением внутри сифона, а также напору,
созданному разностью уровней жидкости
в двух резервуарах А
и
В.

 При
расчете сифонного трубопровода обычно
требуется определить максимальную
величину вакуума в сифоне, а также
диаметр трубы при заданном расходе Q
или величину вакуума и расход при
заданном диаметре трубопровода. Заметим,
что
При
расчете сифонного трубопровода обычно
требуется определить максимальную
величину вакуума в сифоне, а также
диаметр трубы при заданном расходе Q
или величину вакуума и расход при
заданном диаметре трубопровода. Заметим,
что

16) Уравнение Бернулли для элементарной струйки идеальной и реальной жидкости. Толкование уравнения Бернулли
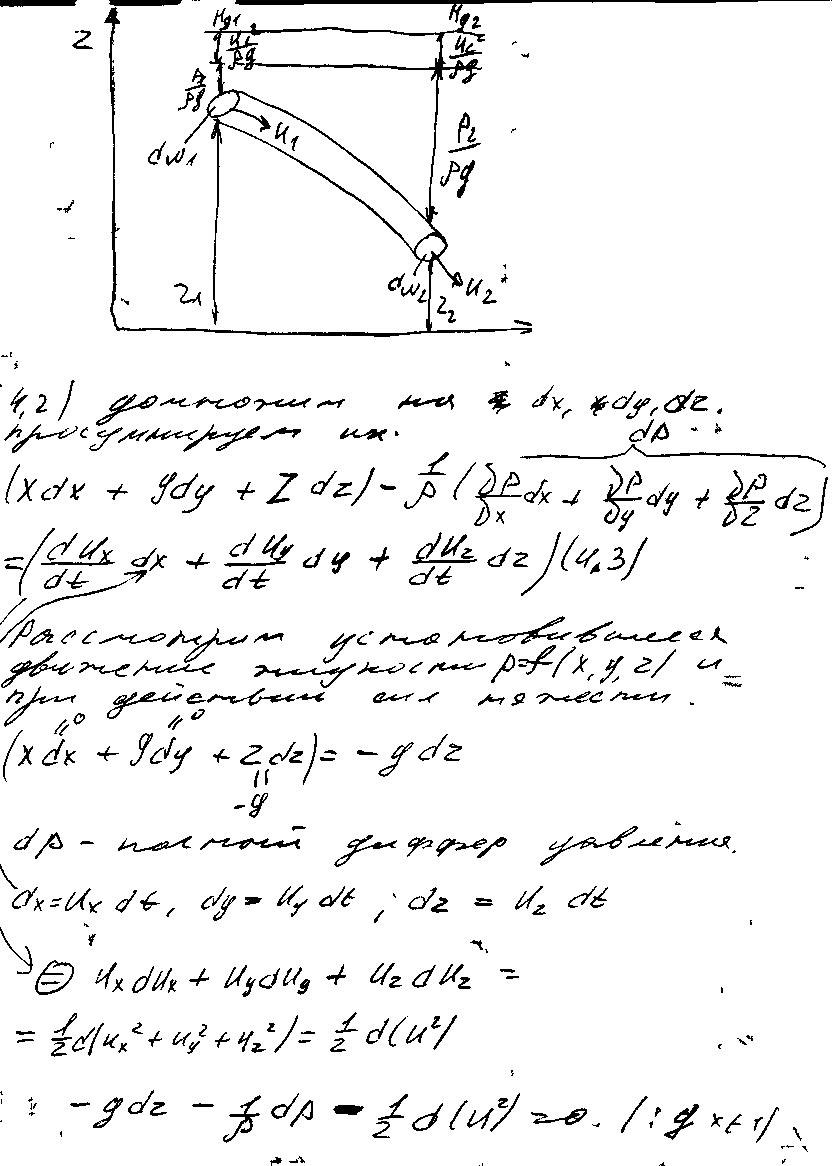
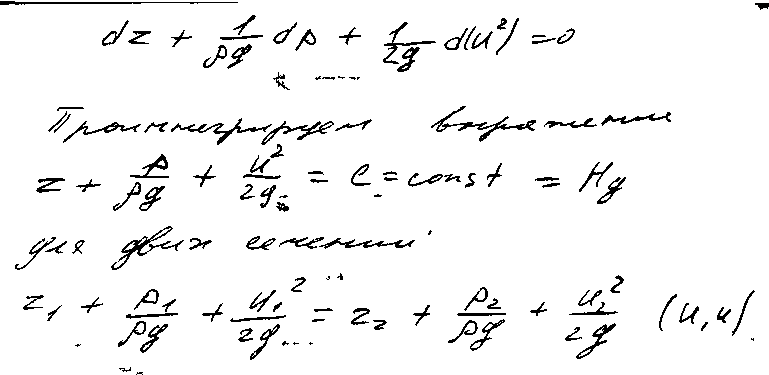
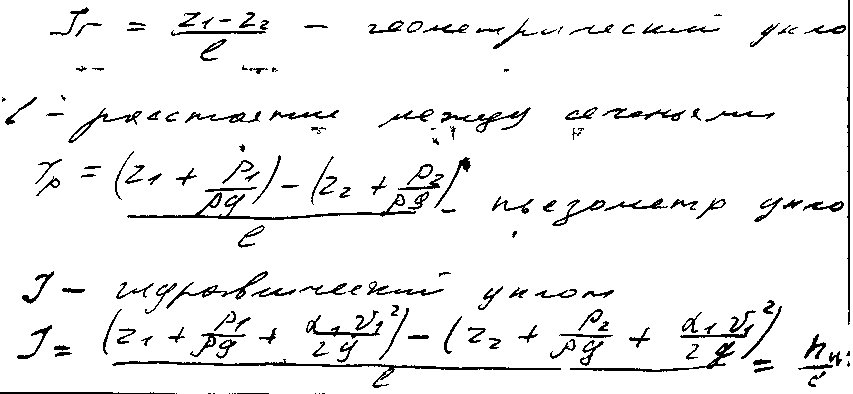
22) Турбулентное движение жидкости.
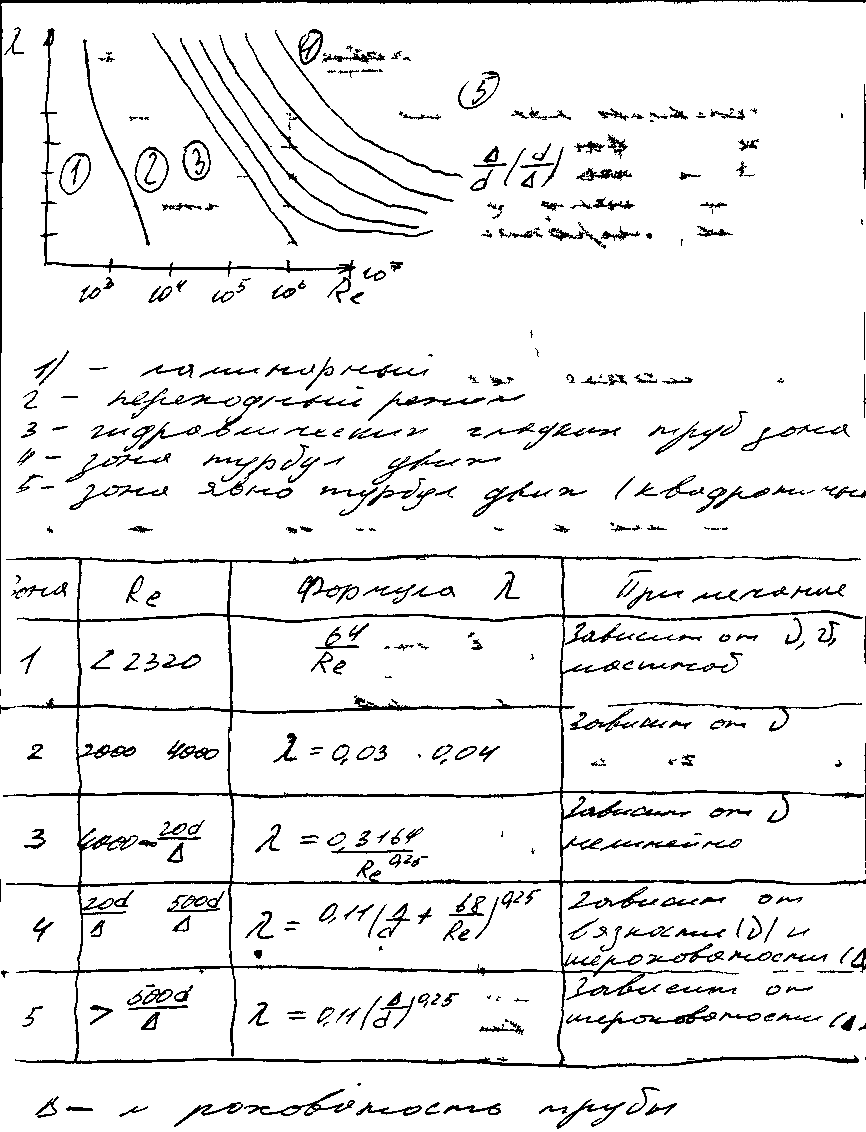
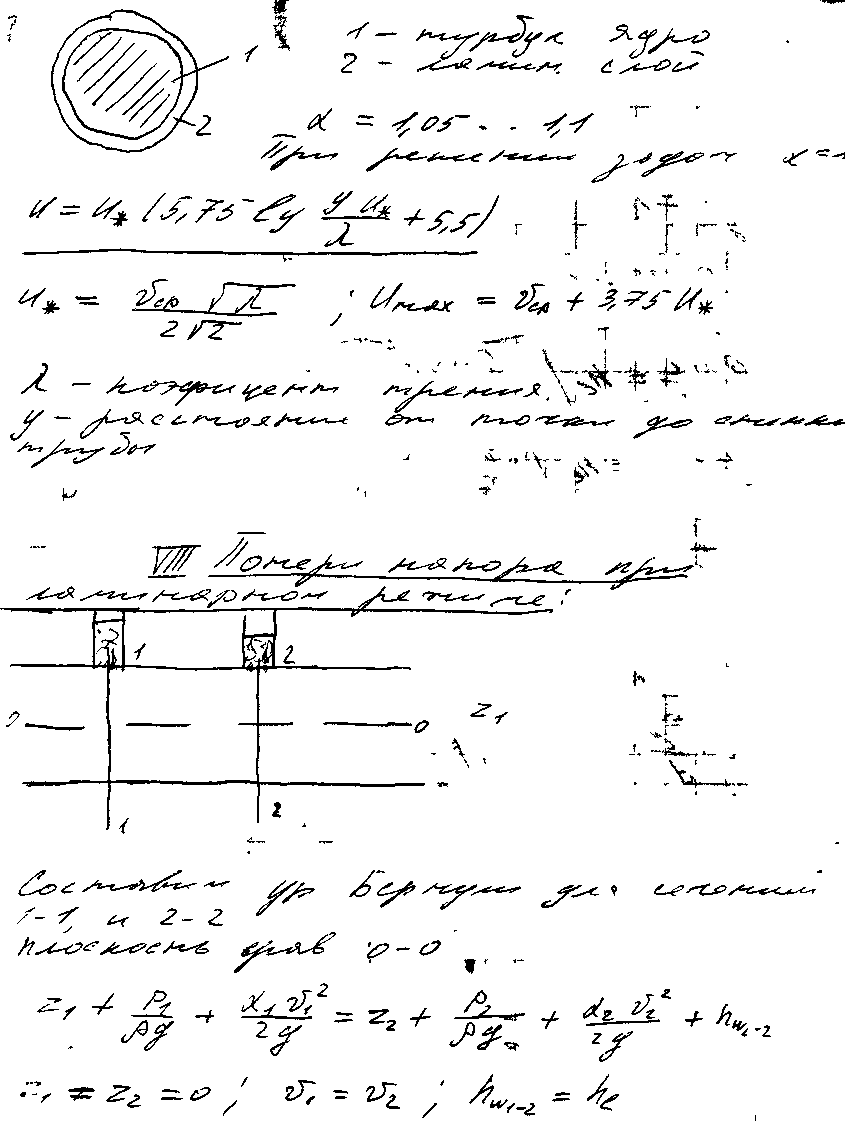 Потери
напора, понятие о шероховатости стенок.
Потери
напора, понятие о шероховатости стенок.

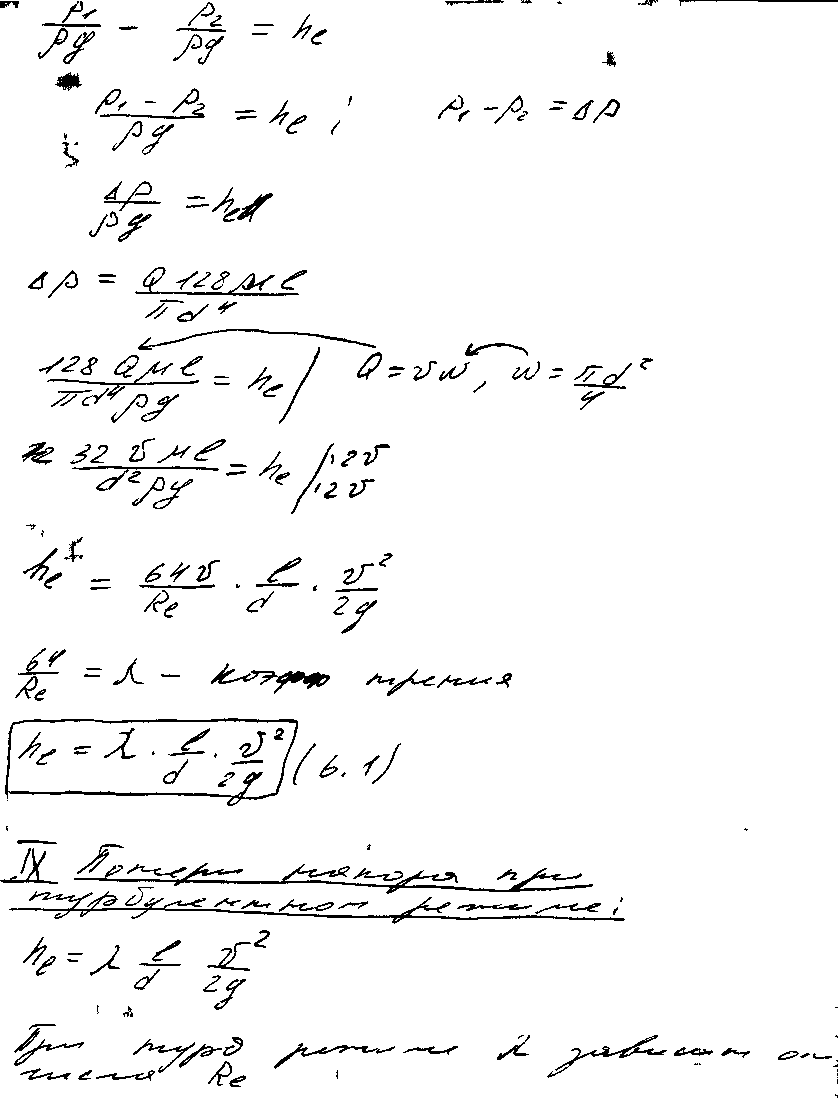

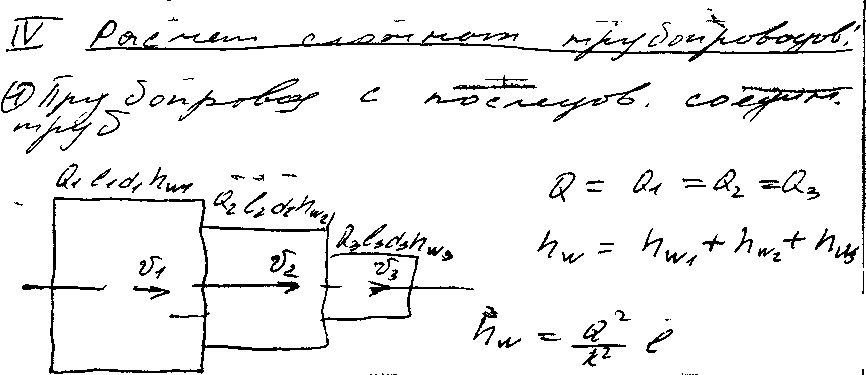
25) Параллельное и последовательное соединение трубопроводов и их гидравлический расчет
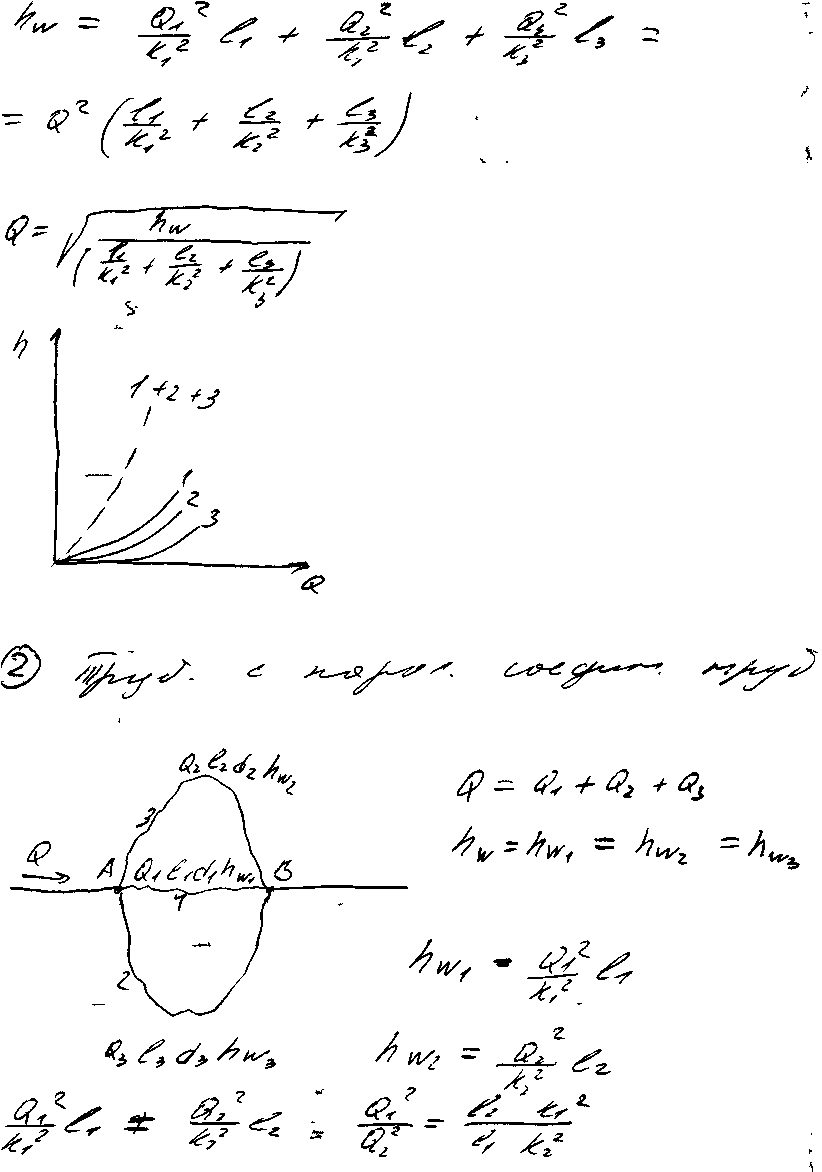
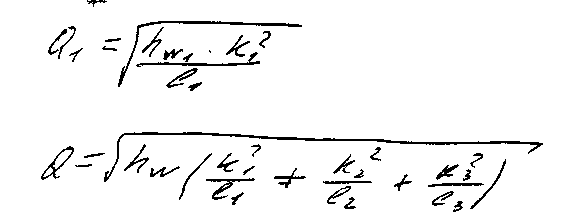
15) Поток жидкости. Основные элементы потока.
Уравнение неразрывности.