Закон сохранения механической энергии

В системе тел, между которыми действуют только консерватив­ные силы, полная механическая энергия сохраняется, т. е. не из­меняется со временем.

Закон сохранения энергии — следствие однородности времени

Однородность времени проявляется в том, что физические законы ин­вариантны относительно выбора начала отсчета времени. Например, при свободном падении тела в поле сил тяжести его скорость и пройденный путь зависят лишь от начальной скорости и продолжительности свобод­ного падения тела и не зависят от того, когда тело начало падать.

1.42 Консервативные системы и закон сохранения энергии_ Консервативные системы

Механические системы, на тела которых действуют только консерватив­ные силы (внутренние и внешние).

Еще формулировка закона сохранения энергии_

В консервативных системах полная механическая энергия сохраняется, т. е. не изменяется с течением времени.

Превращение энергии на примере свободного падения тела (сопротивление не учитывается)_________________________________________________________________

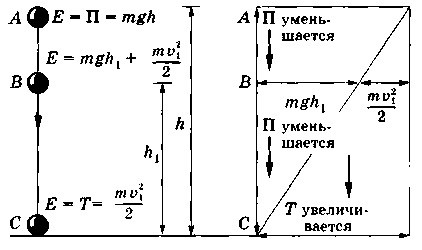
В консервативных систе­мах полная механическая энергия сохраняется, т.е. Е = const. Могут происхо­дить лишь превращения ки­нетической энергии в потен­циальную и обратно в экви­валентных количествах так, что полная энергия остается неизменной (что и проде­монстрировано на рисунке).

1.43 Закон сохранения и превращения энергии_____________________________________

Диссипативная система_________________________________________________________________________

Система, в которой механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические) формы энергии. Этот процесс получил название диссипации (или рассеяния) энергии.

Об энергии в случае неконсервативных систем____________________________________________________

Все системы в природе, строго говоря, являются диссипативными. В сис­теме, в которой действуют также неконсервативные силы, например силы трения, полная механическая энергия системы не сохраняется. Следовательно, в этих случаях закон сохранения механической энергии несправедлив. Однако при «исчезновении» механической энергии всегда возникает эквивалентное количество энергии другого вида.

Закон сохранения и превращения энергии___________________________________________________________

Энергия никогда не исчезает и не появляется вновь, она лишь превраща­ется из одного вида в другой.

В этом и заключается физическая сущность закона сохранения и превра­щения энергии — сущность неуничтожимости материи и ее движения.

Этот закон — фундаментальный закон природы, он справедлив как для систем макроскопических тел, так и для систем микротел.

1.3.4. Графическое представление энергии

1.44 Потенциальные кривые и их анализ на некоторых примерах____________________

Исходные данные_______________________________________________________________________________

• Рассматривается одномерное движение тела (потенциальная энергия — функция лишь одной переменной).

• Рассматриваются только консервативные системы (в них механиче­ская энергия превращается только в механическую).

Потенциальная кривая___________________________________________________________________________

График зависимости потенциальной энергии от некоторого аргумента.

Анализ потенциальной кривой для тела в однородном поле тяжести_____________________________________

П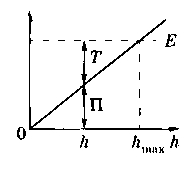 отенциальная кривая П(Н) = П = mgh — прямая линия, проходящая через начало координат, угол наклона которой к оси h тем больше, чем больше масса т тела (tg α = mg). График заданной полной энергии тела Е — прямая ЕЕ, параллельная оси h.

• Потенциальная энергия П тела на высоте h опре­деляется отрезком вертикали, заключенным между точкой h на оси абсцисс и потенциальной кривой.

• Кинетическая энергия Т тела на высоте h задается ординатой между потенциальной кривой и горизонтальной прямой ЕЕ.

• Если h = h_шах, то T = 0 иП=E = mgh_max, т. е. потенциальная энергия становится максимальной и равной полной энергии.

• Скорость тела на высоте h: