
- •1) Перестановка
- •2 ) Определитель
- •4) Миноры алгебраические дополнения
- •6) Проекция вектора на ось это число или скаляр.
- •8) Векторное произведение векторов
- •9) Смешанное произведение векторов
- •10) Линия на плоскости
- •11) Кривые второго порядка
- •12) Поверхность в пространстве
- •- Уравнение плоскости, проходящей через три точки.
- •13) Линия в пространстве
- •14) Комплексные числа
- •15) Возведение в целую степень и извлечение корня из комплексного числа
- •16) Многочлен. Сложение, умножение и деление многочлена.(?) Теорема Безу
- •17) Корень многочлена
- •19. Многочлены с действительными коэффициентами. Теоремы о многочленах с действительными коэффициентами
- •20. Понятие матрицы. Диагональные и треугольные матрицы. Транспонирование матриц. Сложение(вычитание) матриц, умножение матрицы на число. Свойства сложения матриц. Свойство умножения матрицы на число
- •21. Умножение матриц. Свойства умножения матриц
- •22. Обратная матрица и её основные свойства. Критерий обратной матрицы
- •24. Понятие линейного пространства. Примеры линейных пространств
- •25. Понятие линейной зависимости (независимости) системы векторов. Основные свойства линейно зависимых и линейно независимых систем векторов. Критерий линейной зависимости системы векторов
- •26) . Понятие линейной зависимости(независимости) системы векторов. Геометрический смысл линейной зависимости и независимости для системы геометрических векторов
- •27)Что называют системой образующих линейного пространства? Дайте два определения базиса в лин. Пространстве. Каким из этих определений удобнее пользоваться при решении задач?
- •28)Размерность и базис линейного пространства. Теорема о разложении векторов по базису
- •29)Преобразование координат вектора при переходе к другому базису. Матрица перехода от одного базиса к другому
- •30)Что называют линейным подпространством в линейном пространстве?
26) . Понятие линейной зависимости(независимости) системы векторов. Геометрический смысл линейной зависимости и независимости для системы геометрических векторов
Вектор , называется линейной комбинацией векторов . Набор чисел называется не тривиальным, если хотя бы одно из этих чисел не равно нулю. Если все числа равны нулю, то такой набор называется тривиальным.
По определению, система векторов линейного пространства называется линейно зависимой, если существует нетривиальный набор чисел , для которого . Если же только при тривиальном наборе чисел (т.е. для любого нетривиального набора ), то система называется линейно независимой.
Геометрический смысл
Векторы
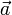 и
и 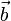 линейно
зависимы тогда и только тогда, когда
они коллинеарные (лежат
на параллельных
прямых).
линейно
зависимы тогда и только тогда, когда
они коллинеарные (лежат
на параллельных
прямых).Векторы
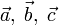 линейно
зависимы тогда и только тогда, когда
они компланарны (лежат
в одной плоскости).
линейно
зависимы тогда и только тогда, когда
они компланарны (лежат
в одной плоскости).
27)Что называют системой образующих линейного пространства? Дайте два определения базиса в лин. Пространстве. Каким из этих определений удобнее пользоваться при решении задач?
Линейно
независимая система
![]() линейного пространства
называется максимальной линейно
независимой системой, если
линейного пространства
называется максимальной линейно
независимой системой, если
![]() расширенная система
расширенная система
Определение Базисов:
1) Базисом линейного пространства является любая максимальная линейно независимая система
2) Второе определение базиса линейного пространства : базисом называется полная, линейно независимая система векторов.
Удобнее второе определение.
28)Размерность и базис линейного пространства. Теорема о разложении векторов по базису
1) Базисом линейного пространства является любая максимальная линейно независимая система
2) Второе определение базиса линейного пространства : базисом называется полная, линейно независимая система векторов.
Размерность:
Все базисы линейного пространства содержат одинаковое число векторов. Это число называется размерностью линейного пространства.
Теорема
Любой
вектор
![]() можно разложить по базису
можно разложить по базису
![]() ,
т.е. представить вектор
в виде линейной комбинации
,
т.е. представить вектор
в виде линейной комбинации
![]() .
(2)
.
(2)
Причем разложение вектора единственно (не существует двух или более различных разложений вектора по базису).
Набор
чисел
![]() в разложении (2) называется координатами
вектора
в базисе
.
в разложении (2) называется координатами
вектора
в базисе
.
29)Преобразование координат вектора при переходе к другому базису. Матрица перехода от одного базиса к другому
Набор чисел в разложении (2) называется координатами вектора в базисе .
Матрицей
перехода от базиса ![]() к базису
к базису ![]() является матрица,
столбцы которой — координаты
разложения векторов
в
базисе
.
является матрица,
столбцы которой — координаты
разложения векторов
в
базисе
.
Если ее определитель отличен от
нуля то матрица невырождена и у нее существует обратная матрица
30)Что называют линейным подпространством в линейном пространстве?
По
определению, множество
![]() ,
вложенное в линейное пространство
и само являющееся линейным пространством,
называется линейным подпространством
пространства
,
вложенное в линейное пространство
и само являющееся линейным пространством,
называется линейным подпространством
пространства
Линейная оболочка системы векторов.
. Линейной оболочкой системы векторов
называется
множество
![]() всех
векторов
,
где
всех
векторов
,
где
. Любая линейная оболочка, построенная в линейном пространстве , является линейным подпространством пространства , либо совпадает с самим пространством
