Линейная алгебра N 12
.doc
Занятие 12. Комплексные числа.
12.1. Определение комплексных чисел в алгебраической форме. Сравнение и изображение комплексных чисел на комплексной плоскости. Комплексное сопряжение. Сложение, умножение, деление комплексных чисел.
12.2. Модуль, аргумент комплексного числа.
12.3. Тригонометрическая и показательная формы записи комплексного числа.
12.4. Возведение в целую степень и извлечение корня из комплексного числа.
Определение комплексных чисел в алгебраической форме. Сравнение и изображение комплексных чисел на комплексной плоскости. Комплексное сопряжение. Сложение, умножение, деление комплексных чисел.
Комплексным числом в алгебраической форме называется число
,
(1)
где
называется мнимой единицей и
- действительные числа:
называется действительной (вещественной)
частью;
- мнимой частью комплексного числа
.
Комплексные числа вида
называются чисто мнимыми числами.
Множество всех комплексных чисел
обозначается буквой
.
По определению,
,
и т.д.
Множество всех действительных чисел
является частью множества
:
.
С другой стороны, существуют комплексные
числа, не принадлежащие множеству
.
Например,
и
,
т.к.
.
Комплексные числа в алгебраической форме естественным образом возникают при решении квадратных уравнений с отрицательным дискриминантом.
Пример 1. Решить уравнение
.
Решение.
,
т.к.
.
Следовательно, заданное квадратное уравнение имеет комплексные корни
,
.
Пример 2. Найти действительную и мнимую части комплексных чисел
,
,
.
Решение.
- соответственно вещественная и мнимая
части числа
,
.
.
.
Любое комплексное число
изображается вектором на комплексной
плоскости
,
представляющей плоскость с декартовой
системой координат
.
Начало вектора лежит в точке
,
а конец - в точке с координатами
(рис
1.) Ось
называется
вещественной осью, а ось
- мнимой осью комплексной плоскости
.
Рис. 1.
Комплексные числа
сравниваются между собой только знаками
.
.
Если же хотя бы одно из равенств:
нарушено, то
.
Записи типа
не имеют смысла.
По определению, комплексное число
называется комплексно сопряженным
числу
.
В этом случае пишут
.
Очевидно, что
.
Везде далее черта сверху над комплексным
числом будет означать комплексное
сопряжение.
Например,
.
Над комплексными числами можно выполнять такие операции, как сложение (вычитание), умножение, деление.
1. Сложение комплексных чисел
производится так:
.
Свойства операции сложения:
- свойство коммутативности;
- свойство ассоциативности.
Нетрудно видеть, что геометрически
сложение комплексных чисел
означает сложение отвечающих им на
плоскости
векторов по правилу параллелограмма.
Операция вычитание числа
из числа
производится так:
.
2. Умножение комплексных чисел
производится так:
.
Свойства операции умножения:
- свойство коммутативности;
- свойство ассоциативности;
- закон дистрибутивности.
3. Деление комплексных чисел
выполнимо только при
и производится так:
.
Пример 3. Найти
,
если
.
Решение.
1)
.(ош!)
2)
.(ош!)
3)
.(ош!)
4)
.
5)
.
Пример 4. Вычислить
,
если
.
Решение.
.
z, т.к.
.
.(ош!)
Нетрудно проверить (предлагается это
сделать самостоятельно) справедливость
следующих утверждений:
.
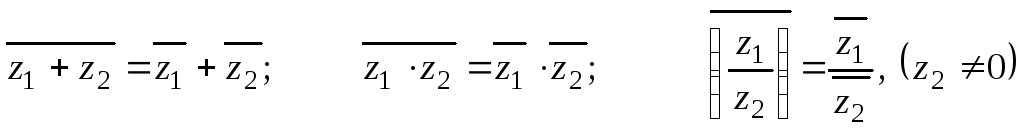Модуль, аргумент комплексного числа.
Модуль комплексного числа
(модуль
обозначается
)
это - неотрицательное число
,
т.е.
.
Геометрический смысл
- длина вектора, представляющего число
на комплексной плоскости
.
Уравнение
определяет множество всех чисел
(векторов на
),
концы которых лежат на единичной
окружности
.
Аргумент комплексного числа
(аргумент
обозначается
)
это – угол
в радианах между вещественной осью
и числом
на комплексной плоскости
,
причем
положителен, если он отсчитывается от
до
против часовой стрелки, и
отрицателен, если
отсчитывается от оси
до
по часовой стрелке.
Таким образом, аргумент числа
определяется неоднозначно, с точностью
до слагаемого
,
где
.
Однозначно аргумент числа
определяется в пределах одного обхода
единичной окружности
на плоскости
.
Обычно требуется найти
в пределах интервала
,
такое значение называется главным
значением аргумента числа
и обозначается
.
и
числа
можно найти из уравнения
,
при этом обязательно нужно
учитывать, в какой четверти плоскости
лежит конец вектора
- точка
:
если
(1-я четверть плоскости
),
то
;
если
(2-я четверть плоскости
),
то
;
если
(3-я четверть плоскости
),
то
;
если
(4-я четверть плоскости
),
то
.
Фактически, модуль и аргумент числа
,
это полярные координаты
точки
- конца вектора
на плоскости
.
Пример 5. Найти модуль и главное значение аргумента чисел:
.
Решение.
1)
.
2)
.
3)
.
4)
.
5)
.
6)
.
7)
.
8)
.
Аргументы чисел
,
лежащих осях
,
разделяющих четверти 1,2,3,4 комплексной
плоскости
,
находятся сразу же по графическим
изображениям этих чисел на плоскости
.
Тригонометрическая и показательная формы записи комплексного числа. Умножение и деление комплексных чисел в тригонометрической и показательной формах записи.
Тригонометрическая форма записи
комплексного числа
имеет вид:
,
(2)
где
-
модуль,
-
аргумент комплексного числа
.
Такое представление комплексных чисел
вытекает из равенств
.
Показательная (экспоненциальная)
форма записи комплексного числа
имеет вид:
,
(3)
где
-
модуль,
-
аргумент числа
.
Возможность представления комплексных
чисел в показательной форме (3) вытекает
из тригонометрической формы (2) и формулы
Эйлера:
.
(4)
Эта формула доказывается в курсе ТФКП (Теория функций комплексного переменного).
Пример 6. Найти тригонометрическую
и экспоненциальную формы записи
комплексных чисел:
из примера 5.
Решение. Воспользуемся результатами примера 5, в котором найдены модули и аргументы всех указанных чисел.
1)
- тригонометрическая форма записи числа
,
- показательная (экспоненциальная)
форма записи числа
.
2)
- тригонометрическая форма записи числа
,
- показательная (экспоненциальная)
форма записи числа
.
3)
- тригонометрическая форма записи числа
,
- показательная (экспоненциальная)
форма записи числа
.
4)
- тригонометрическая форма записи числа
,
- показательная (экспоненциальная)
форма записи числа
.
5)
- тригонометрическая форма записи числа
,
- показательная (экспоненциальная)
форма записи числа
.
6)
- тригонометрическая форма числа
,
- показательная (экспоненциальная)
форма числа
.
7)
- тригонометрическая форма записи числа
,
- показательная (экспоненциальная)
форма числа
.
8)
- тригонометрическая форма записи числа
,
- показательная (экспоненциальная)
форма записи числа
.
Показательная форма записи комплексных
чисел приводит к следующей геометрической
трактовке операций умножения и деления
комплексных чисел. Пусть
- показательные формы чисел
.
1.
При перемножении комплексных чисел
их модули перемножаются, а аргументы
складываются.
2.
При делении комплексного числа
на число
получается комплексное число
,
модуль
которого равен отношению модулей
,
а аргумент
- разности
аргументов чисел
.
Возведение в целую степень и извлечение корня из комплексного числа.
По определению,
.
При возведении в целую степень
комплексного
числа
,
следует действовать так: сначала найти
модуль
и аргумент
этого числа; представить
в показательной форме
;
найти
,
выполнив следующую последовательность
действий
,
где
.
(5)
Замечание. Аргумент
числа
может не принадлежать интервалу
.
В этом случае следует по полученному
значению
найти главное значение
аргумента
числа
,
прибавляя (или вычитая) число
с таким значением
,
чтобы
принадлежало интервалу
.
После этого, нужно заменить в формулах
(5)
на
.
Пример 7. Найти
и
,
если
.
Решение.
1)
=
(см. число
из примера 6).
2)
,
где
.
.
.
Следовательно,
можно заменить на
и, значит,
,
где
.
3)
,
где
.
.
Заменим
на
.
Следовательно,
.
Извлечение корня
-й
степени
из комплексного числа
проводится по формуле Муавра-Лапласа