
- •1) Перестановка
- •2 ) Определитель
- •4) Миноры алгебраические дополнения
- •6) Проекция вектора на ось это число или скаляр.
- •8) Векторное произведение векторов
- •9) Смешанное произведение векторов
- •10) Линия на плоскости
- •11) Кривые второго порядка
- •12) Поверхность в пространстве
- •- Уравнение плоскости, проходящей через три точки.
- •13) Линия в пространстве
- •14) Комплексные числа
- •15) Возведение в целую степень и извлечение корня из комплексного числа
- •16) Многочлен. Сложение, умножение и деление многочлена.(?) Теорема Безу
- •17) Корень многочлена
- •19. Многочлены с действительными коэффициентами. Теоремы о многочленах с действительными коэффициентами
- •20. Понятие матрицы. Диагональные и треугольные матрицы. Транспонирование матриц. Сложение(вычитание) матриц, умножение матрицы на число. Свойства сложения матриц. Свойство умножения матрицы на число
- •21. Умножение матриц. Свойства умножения матриц
- •22. Обратная матрица и её основные свойства. Критерий обратной матрицы
- •24. Понятие линейного пространства. Примеры линейных пространств
- •25. Понятие линейной зависимости (независимости) системы векторов. Основные свойства линейно зависимых и линейно независимых систем векторов. Критерий линейной зависимости системы векторов
- •26) . Понятие линейной зависимости(независимости) системы векторов. Геометрический смысл линейной зависимости и независимости для системы геометрических векторов
- •27)Что называют системой образующих линейного пространства? Дайте два определения базиса в лин. Пространстве. Каким из этих определений удобнее пользоваться при решении задач?
- •28)Размерность и базис линейного пространства. Теорема о разложении векторов по базису
- •29)Преобразование координат вектора при переходе к другому базису. Матрица перехода от одного базиса к другому
- •30)Что называют линейным подпространством в линейном пространстве?
17) Корень многочлена
Многочленом го порядка одной переменной называется функция вида
, (1)
где - заданные числа, называемые коэффициентами многочлена.
Порядок многочлена определяется максимальной степенью . Например,
1)
- многочлен 3-го порядка, т.к.
- максимальная степень в данном многочлене.
Этот многочлен имеет следующие
коэффициенты:![]()
2)
![]() - многочлен 2-го порядка. Его коэффициенты:
- многочлен 2-го порядка. Его коэффициенты:
![]()
3)
![]() -
многочлен 1-го порядка. Его коэффициенты:
-
многочлен 1-го порядка. Его коэффициенты:
![]()
4)
![]() - многочлен нулевого порядка,
- многочлен нулевого порядка,
![]() .
.
Корнями многочлена (1) называются решения уравнения
![]() .
(2)
.
(2)
Корень
многочлена (1) является корнем кратности
![]() ,
если он встречается
раз среди всех корней уравнения (2).
,
если он встречается
раз среди всех корней уравнения (2).
18) Основная теорема алгебры утверждает, что всякий отличный от константы многочлен с комплексными коэффициентами имеет по крайней мере один корень в поле комплексных чисел. (Поле комплексных чисел алгебраически замкнуто)
Доказательство:
Самое простое доказательство этой теоремы даётся методами комплексного анализа. Используется тот факт, что функция, аналитическая на всей комплексной плоскости и не имеющая особенностей на бесконечности, есть константа. Посему, функция 1/p, где p — многочлен, должна иметь хоть один полюс на комплексной плоскости, а, соответственно, многочлен имеет хоть один корень.
19. Многочлены с действительными коэффициентами. Теоремы о многочленах с действительными коэффициентами
Если
многочлен
имеет действительные коэффициенты, то
наряду с его разложением над полем
(когда
считается комплексной величиной)
возможно также разложение этого
многочлена на множестве действительных
чисел (над полем
![]() ),
когда переменная
принимает только действительные
значения, и соответственно
принимает только действительные
значения. При разложении многочлена с
действительными коэффициентами над
полем
следует помнить, что не все многочлены
второго порядка приводимы над полем
.
),
когда переменная
принимает только действительные
значения, и соответственно
принимает только действительные
значения. При разложении многочлена с
действительными коэффициентами над
полем
следует помнить, что не все многочлены
второго порядка приводимы над полем
.
Теорема Безу. Остаток от деления многочлена на многочлен равен .
Основная
теорема алгебры многочленов: любой
многочлен степени
![]() имеет ровно
корней, считая каждый корень столько
раз, какова его кратность.
имеет ровно
корней, считая каждый корень столько
раз, какова его кратность.
Согласно этой теореме любой многочлен с комплексными коэффициентами разлагается в следующее произведение
![]() ,
,
![]()
где
![]() -
все корни многочлена
-
все корни многочлена
![]() ,
имеющие кратности
,
имеющие кратности
![]() соответственно.
соответственно.
20. Понятие матрицы. Диагональные и треугольные матрицы. Транспонирование матриц. Сложение(вычитание) матриц, умножение матрицы на число. Свойства сложения матриц. Свойство умножения матрицы на число
Матрица – прямоугольная таблица чисел, содержащая строк и столбцов, записанная в круглых скобках или двойных прямых чертах.
Диагональная
матрица —
квадратная матрица,
все элементы которой, стоящие вне главной
диагонали, равны нулю. Квадратная
матрица D =
(dij),
где dij =
0 для
всяких ![]() ,
называется диагональной
матрицей.
,
называется диагональной
матрицей.
Диагональная матрица имеет вид:
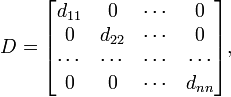
Такая матрица является одновременно и верхнетреугольной и нижнетреугольной.
Квадратная матрица называется треугольной, если под ее главной диагональю (или над ее главной диагональю) все элементы равны нулю.
Примеры треугольных матриц:
![]() -
A
- верхне-треугольные матрицы 2-го порядка,
B
- нижне-треугольная матрица 3-го порядка.
-
A
- верхне-треугольные матрицы 2-го порядка,
B
- нижне-треугольная матрица 3-го порядка.
Сложение
матриц
![]() и
и
![]() возможно только для матриц с одинаковыми
размерами и производится по правилу:
возможно только для матриц с одинаковыми
размерами и производится по правилу:
![]() ,
где
,
где
![]() .
.
![]()
Операции сложения матриц и умножение матриц на число обладают следующими свойствами:
![]() -
свойство коммутативности сложения
матриц;
-
свойство коммутативности сложения
матриц;
![]() -
свойство ассоциативности сложения
матриц;
-
свойство ассоциативности сложения
матриц;
![]() -
первый закон дистрибутивности;
-
первый закон дистрибутивности;
![]() -
второй закон дистрибутивности.
-
второй закон дистрибутивности.
Нахождение
разности
![]() матриц
матриц
![]() определяется с помощью рассмотренных
выше операций умножения матрицы на
число и сложения матриц:
определяется с помощью рассмотренных
выше операций умножения матрицы на
число и сложения матриц:
![]() .
Аналогично,
.
Аналогично,
![]() .
.
![]()
Транспонирование
матрицы. Транспонирование матрицы
обозначается
![]() и означает операцию переписывания строк
(столбцов) матрицы
в виде соответствующих столбцов (строк).
и означает операцию переписывания строк
(столбцов) матрицы
в виде соответствующих столбцов (строк).
![]()
