МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

(ФГБОУ ВПО «ВГТУ», ВГТУ)

КУРСОВАЯ РАБОТА

По дисциплине «Высшая математика»

Тема «Условный экстремум. Метод множителей Лагранжа. Моделирование и численное решение задачи об оптимальной производственной программе».

Выполнил студент АТ-101 В.М.Мугатина

Группа Подпись, инициалы, фамилия

дата

Руководитель В.С.Купцов

Подпись, инициалы, фамилия

дата

Защищена _______________________

Оценка________________________

Воронеж 2011

Содержание

Введение 3

Теоретические сведения 4

Условие курсовой работы 11

Решение 12

Вывод 17

Список литературы 18

Введение

Метод Лагранжа базируется на нескольких ключевых идеях. Одна из них состоит в том, как искать минимумы и максимумы функции, если на функцию заданы некоторые ограничения. Этот приём носит название «метод множителей Лагранжа»

Данная тема актуальна в современном мире, так как метод множителей Лагранжа применяется при решении задач нелинейного программирования, возникающих во многих областях (например, в экономике).

Важное место в математическом аппарате экономики занимают оптимальные задачи – задачи, которых ищется наилучшее в определенном смысле решение. В экономической практике требуется использовать имеющиеся ресурс наиболее выгодным образом. В экономической теории одним из отправных пунктов является постулат о том, что каждый экономический субъект, имея определенную свободу выбора своего поведения, отыскивает наилучший, со своей точки зрения, вариант. И оптимизационные задачи служат средством описания поведения экономических субъектов, инструментом исследования закономерностей этого поведения.

Теоретические сведения. Понятие условного экстремума.

Пусть на открытом множестве заданы функции

(1)

. Обозначим через множество точек , в которых все функции , обращаются в нуль:

(2)

Уравнения

(3)

называются уравнениями связи.

Определение 1. Пусть на задана функция . Точка называется точкой условного экстремума функции относительно (или при выполнении) уравнения связи (3), если она является точкой обычного экстремума этой функции, рассматриваемой только на множестве .

Иначе говоря, здесь значение функции в точке сравнивается не со всеми ее значениями в достаточно малой окрестности этой точки, а только со значениями в точках, принадлежащий достаточно малой окрестности и множеству . Как и в случае обычных экстремумов можно, естественно, рассматривать точки просто условного экстремума и точки строго условного экстремума.

Рассмотрим, например, функцию

(4)

И уравнение связи

(5)

Найдем условный экстремум функции (4) при выполнении уравнения связи (5). Из (5) имеем

.

Таким образом, при выполнении условия связи функция (4) является функцией одного переменного, ее экстремум находится элементарно: приравнивая нулю ее производную (необходимое условие экстремума), получим 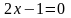, откуда . В этой точке функция (4), очевидно, имеет минимум (она является многочленом второй степени с положительным коэффициентом при старшем члене). Значению согласно уравнению связи (5) соответствует .

Следовательно, в точке функция (4) достигает минимума относительно уравнения связи (5). Геометрически это означает, что точка параболоида 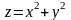, находящаяся над точкой , является самой низкой из всех его точек, лежащих над прямой (5).

Предполагают, что

1. Функции и имеют непрерывные частные производные первого порядка на открытом множестве .

2. и ранг матрицы в каждой точке множества _равен , т.е. числу строк.

Это означает, что функции системы (1) независимы в любой окрестности каждой точки .

_Пусть ; согласно условию 2, в точке _{хоть один из определителей вида}

_{отличен от нуля; пусть для определенности в точке}

_{. (6)}

_{Тогда в силу теоремы о неявных функциях систему уравнений (3) в некоторой окрестности точки можно разрешить относительно переменных :}

₍₇₎

_{Подставляя (7) в функцию , получим функцию}

₍₈₎

_{от переменных} , определенную и непрерывную дифференцируемую в некоторой окрестности точки .

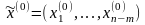_{Точка является точкой (строгого) условного экстремума для функции относительно уравнения связи (3) в том и только том случае, когда точка является точкой обычного (строгого) экстремума для функции (8). Это непосредственно следует из того, что условия (3) и (7) равносильны.}