15. Вычисление ранга матрицы методом элементарных преобразований.

II. Метод элементарных преобразований

Элементарными преобразованиями матрицы называют следующие:

1. Перестановка строк (столбцов).

2. Умножение строки (столбца) на число, отличное от нуля.

3. Прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на некоторое число.

4. Вычёркивание строки (столбца), все элементы которой равны нулю.

З а м е ч а н и е . 1) Элементарные преобразования не меняют ранга матрицы; 2) матрицы, полученные одна из другой путём элементарных преобразований, называются эквивалентными (обозначаются A ~В).

Чтобы вычислить ранг матрицы А, путём элементарных преобразований сводим её к ступенчатому виду (в частности к треугольному), выделяя наибольший минор, отличный от нуля.

A~

rangA = rangB= k

Пример 2. Найти ранг матрицы

Решение. 1) переставим строки матрицы: 

2) первую строку умножим на 2 и сложим со второй:  ,

3)  первую строку умножим на 3 и сложим с третьей, одновременно вторую строку   прибавим к четвёртой:

,

4) умножим вторую строку на   ,  третью на   , пятую на   ,четвёртую вычеркнем :

,

5) прибавим вторую строку к третьей и четвёртой:

~  ,

Ранг последней матрицы, а значит и исходной, равен двум: rangA = 2.

Пример 3. Найти ранг матрицы

rang A=2

Над матрицей А были проведены следующие преобразования:

а) Первая строка матрицы А умножается на (- 2) и прибавляется ко второй.

б ) Первая строка матрицы А умножается на (- 1) и прибавляется к последней.

в) Вторая строка матрицы А умножается на (- 2) и прибавляется к третьей.

г) Нулевая строка вычёркивается.

Оставшаяся матрица содержит миноры второго порядка отличные от нуля. Строки такой матрицы называются линейно независимыми, их число равно рангу матрицы

16. Теорема Кронекера-Капелли. Решение систем на основе теоремы Кронекера-Капелли.

Теорема Кронекера-Капелли

Матрица, получающаяся конкатенацией матрицы   и столбца правых частей 

называется расширенной матрицей системы линейных уравнений.

Т

Теорема [Кронекер, Капелли]. Система совместна тогда и только тогда, когда ранг матрицы этой системы совпадает с рангом ее расширенной матрицы:

При выполнении этого условия, система имеет единственное решение, если число неизвестных   совпадает с общим значением ранга  , и бесконечное множество решений, если   меньше этого значения.

Доказательство необходимости. Пусть существует решение   системы, тогда

т.е. столбец   линейно выражается через столбцы  . Но тогда

Следовательно  .

Доказательство достаточности проводится в следующем пункте. ♦

§

Обозначение   для ранга матрицы   соответствует по смыслу этому же обозначению в методе Гаусса: после приведения к трапециевидному (или треугольному) виду в системе л.у. должно остаться ровно   линейно независимых уравнений, явно содержащих неизвестные. Это утверждение вытекает из способа вычисления ранга матрицы по методу элементарных преобразований.

П

Пример. Исследовать совместность системы уравнений

в зависимости от значения параметра  .

Решение. В этом примере число уравнений совпадает с числом неизвестных. Это обстоятельство несколько облегчает рассуждения. Обратимся к замечанию из предыдущего пункта: система л.у. с числом уравнений, совпадающем с числом неизвестных, как правило, совместна. Тогда попробуем установить условия, обеспечивающие противоположное свойство — несовместность. Оно, фактически, единственно: за все отвечает определитель системы  . Если он отличен от нуля — система совместна.

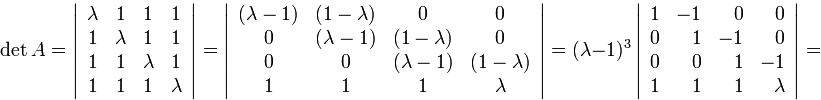
. По теореме Крамера при   и при   решение системы единственно:

Осталось исследовать критические случаи:   и  : определитель системы обращается в нуль, но система может оказаться совместной. Придется вычислять ранги, но, к счастью, уже числовых матриц (а не зависящих от параметра, как исходная!). При   имеем

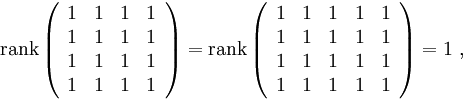
и система совместна. Она эквивалентна единственному уравнению

которое имеет бесконечно много решений.

При  :

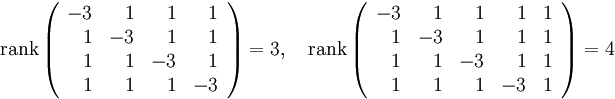
и система несовместна.

Ответ. Система несовместна при  ; она имеет бесконечное множество решений при   и единственное решение при  .

!

Что можно сказать о совместности или несовместности случайным образом составленной системы из   линейных уравнений относительно  неизвестных? При   система, как правило, совместна и имеет бесконечное множество решений. В самом деле, если выбрать минор порядка   в матрице системы  , элементы которой считаются случайными, то этот минор будет «с вероятностью 1» отличен от нуля (см. рассуждения в предыдущем пункте о совместности системы л.у. при  ). Таким образом,  , и автоматически получаем, что   (поскольку ранг не может больше количества строк матрицы). Если же   то такаяпереопределенная система, как правило, несовместна. Рассуждения для доказательства правдоподобия этого утверждения могут быть следующими. Выберем произвольным образом в рассматриваемой системе какую-то подсистему, состоящую из   уравнений. Она, как правило, будет иметь единственное решение. Теперь составим другую подсистему, хотя бы одним уравнением отличающуюся от предыдущей (поскольку   такое всегда можно сделать). Новая подсистема снова, как правило, будет иметь единственное решение. Однако решения этих двух подсистем будут, как правило, различными и, следовательно, сама основная система не будет иметь решения. В этом последнем случае переопределенной системы имеется, однако, важный исключительный, который рассмотрим ☞ НИЖЕ.

=>

Система однородных уравнений

всегда совместна: она имеет тривиальное решение  . Для того, чтобы у нее существовало еще и нетривиальное решение необходимо и достаточно, чтобы определитель ее матрицы был равен нулю.

П

Пример. Найти условие, при котором три точки плоскости с координатами   и   лежат на одной прямой.

Решение. Будем искать уравнение прямой в виде   при неопределенных коэффициентах  . Если точки лежат на прямой, то получаем для определения этих коэффициентов систему линейных уравнений:

Получившаяся система является однородной, условие существования у нее нетривиального решения (т.е. набора   при хотя бы одном из чисел отличном от нуля):

?

Доказать, что для совместности системы

необходимо, чтобы было выполнено условие

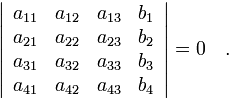
Является ли это условие достаточным для совместности?

И

Исторический комментарий. Понятие ранга матрицы и результат, известный в литературе как «теорема Кронекера–Капелли», были открыты несколькими независимыми исследователями. Первое доказательство этой теоремы принадлежит Ч.Л.Додсону, оно было напечатано им в 1867 г. в книге

Источник.  An elementary treatise on determinants

в следующей формулировке.

Теорема. Для того чтобы система   неоднородных уравнений была совместна, необходимо и достаточно, чтобы порядок наибольшего отличного от нуля минора был одинаков в расширенной и нерасширенной матрице системы.