
- •1. Матрицы и действия над ними.
- •2. 1 2 3 И n порядок
- •3. Свойства определителей.
- •4. Разложение определителя по строке или столбцу.
- •5. Определитель произведения матриц.
- •6. Формулы Крамера для решения системы линейных уравнений.
- •7. Обратная матрица и ее вычисление.
- •Свойства обратной матрицы
- •8. Свойства обратной матрицы и новый вывод формул Крамера.
- •9. Определение n-мерных арифметических векторов и действий над ними.
- •10. Линейная зависимость и независимость векторов.
- •11. Максимальная линейно независимая подсистема векторов. Линейная зависимость векторов
- •Свойства систем векторов
- •12. Определение ранга матрицы. Теорема о ранге матрицы.
- •13. Теорема о равенстве числа векторов в двух максимальных линейно независимых подсистемах векторов.
- •14. Вычисление ранга матрицы методом окаймляющих миноров. Метод окаймляющих миноров
- •15. Вычисление ранга матрицы методом элементарных преобразований.
- •II. Метод элементарных преобразований
- •16. Теорема Кронекера-Капелли. Решение систем на основе теоремы Кронекера-Капелли.
- •17. Однородная система линейных уравнений. Свойства ее решений.
- •18. Фундаментальная система решений однородной системы линейных уравнений и теорема о числе решений в ее составе.
- •19. Связь решений линейной неоднородной и соответствующей ей однородной систем.
- •20. Метод Гаусса решения линейных уравнений.
- •§ 3. Декартова система координат в пространстве
- •§ 1. Декартова система координат на плоскости
- •22. Полярные координаты на плоскости и их связь с декартовыми прямоугольными координатами.
- •§ 2. Полярная система координат на плоскости
- •23. Понятие свободного вектора. Теорема о проекции вектора на ось.
- •Свободный вектор
- •24. Координаты вектора и их вычисление по координатам его начала и конца. Направляющие косинусы.
- •25. Длина вектора и формула для вычисления расстояния между двумя точками пространства.
- •1.6. Расстояние между двумя точками
- •26. Линейные операции над векторами. Линейные операции над векторами
- •27. Основные теоремы о проекциях векторов.
- •28. Разложение векторов на компоненты.
- •29. Скалярное произведение векторов и его свойства.
- •Геометрический смысл скалярного произведения векторов
- •Алгебраические свойства скалярного произведения
- •Геометрические свойства скалярного произведения
- •30. Векторное произведение векторов и его свойства.
- •Алгебраические свойства векторного произведения
- •Геометрические свойства векторного произведения
- •Выражение векторного произведения через координаты векторов
- •31. Смешанное произведение векторов и его свойства.
- •1.16. Смешанное произведение векторов и его свойства
- •Геометрические свойства смешанного произведения
- •Алгебраические свойства смешанного произведения
- •32. Общее уравнение прямой на плоскости.
- •33. Уравнение прямой в отрезках.
- •34. Нормальное уравнение прямой. Вычисление расстояния от точки до прямой на плоскости. Общее уравнение прямой
- •35. Общее уравнение плоскости.
- •36. Уравнение плоскости в отрезках.
- •37. Нормальное уравнение плоскости, Расстояние от точки до плоскости.
- •38. Канонические уравнения прямой.
- •39. Эллипс: уравнение, общий вид и свойства кривой.
33. Уравнение прямой в отрезках.
Уравнение прямой в отрезках
Пусть
на координатных осях заданы точки ![]() и
и ![]() ,
причем
,
причем ![]() (рис.3.19).
Требуется составить уравнение прямой,
проходящей через эти точки.
(рис.3.19).
Требуется составить уравнение прямой,
проходящей через эти точки.
Подставляя
в уравнение (3.16) ![]() ,
получаем:
Меняя
левую и правую части равенства, получаем
уравнение
,
получаем:
Меняя
левую и правую части равенства, получаем
уравнение
![]() которое
называется уравнением
прямой "в отрезках".
Говорят, что прямая, проходящая через
точки
и
,
отсекает на координатных осях
"отрезки":
которое
называется уравнением
прямой "в отрезках".
Говорят, что прямая, проходящая через
точки
и
,
отсекает на координатных осях
"отрезки": ![]() на
оси абсцисс и
на
оси абсцисс и ![]() на
оси ординат. Разумеется, длины
отрезков
на
оси ординат. Разумеется, длины
отрезков ![]() и
и ![]() равны
равны ![]() и
и ![]() соответственно.
соответственно.
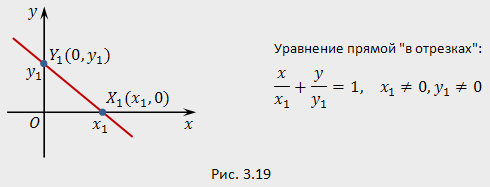
34. Нормальное уравнение прямой. Вычисление расстояния от точки до прямой на плоскости. Общее уравнение прямой
Ненулевой вектор , перпендикулярный заданной прямой, называется нормальным вектором (или, короче, нормалью) для этой прямой.
Пусть
на координатной плоскости ![]() (в
прямоугольной системе координат) заданы:
(в
прямоугольной системе координат) заданы:
а)
точка ![]() ;
;
б)
ненулевой вектор ![]() (рис.3.5,а).
(рис.3.5,а).
Требуется составить уравнение прямой, проходящей через точку перпендикулярно вектору .
Выберем
на плоскости произвольную точку ![]() .
Обозначим
.
Обозначим ![]() и
и ![]() —
радиус-векторы точек
и
.
Точка
—
радиус-векторы точек
и
.
Точка ![]() принадлежит
заданной прямой тогда и только тогда,
когда векторы
принадлежит
заданной прямой тогда и только тогда,
когда векторы ![]() и
перпендикулярны
(рис.3.5,б). Условие ортогональности
запишем при помощи скалярного произведения
(см. разд. 1.6.2):
и
перпендикулярны
(рис.3.5,б). Условие ортогональности
запишем при помощи скалярного произведения
(см. разд. 1.6.2):
![]() Учитывая,
что
Учитывая,
что ![]() ,
получаем векторное
уравнение прямой:
,
получаем векторное
уравнение прямой:
![]() Это
уравнение можно записать в другой форме.
Преобразуем левую часть ,
используя свойства скалярного произведения
(см. ). Обозначая
Это
уравнение можно записать в другой форме.
Преобразуем левую часть ,
используя свойства скалярного произведения
(см. ). Обозначая ![]() ,
получаем уравнение
,
получаем уравнение
![]() или
или ![]() выражающее
постоянство проекций на
нормаль
радиус-векторов
точек, принадлежащих прямой.
выражающее
постоянство проекций на
нормаль
радиус-векторов
точек, принадлежащих прямой.

Получим
координатную форму записи векторного
уравнения прямой (3.5). Так как ![]() и
и ![]() ,
по формуле (1.9) находим
,
по формуле (1.9) находим ![]() или
или
![]() Полученное
соотношение (3.7) позволяет по координатам
точки
и
координатам
Полученное
соотношение (3.7) позволяет по координатам
точки
и
координатам ![]() нормали
записать
уравнение прямой без промежуточных
вычислений.
нормали
записать
уравнение прямой без промежуточных
вычислений.
Обозначив ![]() ,
получим уравнение
,
получим уравнение
![]() которое
называется общим
уравнением прямой на плоскости.
Поскольку коэффициенты
и
не
равны нулю одновременно (это координаты
ненулевого вектора
),
уравнение (3.8) является алгебраическим
уравнением первой степени, т.е. линейным
уравнением с двумя неизвестными.
Следовательно, прямая является
алгебраической линией первого порядка.
которое
называется общим
уравнением прямой на плоскости.
Поскольку коэффициенты
и
не
равны нулю одновременно (это координаты
ненулевого вектора
),
уравнение (3.8) является алгебраическим
уравнением первой степени, т.е. линейным
уравнением с двумя неизвестными.
Следовательно, прямая является
алгебраической линией первого порядка.
Проводя рассуждения в обратном порядке, делаем вывод о том, что линейное уравнение (3.8) задает на координатной плоскости прямую. Полученные выводы сделаны для прямоугольной системы координат, но, учитывая теорему 3.1 (см. ), они переносятся (без изменений) и на любую аффинную систему координат.
35. Общее уравнение плоскости.
Рассмотрим
произвольную точку
![]() в
пространстве и некоторый вектор
в
пространстве и некоторый вектор
![]() Очевидно,
что геометрическим местом точек
Очевидно,
что геометрическим местом точек
![]() таких,
что вектор
таких,
что вектор
![]() перпендикулярен
вектору
перпендикулярен
вектору
![]() будет
плоскость, проходящая через точку M
перпендикулярно прямой, для которой
вектор
будет
плоскость, проходящая через точку M
перпендикулярно прямой, для которой
вектор
![]() является
направляющим. Нашей задачей будет
установить уравнение плоскости, то есть
найти соотношение, которому удовлетворяют
координаты точки A.
является
направляющим. Нашей задачей будет
установить уравнение плоскости, то есть
найти соотношение, которому удовлетворяют
координаты точки A.
Запишем условие перпендикулярности векторов с использованием скалярного произведения:
|
Запишем последнее равенство в координатах:
|
Поскольку все наши выкладки были равносильными, то это и есть уравнение плоскости, проходящей через заданную точку. Преобразуем его к виду
|
Обозначая
![]() получим
получим
|
Это и есть так называемое общее уравнение плоскости.
Определение 9.19.
Вектор
![]() называется
нормальным
вектором
(или просто нормалью)
для плоскости, заданной общим уравнением
(1).
называется
нормальным
вектором
(или просто нормалью)
для плоскости, заданной общим уравнением
(1).
Нормальный вектор к плоскости перпендикулярен ей, что следует из самого вывода уравнения плоскости.
Рассмотрим
плоскость 3x
+ 2y
+ z
– 6 = 0. Пусть A
– точка пересечения этой плоскости с
осью Ox,
то есть A(2;
0; 0). Точка B(0;
3; 0) – это точка пересечения данной
плоскости с осью Oy,
точка C(0;
0; 6) – с осью Oz
(чертеж 9.7.1). Уравнение
 называется
уравнением
плоскости в отрезках на осях.
называется
уравнением
плоскости в отрезках на осях.
Эта плоскость пересекает оси Ox, Oy, Oz соответственно в точках A(a; 0; 0), B(0; b; 0), C(0; 0; c).
Плоскость,
изображенная на чертеже 9.7.1, имеет такое
уравнение в отрезках на осях:

Общее уравнение плоскости
![]() ,
где вектор
нормали к плоскости -
,
где вектор
нормали к плоскости - ![]() .
.
