1.6. Расстояние между двумя точками

 Если нам известны координаты точек (естественно, в заданной системе координат), то однозначно известно их положение. Поэтому можно найти любые геометрические характеристики их взаимного расположения. Получим формулы, позволяющие по известным координатам двух точек вычислить расстояние между ними.  В простейшем случае, когда две точки А₁ и А₂ находятся на одной оси, расстояние между ними определяется формулой

s = |x₂ − x₁|, (3)

где х₁, х₂ − координаты точек А₁ и А₂ соответственно.  Очевидно, что расстояние от А₁ до А₂ равно расстоянию от А₂ до А₁, что и привело у к тому, что в формуле (3) появился знак модуля числа.  Пусть на плоскости задана система координат ХОY, в которой координаты точки А₁ равны х₁ и у₁, а координаты точки А₂, соответственно, равны х₂ и у₂ (рис. 8).

рис. 8

 В прямоугольном треугольнике А₁А₂В длина стороны А₂В равна |х₂ − х₁|, а длина стороны А₁В = |у₂ − у₁|, поэтому расстояние между точками А₁ и А₂ можно найти по теореме Пифагора:

s = √{(x₂ − x₁)² + (y₂ − y₁)²}. (4)

26. Линейные операции над векторами. Линейные операции над векторами

Сложение векторов

Пусть даны два вектора   и  . Приложим вектор   к точке   (концу вектора  ) и получим вектор   (рис.1.7,а; здесь и далее равные векторы отмечены одинаковыми засечками). Вектор   называется суммой векторов   и   и обозначается  . Это нахождение суммы называется правилом треугольника.

Сумму двух неколлинеарных векторов   и   можно найти по правилу параллелограмма. Для этого откладываем от любой точки  векторы   и  , а затем строим параллелограмм   (рис. 1.7,6). Диагональ   параллелограмма определяет сумму:  .

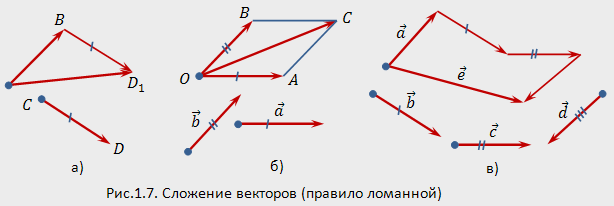
Для нахождения суммы нескольких векторов можно построить ломаную из равных им векторов. Тогда замыкающий вектор, соединяющий начало первого вектора ломаной с концом последнего ее вектора, равен сумме всех векторов ломаной. На рис.1.7,в изображена сумма   четырех векторов  . Таким способом (правило ломаной) можно сложить любое конечное число векторов. Заметим, что сумма векторов не зависит от точек приложения слагаемых и от порядка суммирования. Например, "выстраивая цепочку" векторов для суммы в виде  , получим вектор, равный вектору  . Если ломаная получилась замкнутой, то сумма равна нулевому вектору.

Вычитание векторов

Вектор   называется противоположным вектору  , если их сумма равна нулевому вектору:  . Противоположный вектор   имеет длину  , коллинеарен и противоположно направлен вектору   (рис.1.8,а,б). Нулевой вектор является противоположным самому себе.

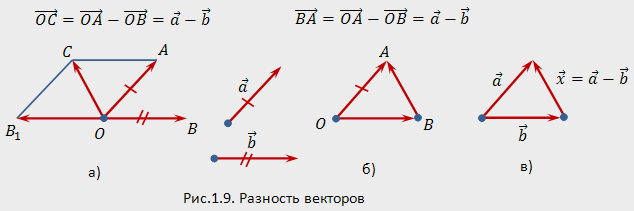
Разностью векторов   и   называется сумма вектора   с вектором  , противоположным вектору  :

Для нахождения разности векторов   и   приложим к произвольной точке   векторы  , а также вектор  , противоположный вектору   (рис.1.9,а). Искомую разность находим по правилу параллелограмма:

Для нахождения разности проще использовать правило треугольника (рис. 1.9,6). Для этого прикладываем к произвольной точке   векторы  . Вектор   при этом равен искомой разности  .

Вычитание векторов — действие, обратное сложению — можно определить также следующим образом: разностью векторов   и  называется такой вектор  , который в сумме с вектором   дает вектор   (рис.1.9,в), т.е. разность   — это решение уравнения  .

Пример 1.2. Для векторов на рис. 1.6 найти следующие суммы и разности:

Решение. Учитывая равенство  , получаем по правилу треугольника  .

Поскольку   и  , то  .

По правилу параллелограмма  .

Так как   и  , находим 

Умножение вектора на число

Произведением ненулевого вектора а на действительное число   называется вектор  , удовлетворяющий условиям:

1) длина вектора   равна  , т.е.  ;

2) векторы   и   коллинеарные  ;

3) векторы   и   одинаково направлены, если  , и противоположно направлены, если  .

Произведение нулевого вектора на любое число   считается (по определению) нулевым вектором:  ; произведение любого вектора на число нуль также считается нулевым вектором:  . Из определения произведения следует, что:

а) при умножении на единицу   вектор не изменяется:  ;

б) при умножении вектора на   получается противоположный вектор:  ;

в) деление вектора на отличное от нуля число   сводится к его умножению на число  , обратное  .

г) при делении ненулевого вектора   на его длину, т.е. при умножении   на число   получаем единичный вектор, одинаково направленный с вектором  .

Действительно, длина вектора   равна единице:  .

Вектор   коллинеарен и одинаково направлен с вектором  , так как  ;

д) при умножении единичного вектора на число   получаем коллинеарный ему вектор, длина которого равна  .

На рис.1.10 изображены векторы, получающиеся в результате умножения данного вектора   на   и  , а также противоположный вектор  .

Свойства линейных операций над векторами

Сложение векторов и умножение вектора на число называются линейными операциями над векторами. Для любых векторов   и любых действительных чисел   справедливы равенства:

Свойства 1, 2 выражают коммутативность и ассоциативность операции сложения векторов, свойство 5 — ассоциативность операции умножения на число, свойства 6,7 — законы дистрибутивности, свойство 8 называется унитарностью.