23. Понятие свободного вектора. Теорема о проекции вектора на ось.

Закрепленный вектор (направленный отрезок) — упорядоченная пара точек. Первая называется началом вектора, вторая концом.

Закрепленный вектор с началом в точке A и концом в точке B обозначается  .

Вектор, у которого начало и конец совпадает, называется нулевым и обозначается  .

Длина вектора (модуль или абсолютная величина) — расстояние между его началом и концом, обозначается  .

Два закрепленных вектора называются коллинеарными, если они параллельны одной и той же прямой. Нулевой вектор считается параллельным (а значит, и коллинеарным) любому вектору.

Три закрепленных вектора называются компланарными, если они параллельны одной и той же плоскости.

Свободный вектор

Закрепленные векторы называются равными, если они коллинеарны, одинаково направлены и имеют равные длины.

Необходимо заметить, что равенство векторов отличается от привычного равенства чисел. Если число равно другому числу, то эти числа совпадают, на самом деле, это одно и то же число. Если закрепленный вектор равен другому вектору, они могут не совпадать. Иногда равенство векторов называют эквиполлентностью.

Основные свойства равенства векторов:

1. рефлексивность:  ;

2. симметричность: если 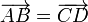 , то  ;

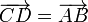3. транзитивность: если   и  , то  .

Отношение, обладающее данными свойствами, называется отношением эквивалентности.

Таким образом, существует множество несовпадающих закрепленных векторов, которые равны между собой. Во многих задачах безразлично какой из равных векторов рассматривать. В этих случаях говорят о свободном векторе. Под свободным вектором можно понимать любой из равных между собой векторов. Свободный вектор чаще всего обозначаются полужирными строчными латинскими буквами.

Теорема 3. Проекция вектора   на ось (направленная прямая) l равна произведению длины вектора   на косинус угла между направлением вектора и направлением оси, т.е.    = a  cos ,  = ( , l).

24. Координаты вектора и их вычисление по координатам его начала и конца. Направляющие косинусы.

[AB]=sqrt((Xb-Xa)^2+(Yb-Ya)^2+(Zb-Za)^2)

Направляющие косинусы вектора (в пространстве) – это косинусы углов, которые вектор образует с положительными полуосями координат. Направляющие косинусы однозначно задают направление вектора. Если вектор имеет длину 1, то его направляющие косинусы равны его координатам. В общем случае для вектора с координатами (a; b; c) направляющие косинусы равны:

где a, b, g – углы, составляемые вектором с осями x, y, z соответственно.

Сумма квадратов направляющих косинусов равна 1.

25. Длина вектора и формула для вычисления расстояния между двумя точками пространства.

Длина вектора

Понятие вектора

Отрезок, для которого указано, какой из его концов считается началом, а какой — концом, называется вектором. Направление вектора (от начала к концу) на рисунках отмечается стрелкой. Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления. Нулевой вектор обозначается символом 

Длиной ненулевого вектора   называется длина отрезка AB. Длина вектора  (вектора  ) обозначается так:    . Длина нулевого вектора считается равной нулю:  . Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой ил на параллельных прямых. Если два ненулевых вектора   и   коллинеарны и если при этом лучи AB и CD сонаправлены, то векторы   и   называются сонаправленными, а если эти лучи не являются сонаправленными, то векторы   и   называютсяпротивоположно направленными. Нулевой вектор принято считать сонаправленным с любим вектором.