
- •37. Первый замечательный предел.
- •38. Сравнение бесконечно малых величин
- •42. Производная степенной функции.
- •43 Производная алгебраической суммы функций
- •44. Производная частного функций.
- •45. Теорема (о дифференцировании обратной функции)
- •46. Теорема сложной функции
- •47. Производные высших порядков явно заданной функции
- •48 Понятие дифференциала функции
- •49 Применение дифференциала к приближенным вычислениям
- •50. Функция, заданная параметрически
- •53. Теорема (правило Лопиталя).
- •54. Раскрытие неопределенностей с использованием правила Лопиталя
37. Первый замечательный предел.
Так называют легко выводимую в курсе математического анализа формулу
![]() ,
,
где аргумент х измеряется в радианах. Из первого замечательного предела следует эквивалентность при х →0 следующих бесконечно малых величин: ах, sinax; tgax; arcsinax; arctgax. Это означает, что предел отношения двух любых из этих функций при х →0 равен 1.
38. Сравнение бесконечно малых величин
Зададимся вопросом, как можно сравнить две бесконечно малые величины или две бесконечно большие величины?
Определения.
Пусть при ![]() функции f(x)
и g(x) являются бесконечно малыми.
Тогда:
функции f(x)
и g(x) являются бесконечно малыми.
Тогда:
2.
Если ![]() ,
то f(x) называется бесконечно
малой высшего порядка относительно
g(x).
,
то f(x) называется бесконечно
малой высшего порядка относительно
g(x).
2.
Если ![]() (конечен
и отличен от 0), то f(x) называется
бесконечно малой n-го порядка относительно
g(x).
(конечен
и отличен от 0), то f(x) называется
бесконечно малой n-го порядка относительно
g(x).
3.
Если ![]() ,
то f(x) и g(x) называются эквивалентными
бесконечно малыми.Эквивалентность
записывается так:
,
то f(x) и g(x) называются эквивалентными
бесконечно малыми.Эквивалентность
записывается так: ![]() .
.
Свойства эквивалентных бесконечно малых:
1. Разность двух эквивалентных бесконечно малых есть бесконечно малая высшего порядка относительно каждой из них.
2. Если из суммы нескольких бесконечно малых разных порядков отбросить бесконечно малые высших порядков, то оставшаяся часть, называемая главной, эквивалентна всей сумме.
Из
первого свойства следует, что эквивалентные
бесконечно малые могут сделаться
приближенно равными со сколь угодно
малой относительной погрешностью.
Поэтому знак ![]() мы
применяем как для обозначения эквивалентности
бесконечно малых, так и для записи
приближенного равенства их достаточно
малых значений.
мы
применяем как для обозначения эквивалентности
бесконечно малых, так и для записи
приближенного равенства их достаточно
малых значений.
39. Непрерывность функции |
Определение. Функция Определение
непрерывности по Коши (нотация Рассмотрим
функцию f (x), которая отображает
множество действительных чисел
выполняется неравенство
Пример
2. Доказать непрерывность функции Решение. Для
доказательства найдем приращение
функции
Найдем
предел приращения функции при
Так
как предел приращения функции
при
равен
нулю, то функция при |
40. Определение. Точка х0 называется точкой разрыва функции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке.
Классификация точек разрыва функции
Все точки разрыва функции разделяются на точки разрыва первого и второго рода.
Определение. Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.
Определение. Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.

41. Определение производной Определение: Пусть функция y=f(x) определена в точке x и в некоторой ее окрестности. Дадим аргументу x приращение x, такое, чтобы не выйти из указанной окрестности. Найдем соответствующее приращение функции y и составим отношение. Если существует предел этого отношения при x0, то указанный предел называют производной функции y=f(x) в точке x и обозначают f `(x).
![]()
Дифференци́руемая фу́нкция — это функция, имеющая дифференциал. Дифференцируемая функция может быть хорошо приближена линейной функцией. Дифференцируемость является одним из фундаментальных понятий в математике и имеет большое число приложений как внутри неё, так и в естественных науках, широко использующих математический аппарат (на данном отрезке).
Непрерывность дифференцируемой функции
Теорема 1. Пусть функция y = f(x) дифференцируема на интервале (a, b). Тогда функция f непрерывна на (a, b).
Доказательство:
Возьмем
произвольное фиксированное число x ![]() (a,b).
(a,b).
По условию теоремы
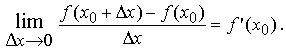
Следовательно,
в малой окрестности числа x0 можно
определить функцию α = α(Δx), стремящуюся
к нулю при ![]() такую,
что
такую,
что
![]()
Но
тогда ![]() и,
следовательно, функция f непрерывна
при x = x0. Так как число x0 –
произвольное, то функция fнепрерывна
на всем интервале (a, b).
и,
следовательно, функция f непрерывна
при x = x0. Так как число x0 –
произвольное, то функция fнепрерывна
на всем интервале (a, b).
