
- •Функции алгебры логики
- •16. В каком столбце таблицы находятся значения функции ↔ 4
- •Содержательное исчисление высказываний
- •Формулы алгебры высказываний. Формальное исчисление высказываний
- •50. Каким из ниже перечисленных слов следует заменить символ ▼ в следующем определении.
- •Логика предикатов
- •Формулы логики предикатов
- •Теория алгоритмов.
- •101. Каким из ниже перечисленных слов следует заменить символ ▼ в следующем определении.
- •102. Каким из ниже перечисленных слов следует заменить символ ▼ в следующем определении.
- •103. Каким из ниже перечисленных слов следует заменить символ ▼ в следующем определении.
- •106. Каким из ниже перечисленных слов следует заменить символ ▼ в следующем определении.
Теория алгоритмов.
101. Каким из ниже перечисленных слов следует заменить символ ▼ в следующем определении.
Функция f(x1, . . ., хп) называется ▼, если существует алгоритм, позволяющий вычислять ее значения для тех наборов аргументов, для которых она определена, и работающий вечно, если функция для данного набора значений аргументов не определена. вычислимой
102. Каким из ниже перечисленных слов следует заменить символ ▼ в следующем определении.
Множество М называется ▼, если имеется алгоритм для выяснения того, принадлежит или не принадлежит произвольный элемент к этому множеству. разрешимым.
103. Каким из ниже перечисленных слов следует заменить символ ▼ в следующем определении.
Множество M, являющееся подмножеством натуральных чисел, называется ▼, если М либо пусто, либо есть область значений некоторой вычислимой функции. перечислимым.
104. Применение к слову 138578926 Марковской подстановки (85789, 00) дает результат: 130026
105 Применение к слову шрам Марковской подстановки (ра, ар) дает результат: шарм
106. Каким из ниже перечисленных слов следует заменить символ ▼ в следующем определении.
Упорядоченный
конечный список формул подстановок
в алфавите А:

называется ▼ нормального алгоритма в А. схемой
107. Пусть А={ a0,
a1,
a2,…..,
an,
} –алфавит. Рассмотрим
схему нормального алгоритма

В какое
слово она перерабатывает слово ana0a1a2
?

108.Завершите формулировку принципа нормализации Маркова:
Для нахождения значений функции, заданной в некотором алфавите, тогда и только тогда существует какой-нибудь алгоритм, когда функция нормально вычислима
109. Дана система команд машины Тьюринга:
q1a1→q2λR;
q1a2→q3λR;
q2a2→q3λR;
q3a2→q1λR;
q3a1→q4TE;
и лента с записью: а1 а2 а2 а1 а1; начальное состояние: q1. Данная машина: зациклится.
110. Рассмотрим машину Тьюринга с алфавитом A={1,*, λ} и системой команд ………….
Какую операцию в унарном коде выполняет эта машина сложение двух натуральных чисел
111. Рассмотрим машину Тьюринга с алфавитом A={1,*, λ,0} и системой команд (*таблица*)
Какую операцию в унарном коде выполняет эта машина. копирование
112. В теории рекурсивных функций в качестве набора операторов, с помощью которых строятся новые функции, выбраны следующие наборы: оператор суперпозиции, оператор примитивной рекурсии, оператор минимизации;
113.:
Выразить функцию s(x,y)=
x
+ y
через простейшие функции с помощью
оператора примитивной рекурсии
s(x,0)=
114. С
помощью ограниченного оператора
минимизации, простейшие и
примитивно-рекурсивные функции s(x,y)=
x
+ y
и p(x,y)=
x y
выразите целую часть
y
выразите целую часть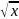 .
.
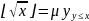 (p(S(y))>x)
(p(S(y))>x)
115. Завершите формулировку тезиса Черча:
Всякая функция, вычислимая некоторым алгоритмом, частично-рекурсивна
116.Для указанных классов функций, заданных на множестве натуральных чисел и принимающих натуральные значения, справедливо следующее утверждение: все три класса (класс всех функций, вычислимых по Тьюрингу, класс всех нормально вычислимых функций, класс всех рекурсивных функций) совпадают.
117.Рассмотрим
следующую функцию
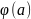 на словах в алфавите A1
={1}.
на словах в алфавите A1
={1}.
Для
произвольного слова
 длины п
в
алфавите A1
={1}
положим:
длины п
в
алфавите A1
={1}
положим:

Тогда функция не вычислима по Тьюрингу
118. Проблема распознавания самоприменимых машин Тьюринга алгоритмически неразрешима
119.Класс (f)
содержит алгоритмы, сложность которых
растёт по
крайней мере так же быстро, как данная
функция f
(f)
содержит алгоритмы, сложность которых
растёт по
крайней мере так же быстро, как данная
функция f
120. Класс NP содержит задачи, для которых алгоритмы, способные решить их за разумное время не известны
