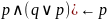Функции алгебры логики

1. Булевская переменная – это переменная, которая принимает только одно из следующих значений: 0 или 1

2. Булевская функция – это такая функция одного или нескольких булевских переменных, которая принимает только одно из следующих значений: 0 или 1

3. Число всевозможных наборов из 5 булевских переменных равно 32

4. Число всевозможных наборов из 7 булевских переменных равно 128

5. Число всевозможных булевских функций от 2 переменных равно 16

6. Число всевозможных булевских функций от 3 переменных равно 256

7. Булевская функция f(x₁,…,x _n) называется самодвойственной, если справедлива формула

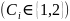
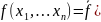
8. Булевская функция f(x₁,…,x _n) называется линейной, если она может быть выражена следующим образом

f(x₁,…,x _n )=C₀ Å C₁x₁ Å … Å C _n x _n

9. Если система булевских функций является функционально полной, то она необходимо содержит: функцию, не являющуюся самодвойственной

10.Система ∑ булевских функций является функционально полной: ∑={стрелка Пирса}

11. Если система булевских функций является функционально полной, то она необходимо содержит: функцию, не являющуюся монотонной

12.Система ∑ булевских функций является функционально полной: ∑={штрих Шеффера}

13.В каком столбце таблицы находятся значения дизъюнкции 2

14. В каком столбце таблицы находятся значения функции Å 1

15. В каком столбце таблицы находятся значения функции ↑ 3

16. В каком столбце таблицы находятся значения функции ↔ 4

17.СДНФ для функции ↔ имеет вид:

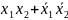
18.СДНФ для функции ↑ имеет вид:

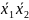
19.СДНФ для функции Å имеет вид: +

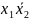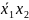
20. СДНФ для функции дизъюнкции имеет вид:

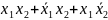
Содержательное исчисление высказываний

21.Под высказыванием понимается утвердительное предложение, которое может быть либо истинным, либо ложным, но не то и другое одновременно

22.Переменные, вместо которых можно подставлять высказывания, называют пропозициональными переменными.

23.Формула, выражающая Закон исключения третьего, имеет вид

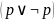
24.Формула, выражающая Закон отрицания противоречия, имеет вид

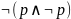
25.Формула, выражающая Закон двойного отрицания, имеет вид

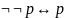
26.Формула, выражающая Закон тождества, имеет вид

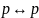
27.Формула, выражающая Закон контрапозиции, имеет вид

28.Формула, выражающая правило цепного заключения, имеет вид

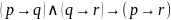
29. Формула, выражающая правило «истина из чего угодно», имеет вид

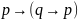
30. Формула, выражающая правило «из ложного что угодно», имеет вид

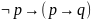
31. Формула, выражающая правило modus ponens, имеет вид

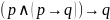
32. Формула, выражающая правило modus tollens, имеет вид

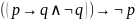
33. Формула, выражающая правило перестановки посылок, имеет вид

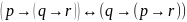
34. Формула, выражающая правило объединения и разделения посылок, имеет вид

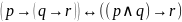
35. Формула, выражающая правило разбора случаев, имеет вид ((q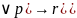

36. Формула, выражающая правило приведения к противоречию, имеет вид

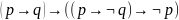
37. Формула, выражающая правило «конъюнкция сильнее каждого из сомножителей», имеет вид

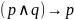
38. Формула, выражающая правило «дизъюнкция слабее каждого из слагаемых», имеет вид

39. Какая из формул выражает один из законов де Моргана

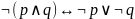
40. Какая из формул выражает один из законов поглощения