
- •Функции алгебры логики
- •16. В каком столбце таблицы находятся значения функции ↔ 4
- •Содержательное исчисление высказываний
- •Формулы алгебры высказываний. Формальное исчисление высказываний
- •50. Каким из ниже перечисленных слов следует заменить символ ▼ в следующем определении.
- •Логика предикатов
- •Формулы логики предикатов
- •Теория алгоритмов.
- •101. Каким из ниже перечисленных слов следует заменить символ ▼ в следующем определении.
- •102. Каким из ниже перечисленных слов следует заменить символ ▼ в следующем определении.
- •103. Каким из ниже перечисленных слов следует заменить символ ▼ в следующем определении.
- •106. Каким из ниже перечисленных слов следует заменить символ ▼ в следующем определении.
Логика предикатов
61. Каким
из ниже перечисленных слов или сочетанием
слов следует заменить символ ▼ в
следующем определении. n-местный
предикат – это определённое на множестве
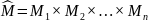 функция, которое при подстановке вместо
элементов
функция, которое при подстановке вместо
элементов
 из множества
из множества
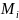 обращается в ▼: высказывание.
обращается в ▼: высказывание.
62.Если при любой подстановке вместо переменных из предикат превращается в истинное высказывание, то он называется тождественно-истинным
63.Если при любой подстановке вместо переменных из предикат превращается в ложное высказывание, то он называется тождественно-ложным.
64.
Предикат
 ,
заданный на множестве
,
называется
выполнимым,
если существует такой набор переменных,
взятый из множеств
,
что при подстановке их вместо
получим истинное
высказывание.
,
заданный на множестве
,
называется
выполнимым,
если существует такой набор переменных,
взятый из множеств
,
что при подстановке их вместо
получим истинное
высказывание.
65. Предикат , заданный на множестве , называется опровержимым, если существует такой набор переменных, взятый из множеств , что при подстановке их вместо получим ложное высказывание.
66. Каким из ниже перечисленных слов или сочетанием слов следует заменить символ ▼: в следующем определении.
Операцией
связывания кванторов общности называется
правило, по которому каждому одноместному
предикату P(x),
определенному на множестве М
сопоставляется высказывание
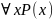 ,
которое истинно тогда и только тогда,
когда P(x)
является ▼ и ложно в противном случае.
тождественно-истинным
предикатом
,
которое истинно тогда и только тогда,
когда P(x)
является ▼ и ложно в противном случае.
тождественно-истинным
предикатом
67 Каким из ниже перечисленных слов или сочетанием слов следует заменить символ ▼ в следующем определении.
Операция
связывания кванторов существования
называется правило, по которому каждому
одноместному предикату P(x),
определенному на множестве М сопоставляется
высказывание
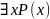 ,
которое ложно в том и только том случае,
когда P(x)
является ▼ и истинно в противном
случае.
тождественно
ложным предикатом
,
которое ложно в том и только том случае,
когда P(x)
является ▼ и истинно в противном
случае.
тождественно
ложным предикатом
68. Каким из ниже перечисленных слов или сочетанием слов следует заменить символ ▼ в следующем определении.
Операцией
связывания кванторов общности по
переменной
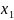 называется
правило, по которому каждому n-местному
предикату
,
определенному на множестве
называется
правило, по которому каждому n-местному
предикату
,
определенному на множестве
 сопоставляется (n-1)-местный
предикат
сопоставляется (n-1)-местный
предикат
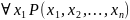 ,
определенный на множестве
,
определенный на множестве
 ,
который на любых наборах
,
который на любых наборах
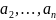 превращается в высказывание
превращается в высказывание
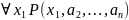 ,
истинное в том и только том случае,
когда одноместный предикат
,
истинное в том и только том случае,
когда одноместный предикат
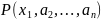 ,
определенный на множестве
,
определенный на множестве
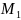 ,
является ▼ и ложно в противном случае.
тождественно-истинным.
,
является ▼ и ложно в противном случае.
тождественно-истинным.
г) тождественно ложным предикатом:
69
Операцией связывания кванторов
существования по переменной
называется
правило, по которому каждому n-местному
предикату
,
определенному на множестве
,
сопоставляется (n-1)-местный
предикат
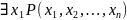 ,
определенный на множестве
,
который на любых наборах
превращается в высказывание
,
определенный на множестве
,
который на любых наборах
превращается в высказывание
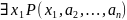 ,
ложное в том и только том случае, когда
одноместный предикат
,,
определенный на множестве
,
является ▼ и истинно в противном случае.
тождественно
ложным предикатом:
,
ложное в том и только том случае, когда
одноместный предикат
,,
определенный на множестве
,
является ▼ и истинно в противном случае.
тождественно
ложным предикатом:
70. В формуле переменная называется связанной.
71. В формуле переменная называется связанной.
72. В
формуле
переменная
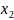 называется свободной.
называется свободной.
73. В формуле переменная называется свободной.
74. Предикат ln(x²+y³)=21,5, где х, у –действительные числа, является выполнимым
75. Предикат x²+y²= -11, где х, у –действительные числа, является тождественно ложным.
76: Предикат ln(x²+y³)=21,5, где х, у –целые числа, является тождественно ложным
77. Предикат x²+y²= -11, где х, у –комплексные числа, является выполнимым
78. Предикат «Формальная теория высказываний является x» где x есть одно из понятий множества {формальная теория, полная теория, разрешимая теория, непротиворечивая теория} является
тождественно истинным.
79. Предикат «Формальная теория предикатов является x» где x есть одно из понятий множества {формальная теория, полная теория, разрешимая теория, непротиворечивая теория} является
выполнимым
80. Формула является открытой
