13. Закон Паскаля и его практическое применение

 На основании основного уравнения гидростатики может быть сформулирован закон Паскаля: внешнее давление, производимое на свободную поверхность покоящейся жидкости, передается одинаково всем ее точкам по всем направлениям.

Свойство жидкости передавать производимое на нее без изменения давления используется в различных гидростатических устройствах: гидравлических прессах, домкратах, гидроаккумуляторах и др.

Гидравлический пресс предназначен для создания больших усилий, необходимых в ряде производственных процессов. На рис. 5 дана схема гидравлического пресса. Принцип его работы следующий. В рабочий цилиндр 2 поршнем 1 насоса подается под давлением рабочая жидкость, например масло. Давление, создаваемое поршнем 1: p=F₁/A₁,

 где       F₁ – сила, действующая на поршень 1;A₁ – площадь его поперечного сечения.

 Рабочая жидкость передает развиваемое поршнем 1 давление поршню 4 рабочего цилиндра 3. Сила, развиваемая поршнем 4: F₂ = pA₂,

 где А₂ –площадь поперечного сечения поршня 4.

 Откуда р = F₂/A₂. Тогда F₂/A₂ = F₁/A₁ или

F2 = F1 × A2/A1 = pA2

 т.е. сила F₂ во столько раз больше силы F₁, во сколько раз площадь поршня 4 больше площади поршня 1.

В действительности сила, развиваемая прессом, несколько меньше силы, определяемой по формуле (17), из-за действия сил трения, возникающих в движущихся частях пресса, а также утечек жидкости. Эти потери учитывают коэффициентом полезного действия (КПД) h пресса, который равен h = 0,75...0,85. Поэтому действительная сила, развиваемая прессом: P = pS_2h.

Гидроаккумулятор предназначен для накопления (аккумулирования) энергии с тем, чтоб отдать ее при необходимости выполнить кратковре­менную работу, требующую больших усилий. Гидроаккумуляторы широ­ко применяют в современных мощных гидравлических прессах, в машинах для литья под давлением при принудительном заполнении расплав­ленным металлом литейных форм, в устройствах привода движения створов гидрошлюзов и т.д. Принцип работы тот же, что и у гидравлического пресса.

На рис. 6 показан грузовой гидроаккумулятор, состоящий из цилиндра 2, внутри которого перемещается плунжер 1. По трубопроводу 4 насосом подается жидкость (обычно масло) в цилиндр. Плунжер вместе с грузами поднимается вверх. После достижения верхней точки насос автоматически выключается.

В положении, при котором груз поднялся на высоту Н, запас потенциальной энергии гидроаккумулятора равен mgH, где m – масса плунжера с грузами. При этом давление внутри цилиндра p=mg/A, где А – площадь поперечного сечения плунжера. Под таким же давлением жидкость подается через трубопровод 3 к исполнительным машинам и механизмам.

 

Рисунок 5 – Гидравлический пресс

15.Вакуумметрическое давление

Вакуумом называется разность между атмосферным давлением и давлением в разреженном пространстве, то есть величина вакуума пока­зывает, на сколько давление в сосуде меньше атмосферного.

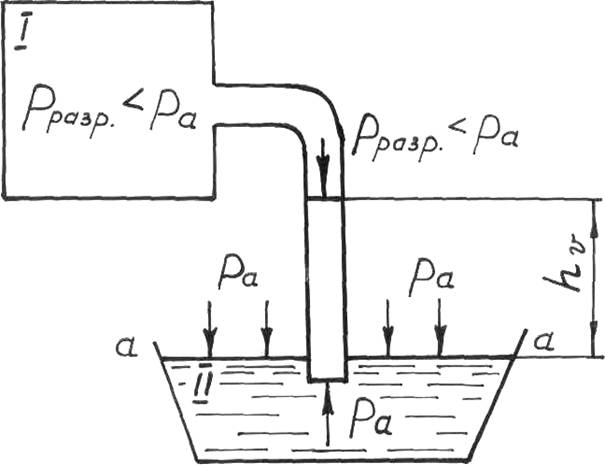
Рисунок 3 – Схема, поясняющая понятие вакуума.

Рассмотрим два сосуда, соединенных между собой. Сосуд II заполнен жидкостью и имеет давление на свободной поверхности, равное атмосферному р_а. В сосуде I, откачивая воздух, создадим разрежение с давлением р_разр. меньше атмосферного. Тогда жидкость из сосуда II начнет подниматься по трубке. Пусть при каком-то р_разр. уровень в трубке поднялся на высоту h_v. Рассмотрим равновесие частиц жидкости в трубке на уровне а-а. Так как они находятся в равновесии, то это значит, что давление со стороны сосуда I, равное P_разр + g × h_v, и давление со стороны сосуда II, равное р_а, одинаковы. Тогда p_разр.+ g × h_v = p_a, отсюда

ра – рразр = g × hv = pv

 где р_v – вакуумметрическое давление или вакуум. Теоретические пределы вакуума:0- когда р_а = р_разр. 1 aт - когда р_разр = 0.

 Практически вакуум не достигает 1 aт, так как в действительности величина разрежения не будет совершенной пустотой: при сильном раз­режении пространство частично заполняется парами самой жидкости и выделяемым из жидкости растворенным в ней воздухом.

18. Расход и средняя скорость потока

Расходом называется количество жидкости, протекающей через жи­вое сечение потока в единицу времени. Различают объемный Q, массовый М и весовой G расходы жидкостей:

;
;

 где       Q – объем жидкости; m – масса жидкости; t – время.

 Между этими расходами существует зависимость

.

 Для элементарной струйки, имеющей бесконечно малую площадь поперечного сечения и одинаковую истинную скорость v во всех точках каждого сечения, элементарный расход составляет dQ = n × dA. Таким обра­зом, объемный расход элементарной струйки равен произведению площа­ди ее живого сечения на скорость в этом сечении.

Объемный расход потока равен сумме элементарных расходов струек:

.

 

Скорость жидкости в различных точках живого сечения различна, и точный закон изменения скорости по сечению не всегда известен, поэтому вычисление интеграла(5б)в ряде случаев затруднительно. Для упрощения расчетов вводят понятие средней для данного живого сечения скорости потока n_ср = Q/A, откуда

Q = VcрA

 Средняя скорость – это фиктивная скорость потока, которая счита­ется одинаковой для всех частиц данного сечения, но подобрана так, что расход, определенный по ее значению, равен истинному значению расхо­да.

Установившееся движение жидкости, характеризующееся постоян­ством расхода во времени, подразделяют на равномерное и неравномер­ное.

Равномерным называется такое установившееся движение жидко­сти, при котором скорость и площади живых сечений потока не изменя­ются по его длине. Примером равномерного движения может служить ус­тановившееся движение жидкости в цилиндрической трубе.

Неравномерным называется такое установившееся движение, при котором средняя скорость и площади живых сечений потока изменяются по его длине. Примером служит установившееся движение жидкости в трубе переменного сечения.

При изучении неравномерного движения жидкости пользуются понятием плавноизменяющегося движения, при котором: 1) радиус кривизны линий тока очень велик и в пределе стремится к бесконечности; 2) угол расхождения между линиями тока очень мал и в пределе стремится к нулю; 3) живые сечения струек — плоские площадки, нормальные к оси потока. Следовательно, плавноизменяющееся движение по своим свойствам приближается к равномерному движению, состоящему из прямых и параллельных между собой элементарных струек.