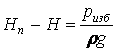Гидравликой называют науку, изучающую законы равновесия и движения различных жидкостей и методы применения этих законов для решения практических задач.Название «гидравлика» происходит от сочетания греческих слов «хюдор» - вода и «аулос» - труба, желоб, и первоначально обозначало учение о движении воды по трубам. Такая трактовка гидравлики имеет теперь лишь историческое значение, т.к. с развитием производства и техники область применения законов гидравлики существенно расширилась.На законах гидравлики основан расчет разнообразных гидротехнических сооружений (например: плотин, каналов, водосливов), трубопроводов для подачи различных жидкостей, гидромашин (насосов, гидротурбин, гидропередач), а также других гидравлических устройств, применяемых во многих областях техники.Основные разделы гидравлики:1.  гидростатика, изучающая законы покоя (равновесия) жидкостей;2.  гидродинамика, изучающая законы движения жидкостей.

1. Физические свойства жидкости

Жидкость — непрерывная среда, обладающая свойством текучести, т. е. способная неограниченно изменять свою форму под действием сколь угодно малых cил, но в отличие от газа мало изменяющая свою плотность при изменении давления.

В аэромеханике применяют термин «капельная жидкость» с целью под­черкнуть отличие жидкости от газа; газ в этих случаях называют «сжимае­мой жидкостью».

Жидкости бывают идеальные и реальные. Идеальные - невязкие жидкости, обладающие абсолютной подвижностью, т.е. отсутствием сил трения и касательных напряжений и абсолютной неизменностью, а объёме под воздействием внешних сил. Реальные - вязкие жидкости, обладающие сжимаемостью, сопротивлением, растягивающим и сдвигающим усилиям и достаточной подвижностью, т.е. наличием сил трения и касательных напряжений.

Реальные жидкости могут быть ньютоновскими и неньютоновскими (бингамовскими). В ньютоновских жидкостях при движении одного слоя жидкости относительно другого величина касательного напряжения пропорциональна скорости сдвига. При относительном покое эти напряжения равны нулю. Такая закономерность была установлена Ньютоном в 1686 году, поэтому эти жидкости (вода, масло, бензин, керосин, глицерин и др.) называют ньютоновскими жидкостями. Неньютоновские жидкости не обладают большой подвижностью и отличаются от ньютоновских жидкостей наличием касательных напряжений (внутреннего трения) в состоянии покоя.

Основные свойства жидкостей: плотность, удельный вес, вязкость, сжимаемость и др.

Плотность ρ - масса жидкости в единице объема. Для однородной жидкости

ρ=m/V

где  m - масса жидкости в объеме V. Единицы измерения ρ в системе СГС - г/см³, в системе МКГСС - кгс·с²/м⁴, а в системе СИ - кг/м³.

Удельный вес γ - вес жидкости в единице объема:

γ=G/V

где G - вес жидкости. Единицы измерения γ в системе СГС - дин/см³, в системе МКГСС - кгс/м³, а в системе СИ - Н/м³.

Удельный вес и плотность связаны между собой зависимостью γ=ρ·g, где g - ускорение свободного падения.

Сжимаемость - свойство жидкости изменять свой объем под действием давления. Сжимаемость жидкостей характеризуется коэффициентом объемного сжатия β_р, который выражает относительное изменение объема жидкости V₀, отнесенное к единице давления p и определяется по формуле

β_р=(-dV/V₀)·(1/dp),

Знак минус в формуле обусловлен тем, что положительному прира­щению давления соответствует отрицательное приращение (уменьшение) объема. Единицы измерения β_р в системе МКГСС — м²/кгс, в системе СИ -  1/Па. Часто β_р выражается в см²/кгс.

Вязкость - свойство жидкости оказывать сопротивление относительному движению (сдвигу) частиц жидкости. Это свойство обусловлено возникновением в движущейся жидкости сил внутреннего трения, ибо они проявляются только при ее движении благодаря наличию сил сцепления между ее молекулами. Характеристиками вязкости являются: динамический коэффициент вязкости μ и кинематический коэффициент вязкости ν.

Единицей динамического коэффициента вязкости в системе СГС является пуаз (П): 1 П=1 дина·с/см²=1 г/(см·с). Сотая доля пуаза носит название сантипуаз  (сП): 1  сП=0,01П. В системе МКГСС единицей динамического коэффициента вязкости является кгс·с/м²; в системе СИ - Па·с. Связь между единицами следующая: 1 П=0,010193 кгс·с/м²=0,1 Па·с; 1 кгс·с/м²=98,1 П=9,81 Па·с.

Кинематический коэффициент вязкости

ν=μ/ρ,

Единицей кинематического коэффициента вязкости в системе СГС является стокc (Ст), или 1 см²/с, а также сантистокс (сСт): 1 сСт=0,01 Ст. В системах МКГСС и СИ единицей кинематического коэффициента вязкости является м²/с:  1 м²/с=10⁴Ст.

Вязкость жидкости с повышением температуры уменьшается. Влияние температуры на динамический коэффициент вязкости жидкостей оценивается формулой μ = μ₀·e^­a(t-t₀⁾, где μ = μ₀ - значения динамического коэффициента вязкости соответственно при температуре t и t₀ градусов; а - показатель степени, зависящий от рода жидкости; для масел, например, значения его изменяются в пределах 0,025—0,035.

2.3.4.5.Гидростатическое давление его свойства

Рассмотрим некоторый объем жидкости, находящейся в покое (рис. 1). Разделим его произвольной плоскостью А–В на две части. Верхняя часть жидкости I давит на нижнюю II по плоскости раздела с силой F. Для нижней части сила F является внешней поверхностной силой. Сила F, действующая на всю площадку А, называется суммарной силой гидростатического давления. Отношение нормальной силы F к площади А, на которую она действует, называется средним гидростатическим давлением: 

 Единицей гидростатического давления является 1 Н/м². Эта единица называется Паскаль (1 Па = 1 Н/м ).

Эта единица давления неудобна для практического использования ввиду ее малости. Поэтому удобнее давление измерять в барах (1бар=0,987 aт). По своей величине эта единица близка к 1 aт (1бар=0,987 aт).

Давление на практике часто измеряют в физических и технических атмосферах.

Физической атмосферой называют среднее давление атмосферного воздуха на уровне моря при температуре 0° С и обозначают сокращенно атм:

1 атм = 1,01325×10⁵ н/м².

 Это давление может быть уравновешено столбиком ртути высотой 760 мм или столбом воды высотой 10330 мм.

В технике и технических расчетах пользуются технической атмосферой, которую обозначают aт:

 1 ат = 0,980665 × 10⁵н/м².

Давление 1 aт может быть уравновешено столбиком ртути высотой 735,5 мм или столбом воды высотой 10000 мм:

 1 мм рт.ст. = 133,322 н/м²; 1 мм вод.ст. = 9,80665 н/м².

Атмосферное давление, измеряемое барометром, называют барометрическим и обозначают р_бар.

Многие процессы протекают при давлениях выше атмосферного (давление пара в котле, давление, созданное столбом жидкости, и т.п.). Любое из этих давлений является дополнительным к атмосферному, т.е. избыточным. Избыточное давление измеряют манометром и обозначают р_изб или р_ман.

Сумму давлений манометрического и барометрического называют полным, или абсолютным, давлением:

рабс= рман +рбар

 Если процессы протекают при разрежении (вакууме), то абсолютным (полным) давлением называют разность барометрического давления и разрежения: 

рабс=рбар-рвак

 где       р_вак – разрежение, измеренное вакуумметром.

 Если уменьшать площадь А до нуля, то среднее гидростатическое давление будет стремиться к определенному пределу, который называют гидростатическим давление в точке, Па:

 Гидростатическое давление обладает тремя следующими свойствами:

1.   гидростатическое давление всегда действует нормально к площадке и является сжимающим, т.е. оно направлено по нормали внутрь рассматриваемого объема жидкости;

2.   гидростатическое давление р в любой точке внутри жидкости по всем направлениям одинаково, т.е. не зависит от угла наклона площадки, на которую оно действует;

3.   Гидростатическое давление в точке зависит от ее координат в пространстве, т.е. p = f (x,y,z).

 

 

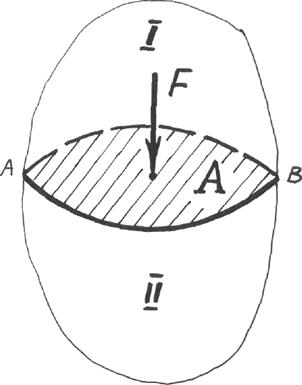
Рисунок 1 – Схема, поясняющая понятие гидростатического давления.

 

 

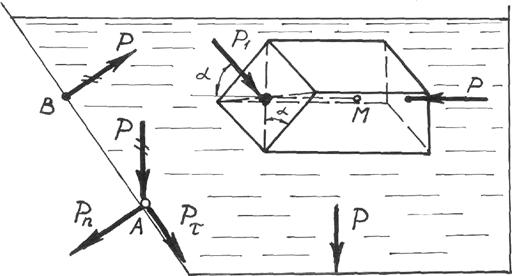
Рисунок 2 – Схема к рассмотрению свойств гидростатического давления.

7.Основное уравнение гидростатики

 

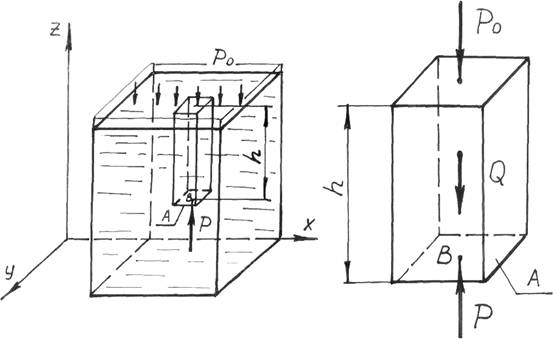
Рисунок 4 – Схема к выводу основного уравнения гидростатики.

 

Имеем сосуд с жидкостью, которая находится в покое. Давление на свободной поверхности равно р₀. Требуется определить величину гидро­статического давления в точке В, расположенной на глубине h от свобод­ной поверхности. Выделим вокруг точки В площадку А, а затем верти­кальную призму с основанием А и высотой h. Рассмотрим равновесие этой призмы. На неё действуют силы:

1.   сверху вниз сила давления на площадь А, равная Р₀×А и сила тяжести рассматриваемого объема Q = ghA, где g – удельный вес жидкости, н/м³; hA –объем жидкости, находящейся в призме, м³;

2.   снизу вверх сила гидростатического давления на нижнюю площадку А, равная рА, где р-гидростатическое давление в точке В на глубине h.

Так как рассматриваемый объем находится в равновесии, то сумма проекций всех сил на ось Z должна равняться нулю, то есть

 Силы, действующие на боковые поверхности, горизонтальны и про­екций на вертикальную ось не дают.

При сокращении на А и переносе членов уравнения равновесия из одной части уравнения в другую, получим:

p=po+gh - основное уравнение гидростатики

 где       р – абсолютное давление в точке, Па; р₀ – внешнее давление (в частном случае атмосферное), Па; gh – избыточное давление (манометрическое), Па.

Гидростатическое давление в любой точке покоящейся жидкости равно давлению на свободной поверхности, сложенному с произведением удельного веса жидкости на глубину погружения этой точки от свободной поверхности.

9. Давление жидкости на плоскую наклонную стенку

Пусть мы имеем резервуар с наклонной правой стенкой, заполненный жидкостью с удельным весом γ. Ширина стенки в направлении, перпендикулярном плоскости чертежа (от читателя), равна b (рис.2.3). Стенка условно показана развернутой относительно оси АВ и заштрихована на рисунке. Построим график изменения избыточного гидростатического давления на стенку АВ.

Так как избыточное гидростатическое давление изменяется по линейному закон P=γgh, то для построения графика, называемого эпюрой давления, достаточно найти давление в двух точках, например А и B.

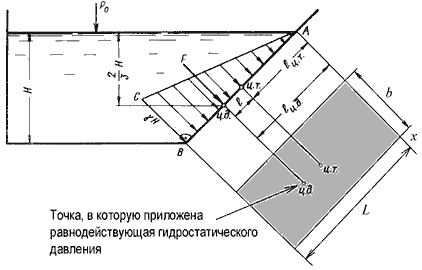
Рис. 2.3. Схема к определению равнодействующей гидростатического давления на плоскую поверхность

Избыточное гидростатическое давление в точке А будет равно

P_A = γh = γ·0 = 0

Соответственно давление в точке В:

P_B = γh = γH

где H - глубина жидкости в резервуаре.

Согласно первому свойству гидростатического давления, оно всегда направлено по нормали к ограждающей поверхности. Следовательно, гидростатическое давление в точке В, величина которого равна γH, надо направлять перпендикулярно к стенке АВ. Соединив точку А с концом отрезка γH, получим треугольную эпюру распределения давления АВС с прямым углом в точке В. Среднее значение давления будет равно

Если площадь наклонной стенки S=bL, то равнодействующая гидростатического давления равна

где hc = Н/2 - глубина погружения центра тяжести плоской поверхности под уровень жидкости.

Однако точка приложения равнодействующей гидростатического давления ц.д. не всегда будет совпадать с центром тяжести плоской поверхности. Эта точка находится на расстоянии l от центра тяжести и равна отношению момента инерции площадки относительно центральной оси к статическому моменту этой же площадки.

где J_Аx - момент инерции площади S относительно центральной оси, параллельной Аx.

В частном случае, когда стенка имеет форму прямоугольника размерами bL и одна из его сторон лежит на свободной поверхности с атмосферным давлением, центр давления ц.д. находится на расстоянии b/3 от нижней стороны.

10.Давление жидкости на цилиндрическую поверхность

Пусть жидкость заполняет резервуар, правая стенка которого представляет собой цилиндрическую криволинейную поверхность АВС (рис.2.4), простирающуюся в направлении читателя на ширину b. Восстановим из точки А перпендикуляр АО к свободной поверхности жидкости. Объем жидкости в отсеке АОСВ находится в равновесии. Это значит, что силы, действующие на поверхности выделенного объема V, и силы веса взаимно уравновешиваются.

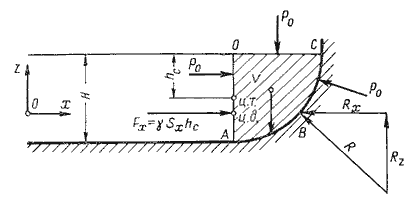
Рис. 2.4. Схема к определению равнодействующей гидростатического давления на цилиндрическую поверхность

Представим, что выделенный объем V представляет собой твердое тело того же удельного веса, что и жидкость (этот объем на рис.2.4 заштрихован). Левая поверхность этого объема (на чертеже вертикальная стенка АО) имеет площадь Sx = bH, являющуюся проекцией криволинейной поверхности АВС на плоскость yOz.

Cила гидростатического давления на площадь S_x равна F_x = γ S_xh_c.

С правой стороны на отсек будет действовать реакция R цилиндрической поверхности. Пусть точка приложения и направление этой реакции будут таковы, как показано на рис.2.4. Реакцию R разложим на две составляющие R_x и R_z.

Из действующих поверхностных сил осталось учесть только давление на свободной поверхности Р₀. Если резервуар открыт, то естественно, что давление Р₀ одинаково со всех сторон и поэтому взаимно уравновешивается.

На отсек АВСО будет действовать сила собственного веса G = γV, направленная вниз.

Спроецируем все силы на ось Ох:

F_x - R_x = 0 откуда F_x = R_x = γS_xh_c

Теперь спроецируем все силы на ось Оz:

R_x - G = 0 откуда R_x = G = γV

Составляющая силы гидростатического давления по оси O_y обращается в нуль, значит R_y = F_y = 0.

Таким образом, реакция цилиндрической поверхности в общем случае равна

а поскольку реакция цилиндрической поверхности равна равнодействующей гидростатического давления R=F, то делаем вывод, что

11.Приборы для измерения давления

  Рисунок 9 – Пьезометр.

Давление измеряют жидкостными и пружинными манометрами, а также пьезометрами.

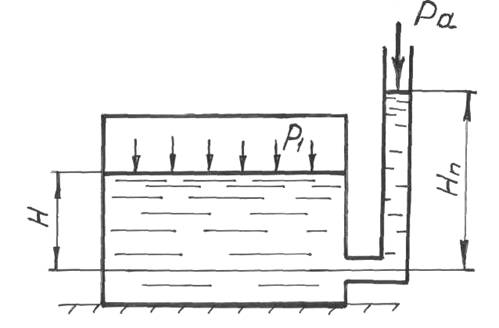
Пьезометром измеряют давление жидкости высотой столба той же жидкости. Он представляет собой открытую сверху трубку, присоединенную нижним концом к месту измерения давления (рис. 9). Жидкость в пьезометре поднимается (если давление в месте измерения больше атмосферного) на высоту Н_п, называемую пьезометрической высотой. При этом давление в точке измерения складывается из давления pi на свобод­ную поверхность жидкости, заключенной в сосуд, и давления столба жид­кости высотой Н. Оно уравновешивается давлением в пьезометре p_a + pgH_n:  pgH = p_a + pgH_n.

Откуда 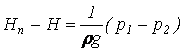      или

 

 Таким образом, чем больше разность давления на свободную поверхность жидкости, заключенной в сосуд, и атмосферного давления, тем больше разность высот уровней жидкости в пьезометре и в сосуде.

Пьезометрами измеряют давление жидкости, в частности воды, незначительно отличающееся от атмосферного, так как большие и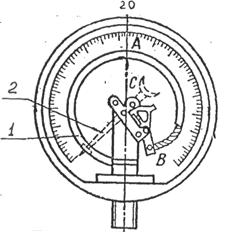 збыточные давления могут быть уравновешены лишь давлением столба воды большой высоты.

 

 

 

 

Рисунок 10 – Пружинный манометр: 1-трубка; 2-стрелка.

Пружинными манометрами измеряют значительные давления жидкостей и газов. Схема такого манометра показана на рис. 10. Он состоит из спиральной трубки 1, один конец которой запаян, а другой, открытый, конец сообщается с. сосудом, в котором измеряют давление. Рабочее тело оказывает давление р на внутреннюю поверхность трубки. На внешнюю ее поверхность действует давление р_а наружного воздуха. Под действием разности давлений р – р_а = р_ман трубка раскручивается (выпрямляется) тем сильнее, чем больше эта разность. К запаянному концу трубки прикреплен механизм, поворачивающий на соответствующий угол указательную стрелку 2.

Таким образом, с помощью манометра измеряют не абсолютное давление в сосуде, а избыточное давление в нем. Абсолютное давление в сосуде.

рабс = рман + ра

 где      р_ман – давление, которое показывает манометр.

 Вакуумметры применяют для измерения вакуума. Абсолютное дав­ление среды, измеренное вакуумметром:

рабс = ра – рвак

 

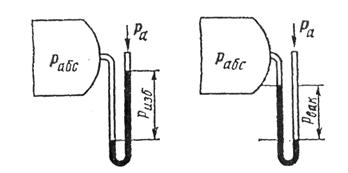
Рисунок 11 – Жидкостный U - образный манометр.

Жидкостные U-образные манометры (рис. 11) применяют для измерения малых давлений. Измеряемое давление зависит от плотности применяемой в манометре жидкости, поэтому при пользовании жидкостными манометрами следует оговаривать, какая жидкость употребляется. Наиболее часто в жидкостных манометрах используют ртуть, воду или спирт.

 

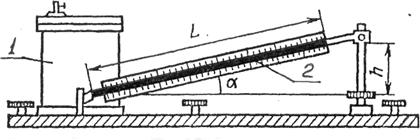
Рисунок 12 – Микроманометр: 1-резервуар; 2-наклонная трубка

Для измерения малых давлений с высокой точностью применяют микроманометры (рис. 12.). Такой микроманометр состоит из резервуара 1 и наклонной трубки 2 со шкалой. В резервуар налита жидкость (чаще всего спирт), а один конец трубки входит в резервуар, образуя с ним сообщающиеся сосуды. При давлении p = p₁ – р₂ на жидкость в сосуде, она перемещается в трубке и занимает на шкале положение L. При угле a наклона трубки, давление, измеряемое микроманометром, определяют по формуле р = pgL × sina.

Прибор монтируют в корпусе, устанавливаемом с помощью регули­ровочных винтов строго по уровню.

Для измерения разности давлений в двух резервуарах или в двух точках одного трубопровода часто применяют так называемые дифференциаль­ные манометры. Схема присоединения такого манометра к измеряемму объекту показана на рис. 13.

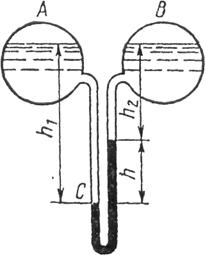  Рисунок 13 – Дифференциальный манометр.

Пусть на поверхности жидкости плотностью r в сосуде А давление р_А, на поверхности жидкости с той же плотностью r в сосуде В - давление р_в. Если манометр заполнен жидкостью, плотность которой р_ман, то можно записать следующее равенство:

рА = rgh1 = pB + rgh2 + rманgh2

 Учитывая, что h₂ – h₁ = – h, получим

рА – pB = (rман – r)gh

 Таким образом, разность давлений определяется разностью уровней жидкостей в коленах дифференциального манометра и разностью плотно­стей жидкостей в манометре и измеряемых резервуарах.