9) Взаимное положение плоскостей. Параллельность плоскостей.

Две произвольные плоскости в пространстве по отношению друг к другу могут занимать два положения:

плоскости пересекаются, при этом линия их пересечения всегда прямая;

плоскости параллельны друг другу.

Условия пересечения плоскостей

Две произвольные плоскости в пространстве пересекаются по прямой линии. Как известно, две точки вполне определяют единственную прямую в пространстве. Следовательно, задача по построению линии пересечения плоскостей сводится к определению положения двух принадлежащих им обеим точек. Прямая пересечения плоскостей может быть построена и при условии, если определена одна общая для плоскостей точка и известно направление этой линии.

Условия параллельности плоскостей

Две плоскости параллельны, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости:

если плоскости заданы пересекающимися прямыми, то они будут параллельны в случае, когда одноименные проекции прямых, лежащих в разных плоскостях, будут параллельны;

если плоскости заданы линиями уровня (фронталями и горизонталями), то они будут параллельны в случае, когда одноименные проекции линий уровня параллельны между собой;

если плоскости заданы следами, то они параллельны тогда, когда параллельны их одноименные следы;

если плоскости заданы любым другим способом, то в них необходимо построить пересекающиеся прямые (общего положения, уровня или следы) и сравнить одноименные их проекции. У параллельных плоскостей одноименные проекции пересекающихся прямых взаимно параллельны.

В техническом рисовании аксонометрические изображения начинают с нанесения аксонометрических осей, выполняя все операции от руки на глаз, без применения чертежных инструментов. Аксонометрические рисунки правильных треугольников и шестиугольников показаны на рис.. Длины соответствующих отрезков с ортогонального изображения многоугольника переносятся на аксонометрические оси.

10) Пересечение плоскостей частного положения.

Плоскости частного положения - это плоскости перпендикулярные или параллельные какой-либо плоскости проекций.

Плоскости перпендикулярные одной из плоскостей проекций, называются проецирующими.

1. Горизонтально проецирующая плоскость перпендикулярна горизонтальной плоскости проекций 1 (рис. 4.3а).

 

Рис. 4.3а. Горизонтально проецирующая плоскость.

Фронтальный след 1 перпендикулярен оси x. Профильный след 3 перпендикулярен оси y.

 - угол наклона плоскости  к плоскости 2.  - угол наклона плоскости  к плоскости 3. Горизонтальная проекция всех точек плоскости  совпадает с её горизонтальными следами.

2. Фронтально проецирующая плоскость перпендикулярна фронтальной плоскости проекций 2 (рис. 4.3б) горизонтальный след 1 - перпендикулярен оси x, профильный след 3 перпендикулярен оси z,  - угол наклона плоскости  к плоскости 1.  - угол наклона плоскости  к плоскости 3. Фронтальные проекция всех точек плоскости  совпадают с ее фронтальным следом.

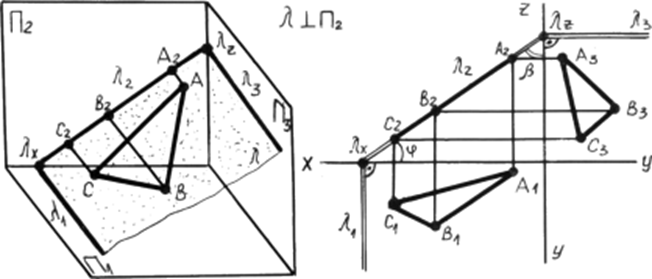
Рис. 4.3б. Фронтально проецирующая плоскость.

 

3. Профильно-проецирующая плоскость перпендикулярна

профильной

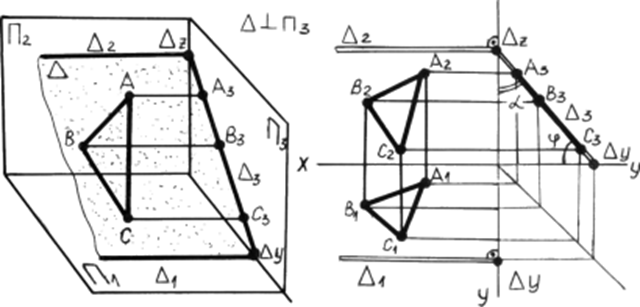
Рис. 4.3в. Профильно проецирующая плоскость.

Горизонтальный след 1 перпендикулярен оси y, фронтальный след 2 перпендикулярен оси z.

 - угол наклона плоскости  к плоскости 1. - угол наклона плоскости  к плоскости 2. Профильные проекции всех точек плоскости  совпадают с ее профильным следом.

Плоскости параллельные какой-либо из плоскостей проекций и перпендикулярные двум другим называются плоскостями уровня.

1. Горизонтальные плоскость уровня параллельна плоскости 1

Рис. 4.4а. Горизонтальные плоскость уровня.

Фронтальная и профильная проекции плоскости совпадают с ее следами 1 и 2, которые перпендикулярны оси z. На горизонтальную плоскость 1 любая фигура, расположенная в плоскости , проецируется без искажения на 1.

2. Фронтальная плоскость уровня параллельна плоскости 2 и перпендикулярна плоскостям 1 и 3 (рис. 4.4б).

Горизонтальная и профильная проекции плоскости совпадают с её следами 1 и 3, которые перпендикулярны оси y. На фронтальную плоскость

2 любая фигура, расположенная в плоскости , проецируется без искажения.

Рис. 4.4б. Фронтальная плоскость уровня.

3. Профильная плоскость уровня параллельна плоскости 3 и перпендикулярна плоскостям 2 и 3 (рис. 4.4в).

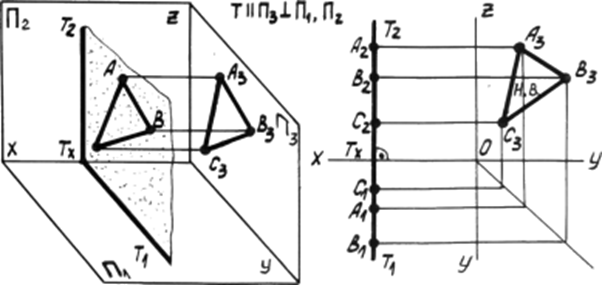
Рис. 4.4в. Профильная плоскость уровня.

Фронтальная и горизонтальная проекции плоскости совпадают с её следами Т1 и Т2, которые перпендикулярны оси x. На профильную плоскость 3 любая фигура, расположенная в плоскости Т, проецируется без искажения.

Свойства плоскостей частного положения:

1. Любая геометрическая фигура расположенная в плоскости, перпендикулярной какой-либо плоскости проекций, проецируется на соответствующий след этой плоскости.

2. Любая геометрическая фигура расположенная в плоскости уровня, проецируется без искажения на ту плоскость проекций, которой данная плоскость параллельна.