
- •6. Работа, мощность, энергия
- •7. Кинетическая и потенциальная энергия
- •Формы записи закона сохранения энергии в классической физике
- •Расширенная форма записи закона сохранения энергии
- •9. Закон сохранения импульса.
- •11. Удар абсолютно упругих и неупругих тел
- •12. Момент импульса
- •14. Момент инерции
- •14.1 Теорема Штейнера
- •15. Кинетическая энергия вращения
- •16. Момент импульса. Тензор инерции.
- •17. Свободные оси. Гироскоп
- •18. Деформация твердого тела
- •19. Неинерциальные системы отсчета и силы инерции
14. Момент инерции
Моментом
инерции системы
(тела) относительно данной оси называется
физическая величина, равная сумме
произведений масс n материальных точек
системы на квадраты их расстояний до
рассматриваемой оси: 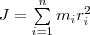 В
случае непрерывного распределения
масс эта сумма сводится к интегралу
В
случае непрерывного распределения
масс эта сумма сводится к интегралу ![]() где
интегрирование производится по всему
объему тела. При этом величина r в есть
функция положения точки с координатами
х, у, z. В качестве примера будем искать
момент инерции однородного сплошного
цилиндра высотой h и радиусом R относительно
его геометрической оси (рис. 1).
где
интегрирование производится по всему
объему тела. При этом величина r в есть
функция положения точки с координатами
х, у, z. В качестве примера будем искать
момент инерции однородного сплошного
цилиндра высотой h и радиусом R относительно
его геометрической оси (рис. 1).
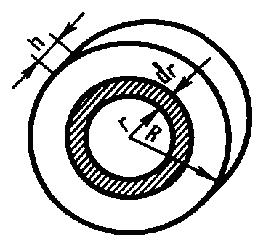
Рис.1
Разобьем
цилиндр на отдельные полые концентрические
цилиндры бесконечно малой толщины dr с
внутренним радиусом r и внешним r+dr.
Момент инерции отдельного полого
цилиндра dJ=r2dm
(так как dr<<r, то считаем, что расстояние
всех точек цилиндра от оси равно r), где
dm - масса всего элементарного цилиндра;
его объем 2πrhdr. Если ρ-плотность материала,
то dm=2πrhρdr и dJ=2πhρr3dr.
Тогда момент инерции сплошного
цилиндра 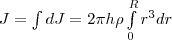 но
так как πR2h - объем цилиндра, то его масса
m=πR2hρ, а момент инерции
но
так как πR2h - объем цилиндра, то его масса
m=πR2hρ, а момент инерции ![]() Если
мы знаем момент инерции тела относительно
оси, проходящей через его центр масс,
то мы можем найти и момент инерции
относительно любой другой параллельной
этой оси, который можно найти с
помощью теоремы
Гюйгенса-Штейнера: момент
инерции тела J относительно произвольной
оси равен моменту его инерции
Jc относительно
параллельной оси, проходящей через
центр масс С тела, сложенному с
произведением массы m тела на квадрат
расстояния а между осями:
Если
мы знаем момент инерции тела относительно
оси, проходящей через его центр масс,
то мы можем найти и момент инерции
относительно любой другой параллельной
этой оси, который можно найти с
помощью теоремы
Гюйгенса-Штейнера: момент
инерции тела J относительно произвольной
оси равен моменту его инерции
Jc относительно
параллельной оси, проходящей через
центр масс С тела, сложенному с
произведением массы m тела на квадрат
расстояния а между осями: ![]() Приведем
значения моментов инерции (табл. 1) для
некоторых тел (тела считаются однородными,
m - масса тела).
Приведем
значения моментов инерции (табл. 1) для
некоторых тел (тела считаются однородными,
m - масса тела).

14.1 Теорема Штейнера
Материал из Википедии — свободной энциклопедии
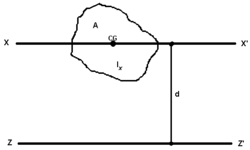
Иллюстрация теоремы для момента площади.
У этого термина существуют и другие значения, см. Теорема Штейнера (значения).
Теоре́ма
Гю́йгенса — Ште́йнера,
или просто теорема
Штейнера (названа
по имени швейцарского математика Якоба
Штейнераи
голландского математика, физика и
астронома Христиана
Гюйгенса): момент
инерции тела J относительно
произвольной оси равен сумме момента
инерции этого тела JC относительно
параллельной ей оси, проходящей через
центр масс тела, и произведения массы
тела m на
квадрат расстояния d между
осями:
![]() где
JC —
известный момент инерции относительно
оси, проходящей через центр масс тела,J —
искомый момент инерции относительно
параллельной оси,m —
масса тела,d —
расстояние между указанными осями.
где
JC —
известный момент инерции относительно
оси, проходящей через центр масс тела,J —
искомый момент инерции относительно
параллельной оси,m —
масса тела,d —
расстояние между указанными осями.
Момент инерции,
по определению:
![]() Радиус-вектор
Радиус-вектор ![]() можно
расписать как разность двух векторов:
можно
расписать как разность двух векторов:
![]() ,где
,где ![]() —
радиус-вектор расстояния между старой
и новой осью вращения. Тогда выражение
для момента инерции примет вид:
—
радиус-вектор расстояния между старой
и новой осью вращения. Тогда выражение
для момента инерции примет вид:
![]()
Вынося за сумму , получим:
![]()
Поскольку старая ось проходит через центр масс, то суммарный импульс тела будет равен нулю:
![]()
Тогда:
![]()
Откуда и следует искомая формула:
,
где JC — известный момент инерции относительно оси, проходящей через центр масс тела.
