6.2. Коды Хэмминга и м-последовательности

Коды Хэмминга , где , задаются проверочной матрицей из ненулевых двоичных векторов. Здесь - число проверочных символов в каждом кодовом слове, . Так как , число разных ненулевых синдромов равно числу символов в кодовом слове (см. п. 6.3). Это - класс совершенных кодов с кодовым расстоянием при любых , исправляющих все однократные ошибки и ничего более. Они гарантированно обнаруживают ошибки кратности . Число кодовых слов веса (спектр кода Хэмминга длины ) равно коэффициенту при в полиноме . Если к кодам Хэмминга добавить еще один проверочный символ (путем общей проверки на четность), то получим коды . У них , а спектр задан полиномом .

-последовательности - это коды с параметрами , ., дуальные кодам Хэмминга той же длины, Их составляет множество выходных последовательностей с периодом при разных начальных заполнениях линейного регистра длины со связями, обеспечивающими этот период. Отсюда следует название кодов - последовательности максимальной длины или -последовательности. Все слова этого кода, кроме , имеют одинаковый вес , так что для него . Коды Хэмминга и -последовательности – крайние случаи кодов с малым и большим кодовым расстоянием, соответственно. Они не всегда удобны: исправление лишь однократных ошибок может не обеспечить требуемую верность передачи, а высокая исправляющая способность -последовательностей связана с их низкой кодовой скоростью .

6.3. Коды Адамара

Фазовая манипуляция несущего колебания по закону кодовых слов ортогонального кода Адамара образует ортогональные сигналы . Строки матрицы Адамара образуют кодовые слова. Это - матрица размерности ( - четное) из и . Один ее столбец отличен от другого в позициях. Один столбец состоит из одних , остальные имеют одинаковое число и . При

(6.9)

Из матрицы Адамара можно построить матрицу Адамара :

(6.10)

где - дополнение матрицы (все нули заменяют единицами и наоборот). Применяя (6.10), можно построить линейные коды Адамара длины (целое ), с кодовым расстоянием и . Для существуют нелинейные коды Адамара.

Пример 6.3.1. Подставив (6.9) в (6.10), имеем:

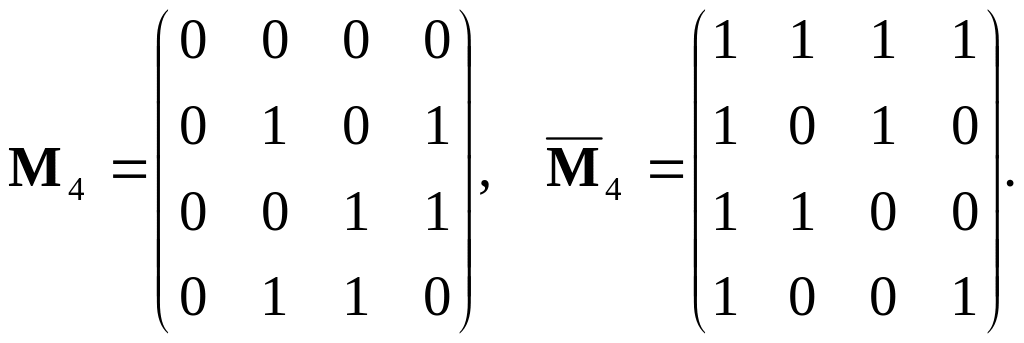
Строки матриц и формируют линейный код длины с объемом алфавита и кодовым расстоянием .

6.4. Полиномиальные коды

Сообщение источника закодируем простым двоичным кодом длины . Символы , , каждого кодового слова служат коэффициентами в информационном полиноме формальной переменной . Каждое кодовое слово полиномиального кода представим полиномом . Порождающий полином полиномиального кода запишем как . Операции сложения, умножения и деления над изучаемыми полиномами выполняются по обычным правилам с учетом суммирования по (см. п. 1.1). Полиномиальный код - множество кодовых слов, полиномы которых образуются по правилу:

(6.11)

Остаток от деления полинома принятого слова, возможно, искаженного ошибками при передаче, на - синдромный полином . Если , принятое слово принадлежит коду (см. (6.11)). Тогда считают, что ошибок при передаче нет. Коэффициенты полинома образуют вектор синдрома. Поиск ошибок сводится к вычислению синдрома.