19. Неравнозначность, таблица истинности и диаграмма Венна.
Неравнозначность (исключающее ИЛИ, сумма по модулю 2) F = X Y
X |
Y |
F |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
20. Конъюнкция, таблица истинности и диаграмма Венна.
Логическая операция КОНЪЮНКЦИЯ (логическое умножение): в естественном языке соответствует союзу и; в алгебре высказываний обозначение &;
Конъюнкция - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
Таблица истинности |
Диаграмма Эйлера- Венна |
|||||||||||||||
|
|
21. Равнозначность. Таблица истинности и диаграмма Венна.
Равнозначность – операция, которая истинна в том случае, когда значение истины обоих аргументов совпадают, в остальном ложно.
A |
B |
F = A B |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
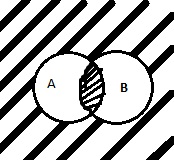
22. Импликация. Таблица истинности и диаграмма Венна.
Импликация - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.
А – антецедент. В – консеквент.
A |
B |
F = A→B |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
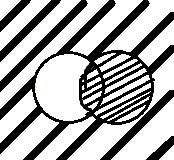
23. Перевод чисел из десятичной СС в двоичную.
Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
24. Перевод чисел из десятичной СС в восьмеричную.
Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
25. Перевод чисел из десятичной СС в шестнадцатеричную.
Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
31. Работа с таблицами в редакторе WORD
Любая таблица состоит из строк и столбцов. Их пересечение образуют ячейки таблицы. Для вставки таблицы служит кнопка "Таблицы", расположенная на панели "Таблицы" лента "Вставка". При нажатии на эту кнопку можно в интерактивном режиме выбрать необходимое количество строк и столбцов для будущей таблицы. Если таблица очень большая и количество предлагаемых ячеек недостаточно, нужно воспользоваться опцией "Вставить таблицу" и в появившемся окне задать необходимое количество строк и столбцов. При необходимости создания сложной таблицы, состоящей из разнообразных комбинаций ячеек, то проще и быстрее нарисовать таблицу "вручную". Для этого служит кнопка-опция "Нарисовать таблицу". В этом режиме курсор приобретает вид карандаша. Можно превращать уже набранный текст в таблицу. Для этого необходимо выделить нужный блок текста и выбрать пункт меню "Преобразовать в таблицу". В появившемся окне надо задать параметры будущей таблицы. Форматирование текста в выделенных ячейках таблицы ничем не отличается от форматирования обычного текста документа. Тонкие настройки таблицы (параметры строк, столбцов, ячеек) можно произвести в окне "Свойства таблицы", которое открывается кнопкой "Свойства" на панели "Таблица".