
- •Лекция 3 Интерференция и дифракция световых волн
- •Вопрос 1. Электромагнитная природа света
- •Вопрос 2. Интерференция света. Когерентность. Интерференция света
- •Вопрос 3. Интерференция света в тонких пленках
- •Вопрос 4. Полосы равной толщины. Кольца Ньютона.
- •Вопрос 5. Применение интерференции в технике
- •Вопрос 6. Дифракция света. Дифракционная решетка. Дифракционный спектр
- •Дифракционная решетка – спектральный прибор
Вопрос 3. Интерференция света в тонких пленках
Наблюдаемое в природе радужное окрашивание тонких пленок (масляная пленка на воде, мыльные пузыри, оксидная пленка на металлах) объясняется интерференцией света, возникающей в результате отражения света от передней и задней поверхностей пленки (рис.3).
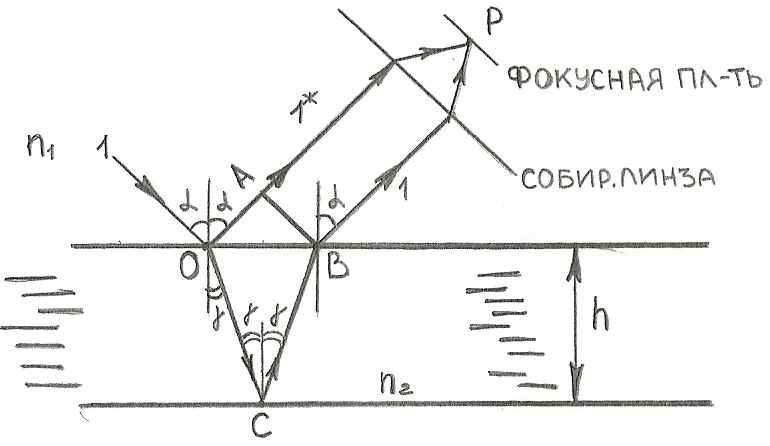
рис.3
На этом рисунке изображена тонкая плоскопараллельная прозрачная пленка, на которую падает плоская волна. В точке О волна частично отразится от верхней поверхности пленки(волна 1*), а частично преломится и отразится от задней ее поверхности в точке С, преломившись в точке В, войдет в воздух параллельно волне 1*.
Волны 1 и 1* – когерентны.
Если на их пути поставить собирающую линзу, то они будут накладываться в ее фокальной плоскости и дадут интерференционную картину, которая определяется их оптической разностью хода
![]() (8)
(8)
![]() обусловлен потерей полуволны при
отражении света от границы раздела
оптически более плотной среды.
обусловлен потерей полуволны при
отражении света от границы раздела
оптически более плотной среды.
Если
![]() ,
то потеря полуволны произойдет в точке
О и член будет со знаком “+”; если
,
то потеря полуволны произойдет в точке
О и член будет со знаком “+”; если ![]() ,
то потеря полуволны произойдет в точке
С и он будет иметь знак “-”.
,
то потеря полуволны произойдет в точке
С и он будет иметь знак “-”.
Вопрос 4. Полосы равной толщины. Кольца Ньютона.
Если положить одну плоскопараллельную пластинку на другую, а под один из концов верхней пластинки подложить небольшой предмет таким образом, чтобы между пластинками образовался воздушный клин (рис.4), то в этом клине можно наблюдать интерференционные полосы.
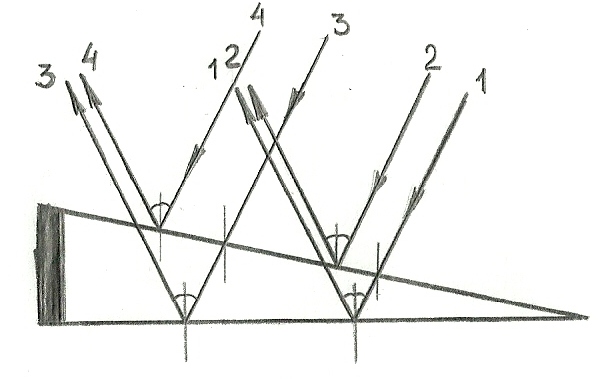
рис.4
В этом случае разность хода лучей определяется по формулам:
![]() (9)
(9)
d – толщина воздушного клинка
(9) - условие максимума.
![]() (10)
(10)
(10) - условия минимума.
Если допустить, что лучи падают на воздушный клин нормально (sinα=0) показатель преломления воздуха (n=1), тогда:
![]() (11)
(11)
На
границе соприкосновения стеклянных
пластин: d![]() 0
и ∆=
0
и ∆=
![]() –
поэтому наблюдается темная полоса
(min).
–
поэтому наблюдается темная полоса
(min).
Первая светлая полоса (κ=1)возникает при ∆=λ,
так
как
![]() ,
поэтому
,
поэтому
![]() .
Отсюда
получаем, что в этом месте толщина
воздушного клина d
=
.
Отсюда
получаем, что в этом месте толщина
воздушного клина d
= ![]() .
Именно такой воздушный промежуток
проходит
параллельно грани соприкосновения, и
световая полоса имеет вид прямой линии.
.
Именно такой воздушный промежуток
проходит
параллельно грани соприкосновения, и
световая полоса имеет вид прямой линии.
Вторая
светлая полоса
находится там, где толщина воздушного
клина достигает значения d=![]() λ,так
как при этом ∆=2
λ,так
как при этом ∆=2![]() (
(![]() )=
2d +
)=
2d +![]() .
.
Эти полосы, каждой из которых соответствует своя вполне определенная толщина клина или параллельной пластинки, называют полосами равной толщины.
Полосы равной толщины могут быть прямыми линиями, концентрическими окружностями, и иметь любую другую форму в зависимости от расположения точек, соответствующих d=const. Угол клина должен быть очень малым, иначе полосы равной толщины ложатся друг на друга и их нельзя различить. Полосы равной толщины можно получить, если наложить плосковыпуклую линзу с большим радиусом кривизны ( R=10-100 м) на плоскопараллельную пластинку (рис.5). В этом случае полосы равной толщины имеют вид колец, которые называют кольца Ньютона (рис.6).
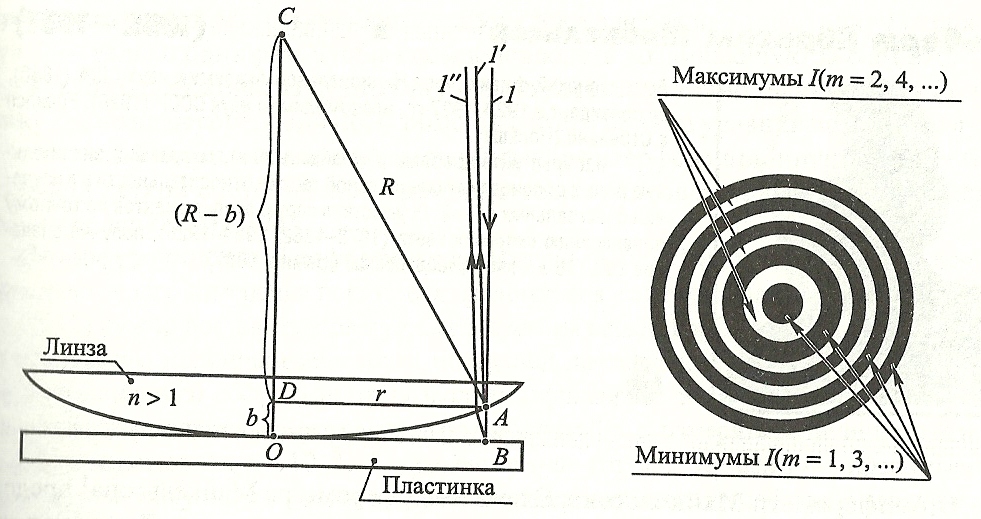
рис.5 и 6
Если на линзу падает монохроматический свет, то волны, отраженные от верхней и нижней границ этой воздушной прослойки, интерферируют между собой и их разность хода (∆) зависит от толщины воздушного клина. В отраженном свете при этом наблюдается следующая картина: в центре – черное пятно, окруженное чередующимися концентрическими светлыми и темными интерференционными кольцами убывающей ширины (рис.6). В проходящем свете картина обратная: все светлые кольца заменяются темными, а в центре – светлое пятно.
