
- •Лекция №2 Геометрическая оптика
- •Вопрос 1. Отражение света. Законы отражения.
- •Лучи падающий и отраженный лежат в одной плоскости с перпендикуляром, восстановленным в точке падения луча.
- •Угол отражения равен углу падения
- •Вопрос 2. Законы преломления света.
- •Экспериментально установлены следующие законы преломления света:
- •Вопрос 3. Полное (внутреннее) отражение света. Предельный угол полного отражения. Световоды.
- •Вопрос 4. Ход лучей в призме.
- •Вопрос 5. Линзы. Фокусное расстояние линзы.
- •Вопрос 6. Построение изображений в линзах.
- •Построение изображения точки в собирающей линзе.
- •Построение изображения предмета в собирающей линзе.
- •Построение изображения точки в рассеивающей линзе (рис. 17)
- •Вопрос 7. Оптическая сила линзы. Формула линзы. Линейное увеличение линзы
- •Формула линзы. Линейное увеличение линзы.
Вопрос 6. Построение изображений в линзах.
Световые лучи, идущие вблизи главной оптической оси, называют параксиальными (приосевыми). В дальнейшем будем рассматривать только такие лучи.
Построение изображения точки в собирающей линзе.
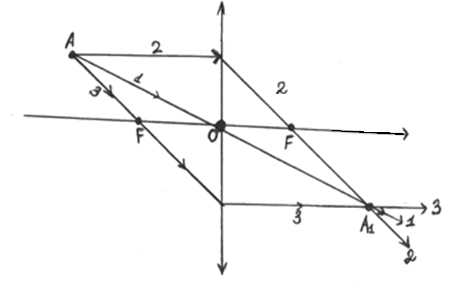
Рис. 13
Луч, идущей через оптический центр.
Луч, параллельный главной оптической оси.
Луч, проходящий через передний фокус собирающей линзы.
Построение изображения предмета в собирающей линзе.
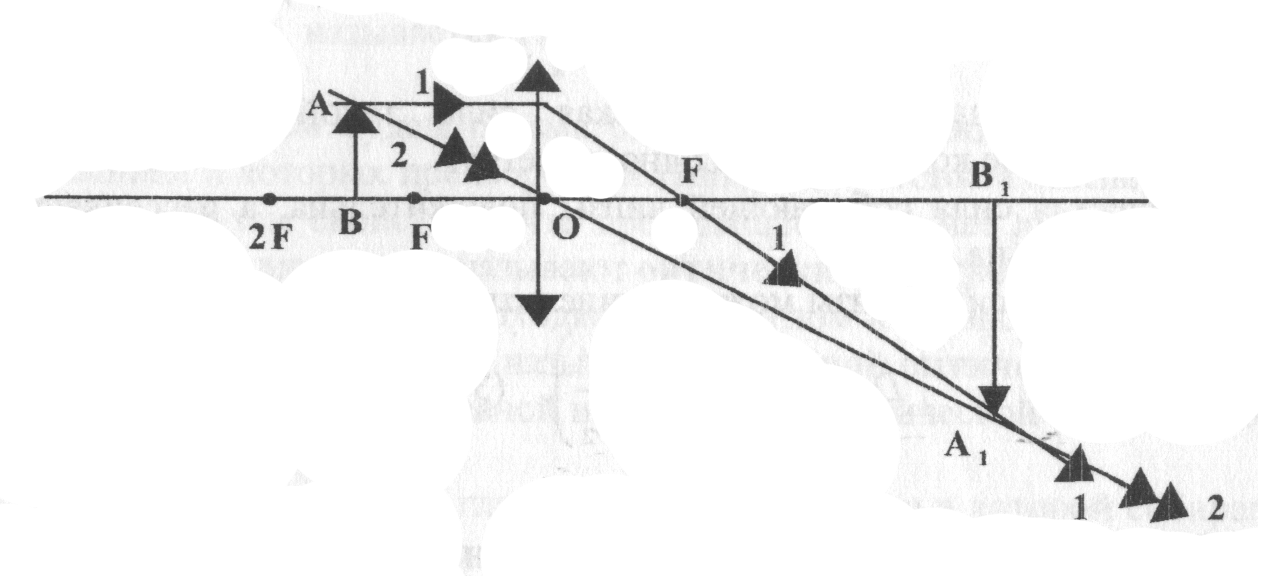
Рис. 14
ВО=d,
OB1=f
При d>2F изображение действительное, перевернутое, уменьшенное.
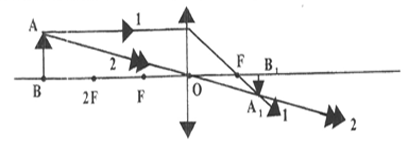
Рис. 15
Если d<2F, то изображение действительное, увеличенное перевернутое.
Если d<F, то изображение мнимое, прямое, увеличенное (рис. 16).
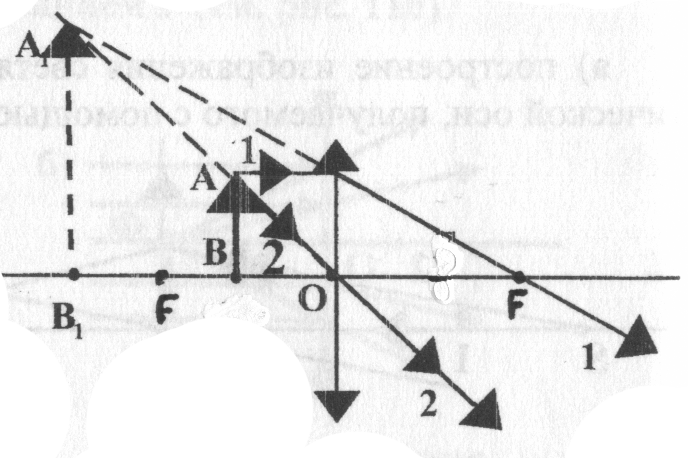
Рис. 16
Построение изображения точки в рассеивающей линзе (рис. 17)

Рис. 17
Построение изображения предмета в рассеивающей линзе (рис. 18)
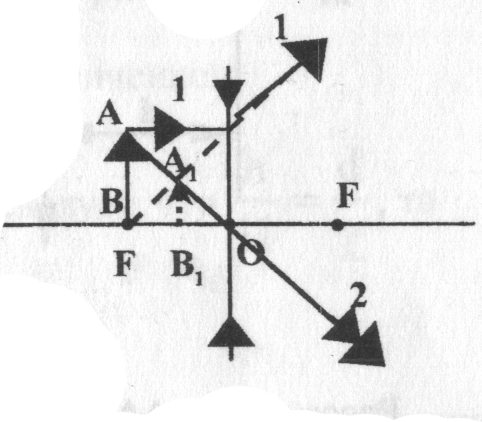
Рис. 18
Изображение всегда прямое, уменьшенное, мнимое.
Построение изображения точки лежащей на главной оптической оси (рис. 19 и рис. 20).
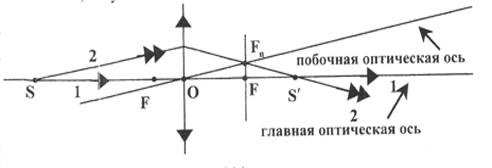 Рис.
19
Рис.
19
В собирающей линзе. (рис. 19)
В рассеивающей линзе. (рис. 20)
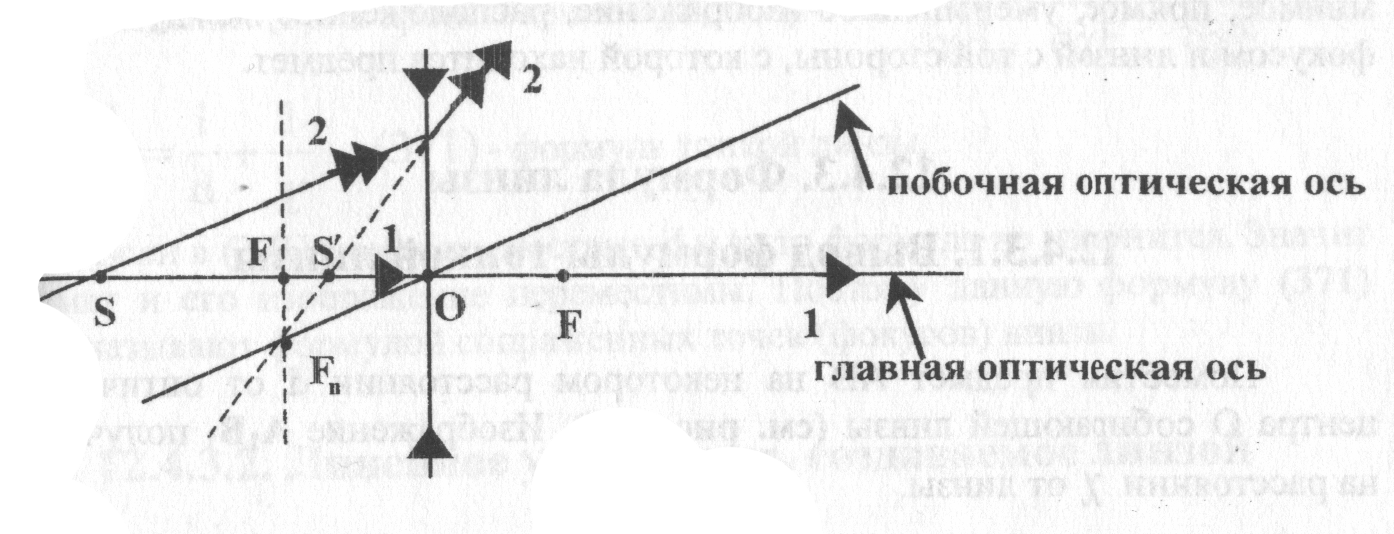 Рис.
20
Рис.
20
Вопрос 7. Оптическая сила линзы. Формула линзы. Линейное увеличение линзы
Из опыта известно, что линзы с более выпуклыми поверхностями преломляют сельнееи дают большее увеличение, чем линзы с меньшей кривизной.
У линзы с большей кривизной фокусное расстояние меньше.
Преломляющую способность линзы характеризуют оптической силой линзы.
Оптическая сила линзы D-величина, обратная фокусному расстоянию.
![]() (7)
(7)
![]()
![]()
1 дптр (диоптрия – оптическая сила линзы, фокусное расстояние которой равно 1м.)
Оптическую силу собирающей линзы условно считают положительной (фокус действительный), а оптическую силу рассеивающий (фокус мнимый) – отрицательный.
Оптическую силу линзы рассчитывают по формуле:
![]() (8)
(8)
n – относительный показатель преломления вещества линзы,
R1 и R2 – радиусы кривизны линзы. Радиусы выпуклых поверхностей считают положительным, вогнутых – отрицательными.
Из опыта известно, что общая оптическая сила 2-х линз, сложенных вместе, равна алгебраической сумме оптических сил этих линз: D=D1+D2 (9)
Формула линзы. Линейное увеличение линзы.
Из подобия треугольников (рис. 21)
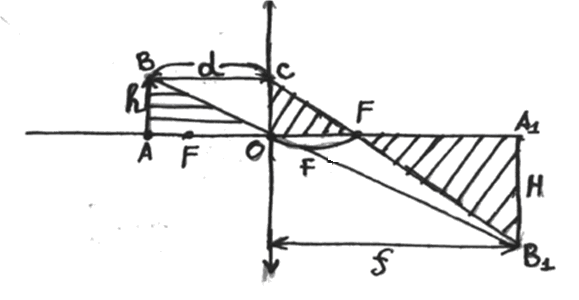
Рис. 21
∆A1B1F2
и ∆OCF2
следует:
![]() ,
аналогично ∆А1B1O
подобен ∆АВО;
,
аналогично ∆А1B1O
подобен ∆АВО;
![]() ;
Так как AB=AC, то:
;
Так как AB=AC, то:
![]() и
и
![]()
![]()
![]()
Разделим все слагаемые на f, имеем:
![]() (10)
(10)
или
![]() (11)
(11)
(11) – формула тонкой линзы.
Знак «+» для собирающей линзы, а «-» для рассеивающей линзы.
Г – линейное увеличение линзы:
![]() (12)
(12)
(12)
– отношение линейных размеров изображения
H к линейным размерам предмета h или Г
=![]()
Из треугольников (рис. 21) АВО и А1В1О имеем:
![]() (13)
(13)
Литература
Р.И. Грабовский. Курс физики.-С.пб.-М.-Краснодар: Издательство «Лань», 2006.
В.Д. Дмитриева. Физика.-М.: Издательство «Высшая школа», 2001.
А.Н. Ремизов. Курс физики, электроники и кибернетики. -М.: Издательство «Высшая школа», 1982.
Л.А. Аксенович, Н.Н. Ракина. Физика. -М.: Издательство «Дизайн Про», 2001.
А.С. Жданов, В.А. Маранджян. Курс физики. – М:Издательство «Наука», 1971.
М. Льоцци. История физики. – М.: Издательство «Мир», 1970.
