
- •1. Принципы расчёта поля излучения антенн. Основные электрические параметры передающих антенн
- •2. Особенности расчёта поля антенн в дальней зоне
- •3. Основные электрические параметры передающих антенн
- •Коэффициент полезного действия (кпд или ), коэффициент направленного действия (кнд или d), коэффициент усиления (ку или g).
- •6 Излучение антенных решеток
- •7)Линейная антенная решетка.Основные режимы излучения
- •8)Плоские антенные решетки
- •9)Входное сопротивление излучающего элемента
- •10)Коэффициент направленного действия линейных ар(2)
- •11)Влияние неравномерности амплитудного распределения на дн линейной ар
- •12)Влияние фазовых искажений на дн линейной решетки(1)
- •12)Влияние фазовых искажений на дн линейной решетки(2)
- •13.Неэквидистантные решетки
- •14.Сканирующие антенные решётки. Фазированные ар. Схемы возбуждения фазированных ар
- •15.Понятие о непрерывных линейных излучателях
- •16.Основы теории электрических симметричных вибраторов
- •17.Диаграммы направленности, кнд, входное сопротивление сэв
- •18.Конструктивные особенности реальных сэв
- •Излучение вибраторов, расположенных вблизи идеально проводящей плоскости. Несимметричные вибраторы
- •Варианты исполнения укв вибраторных антенн
- •Активные вибраторные антенны
- •Щелевые резонаторные антенны
- •25.Антенные вибраторные решётки укв диапазона. Схемы питания вибраторов.
- •26.Директорные антенны. Приёмные телевизионные антенны.
- •27.Логопериодические вибраторные антенны.
- •28.Вибраторные антенны вращающейся поляризации. Турникетные, спиральные антенны.
- •29.Понятие об излучающих раскрывах. Общие принципы расчёта излучения.
- •30.Излучающие раскрывы с неравноамплитудным и несинфазным распределением.
- •Принципы синтеза амплитудно-фазовых распределений. Условия существования точного решения. Сверхнаправленность.
- •Апертурные антенны. Разновидности. Принципы расчёта.
- •Антенны в виде открытого конца волновода
- •Рупорные антенны. Принцип действия, основные свойства рупорных антенн
- •Рупорные антенны с круговой поляризацией поля
- •Зеркальные параболические антенны. Геометрические свойства. Методы
- •Зеркальные параболические антенны
- •Двухзеркальные антенны. Методы расчёта.
- •Облучатели зеркальных антенн. Облучатели зеркальных антенн
- •37.Механизмы распространения радиоволн.
- •38.Напряжённость поля в точке приёма при распространении в свободном пространстве. Множитель ослабления. В условиях свободного пространства
- •39.Область пространства, существенно участвующая в формировании поля.
- •40.Распространение земной волны. Случаи высоко- и низкорасположенных антенн
- •41.Поле в освещённой зоне в приближении плоской земли. Учёт влияния сферичности земли.
- •42.Особенности распространения укв излучения земной волной. Формула Введенского. Учёт рельефа местности.
- •43 Распространение укв в городе.
- •44 Расчёт электромагнитных полей в случае низкорасположенного излучателя.
- •45 Методы расчёта полей в зонах полутени и тени
- •4 6 Строение атмосферы. Основные проявления влияния атмосферы на распространения радиоволн.
- •47 Распространение радиоволн в тропосфере
- •48 Электрические параметры ионосферы. Особенности распространения радиоволн в ионосфере
- •Ослабление радиоволн в атмосфере
- •Особенности передающих телевизионных антенн
1. Принципы расчёта поля излучения антенн. Основные электрические параметры передающих антенн
Будем изучать характеристики поля передающих антенн, рассматривая произвольную антенну. В инженерной практике наглядным является применение принципа суперпозиции.
Ввиду линейности уравнений Максвелла можно разбить проволочную антенну длиной L на элементарные участки d каждый из которых при малой толщине провода можно рассматривать как элементарный электрический вибратор (ЭЭВ, то же самое – элемент Гюйгенса), и далее найти результирующее поле путем суммирования всех элементарных полей с учетом их поляризаций, амплитуд и фаз. В локальной сферической системе координат (рис. 1.2) r, и , связанной с элементами декартовой системы x, y, z, ось которой совпадает с осью этого элементарного излучателя, комплексная амплитуда напряженности электрического поля имеет вид:
 . (1.1)
. (1.1)
В
(1.1)
– линейная координата вдоль провода,
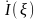 - комплексная амплитуда тока в выделенном
элементе, k
= 2/
– модуль волнового вектора,
– длина волны в свободном пространстве,
- комплексная амплитуда тока в выделенном
элементе, k
= 2/
– модуль волнового вектора,
– длина волны в свободном пространстве,
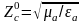 = 120
Ом в воздухе (характеристическое
сопротивление среды), j
– мнимая единица.
= 120
Ом в воздухе (характеристическое
сопротивление среды), j
– мнимая единица.
Напряженность магнитного поля в дальней зоне ЭЭВ связана с выражением (1.1):
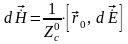 (1.2)
(1.2)
Результирующее поле определится суммированием полей элементарных участков:
 ,
и
,
и
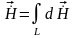 . (1.3)
. (1.3)
Выражение (1.3) представляет собой принцип суперпозиции.

В ряде случаев, когда распределение тока по антенне либо неизвестно, либо слишком сложно, но из каких-либо априорных соображений известно распределение поля вблизи антенны (такая ситуация возникает для апертурных антенн, в частности, для параболических), найти излучаемое антенной поле можно с помощью принципа эквивалентности. Согласно этому принципу излучение реальных электрических токов заменяется излучением эквивалентных поверхностных электрических и магнитных токов, распределенных в точках воображаемой произвольной поверхности S, окружающей антенну. Плотность этих токов имеет вид:
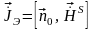 ,
и
,
и
 , (1.4)
, (1.4)
где
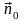 - единичная нормаль к поверхности S,
внешняя по отношению к области, занятой
антенной; ES,
HS
–
поле в точках на поверхности S.
- единичная нормаль к поверхности S,
внешняя по отношению к области, занятой
антенной; ES,
HS
–
поле в точках на поверхности S.
Разбивая поверхность S на элементарные площадки dS и рассматривая каждую площадку как совокупность двух элементарных излучателей – электрического и магнитного, можно найти полное поле во внешней области, суммируя поля, созданные отдельными элементами. Обычно учитывают токи только на части замкнутой поверхности S, где они наиболее существенны, причем эту часть поверхности выбирают совпадающей с фронтом волны, излучаемой антенной. В данном случае каждую элементарную площадку можно рассматривать как элемент волнового фронта – элемент Гюйгенса, электрическое поле которого в локальной системе координат при r << можно представить в виде:
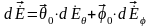
где
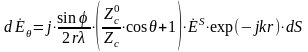 , (1.5)
, (1.5)
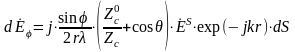 . (1.6)
. (1.6)
В формулах (1.5) и (1.6) Z°c – характеристическое сопротивление среды. Величина Zc характеризует отношение амплитуд полей ES и Hs. Результирующее электрическое поле находится как соответствующие интегралы по аналогии с (1.3).
