Вопрос 1 и 9. Односторонняя функция, Односторонняя функция с секретом. Определение, примеры.

Это отображение f:X→Y, такое что существует простой алгоритм вычисления значений функции f(x) и не существует простого алгоритма инвертирования функции f для почти всех y: f ^-1(y).

До сих пор не доказано существование односторонних функций.

ПРИМЕР

1) умножение f: Z*Z→Z, f(x,y)=x*y; 2) p – простые числа, a<p, f(x), f:Z_p→Z_p, f(x)=a^x(modp) – прямая задача возведения в степень O(n³), Обратная – логарифмирование субэкспоненциальной сложности; 3) Oneway function – односторонняя функция. Односторонняя функция с секретом k называется f:X→Y – отображение, зависящее от параметра k такое, что просто вычислить значение f_k(x) даже не зная k.

- даже не зная k;

- зная k просто ;

- не зная k сложно почти для всех y.

Эти односторонние функции с секретом называются trapdoorfunction. До сих пор не доказано их существование.

ПРИМЕР

N=p*q, p и q – простые числа примерно равной длины. , взаимопростые с (р-1)( q-1), р, q – секреты. E_(N,e):Z_N→Z_N, E_(N,e)(x)=x^e(modN). Прямая задача – вычисление E_(N,e)(x), T=O(n³), n - длины N; обратная задача - , где - субэкспоненциальной сложности, не зная p и q; зная p и q легко построить число d. , где - функция Эйлера,

, Теорема Эйлера: Если a взаимнопросто с N, тогда , .

Вопрос 2. Криптографическая хэш-функция. Определение. Отличие сильной хэш-функции от слабой.

- одностороння функция

Сложно найти - коллизия ХФ.

Сложно вычислить прообраз (односторонняя функция)

Слабой ХФ называется односторонняя функция, которая удовлетворяет следующим условиям:

, где n – некоторое число, V_n – бит последовательности длины n, V* - бит последовательности длины.

1) легко вычислить H(x);

2) фиксированный , где : трудно найти H(x)=H(x’)

Сильная ХФ это односторонняя функция, которая удовлетворяет следующим условиям:

1) Легко вычислить h(X);

2) трудно найти пару , : H(x)=H(x’)

Сильная также является слабой за счет 2-го условия, т.к. найти фиксированные коллизии нельзя.

Безопасность слабой ХФ

Найти коллизию k фиксированного х. Пербор х’ => различие H(x’)=H(x). Всего образов |V_n|=2ⁿ. В среднем противнику придется перебрать |V_n|/2 вариантов.

Если есть время Т, тогда T(n)=>n>log₂T+1, чтобы ХФ была безопасной должна выполняться функция.

Безопасность сильной ХФ

Найти коллизию . Перебор дает H(x)=H(x’). Всего образов |V_n|=2ⁿ. С вероятность 0,63 достаточно перебрать значений. . Чтобы ХФ была безопасной, должно выполняться

2^n/2>T=>n>log₂T

При одном и том же ресурсе противника сильная должна быть длинее в 2 раза, следовательно, снижается скорость ее работы.

Вопрос 3. Типовые конструкции криптографических хэш-функций.

ИСО/МЭК 10118-1 задается общая конструкция ХФ. |m|=L_m, |H(m)|=L_h.

1) дополнить структуру m до длины, кратной длине L₁(длина блока n) для того, чтобы после «резать» равными частями;

2) Разбить дополненную последовательность на блоки m=m₁||m₂||…||m_q;

3) определяем стартовой значение H₀=IV – строка длины L₂, H₁…H_q:|H_i|=L₂, H_i=φ(m_i; H_i-1);

4) H(m)=T(H_q), T:

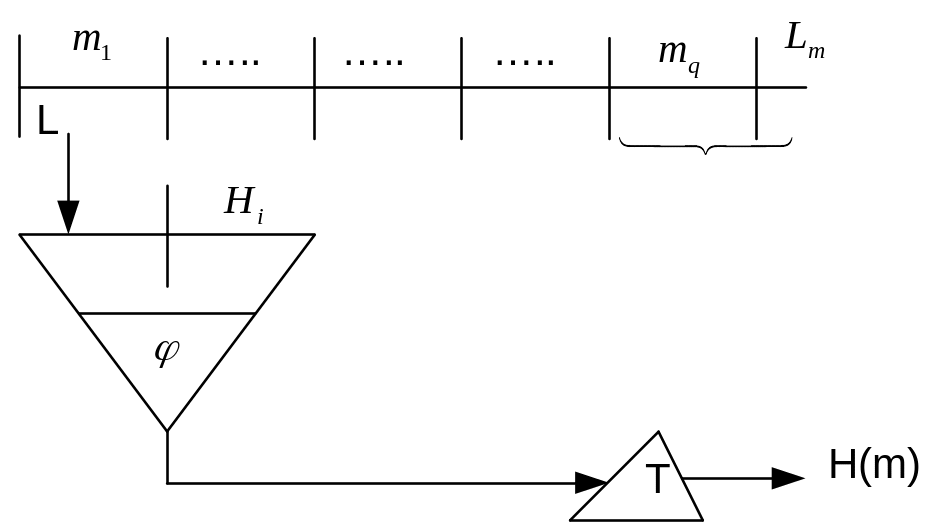
Для определения ХФ, определенной стандартом, необходимы условия:

1. выбрать L₁, L₂, L_h;

2. метод дополнения L₁;

3. стартовый вектор IV;

4. определение φ-шаговая функция;

5. Финальные преобразования T;

6. Padding – методы дополнения

L₁ и L₂ выбираются равными, и часто это значение равно L_h.

IV выбирается либо нулевой, либо заранее оговоренное значение.

Методы дополнения описаны в 10118-1, самый простой «Метод нуля».

Дополнение нулями при отсутствии финального преобразования приводит к тому, что значение ХФ без дополнения равно ХФ с дополнением до кратности.

Для того, чтобы противостоять этой атаки необходимо подать на вход длину сообщения.

Финальное преобразование часто опускаются, что приводит к атаке добавления сообщения.

ISO/IEC 10118-2 посвящен использованию построения алгоритма шифрования φ.

k_i зависит от H_i-1, m_i добавляется для того, чтобы избежать атаки на ХФ.

Этот вариант применим, когда уже есть реализация схемы шифрования.

В ISO/IEC 10118-3 сформулировано изготовление φ, т.е. специально для этой цели. «Заказные» ХФ. Приведены ХФ для следующих стандартов: SHA – 1(160бит), SHA – 256, SHA – 512, SHA – 384, RIPEMD – 128, RIPEMD – 160.

В ISO/IEC 10118-4 предлагается использовать в значениях ХФ модулярную арифметику. Предлагает вычислять φ следующим образом

(1), где A=const.

- m_i расшифровывается в два раза – B_i;

- каждый полубайт m_i дополняется полубайтом, состоящим из единиц (1111)₂;

- N произведение 2-х больших;

- е рекомендуется выбирать е или 257

Единственное достойинство модулярной арифметики в том, что она может быть удобной.

Идея: - отказались и перешли к (1) из-за того, что для «идеи» нашли много атак.

(1) – окончательный вариант.