51. Электрический поверхностный эффект

Рассмотрим проводник в виде шины (рис.18.8). Предположим, что 2a<<h, h<<l. По проводнику протекает ток I. В любом поперечном сечении характер распределения напряженности магнитного поля одинаков.

Требуется выяснить распределение напряженности электрического и магнитного полей по сечению шины.

Так как у шины имеется две границы, то могут возникать прямые и обратные волны. Поэтому решение дифференциальных уравнений второго порядка имеет вид:

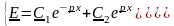(18.26)

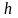
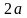
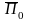
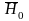
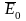
Рис. 18.8. Электромагнитное поле в проводнике с током

Разместим начало системы координат посредине шины и сориентируем ее таким образом, чтобы векторы напряженностей электрического и магнитного полей имели составляющие только по одной координате.

Постоянные интегрирования определим из граничных условий:

- при x=-a H=H₀;

- при x=a H=-H₀.

Тогда из системы уравнений (18.26) следует:

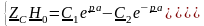
Следовательно,

(18.27)

Учитывая, что на границе шины

(18.28)

Рассмотрим, как изменяются соотношения E/E₀ и H/H₀ по сечению шины. Так как коэффициенты затухания и фазы для проводящей среды равны, то

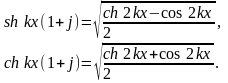
Тогда

, (18.29)

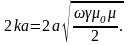
Так как величина a является числом, то характер зависимостей E/E₀ и H/H₀ определяется характеристиками материала шины и частотой. Эти зависимости представлены на рис. 18.9.

Так как ch p·0≠0, то напряженность электрического поля не уменьшается до нуля. В то же время sh p·0=0, поэтому напряженность магнитного поля в середине шины (при x=0) равна нулю.

2ka=0

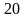
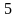
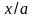
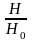
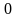
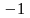
Рис. 18.9. Зависимости E/E₀ и H/H₀ от толщины шины

При ω=0 (постоянный ток) величина напряженности электрического поля определяется вектором плотности тока и не зависит от положения рассматриваемой области. Аналогичная картина наблюдается при частотах, близких к нулю. В этом случае говорят о квазистатическом распределении поля.

При повышении частоты картина распределения плотности тока, а, следовательно, и напряженности электрического поля меняется. Большее значение напряженностей наблюдается по края пластины и спадает во внутренней части. Возникает поверхностный эффект.

В другом случае (при ω→∞) ток будет протекать только по поверхности шины.

52. Применение теоремы Умова-Пойнтинга для определения активного и внутреннего индуктивного сопротивлений проводников при переменном токе

При протекании постоянного тока сопротивление R=l/γs.

При протекании переменного тока магнитное поле меняет распределение плотности тока и оказывает влияние, как на реактивную, так и на активную составляющие сопротивления.

Для определения активного и внутреннего реактивного сопротивлений проводников при протекании переменного тока используют теорему Умова-Пойнтинга в комплексной форме. Подсчитывается поток вектора Пойнтинга через боковую поверхность проводника на длине в 1 метр и делят его на квадрат тока, протекающего по проводнику. В результате получают комплексное сопротивление проводника на единицу длины:

(18.38)

Рассмотрим влияние протекания переменного тока на сопротивление прямоугольного проводника.

Поток энергии на границе проводника определяется вектором Пойнтинга

С учетом ранее сделанных допущений (2a<<h, h<<l), а также, что при стремится к единице, получим Следовательно, .

Волновое сопротивление .

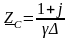При этом вектор Пойнтинга

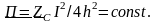
Тогда

Следовательно, полное сопротивление шины будет

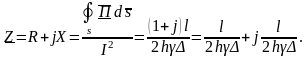(18.39)

Распределение протекающего тока показано на рис. 18.11.

Рис. 18.11. Распределение тока в толще проводника

Магнитное поле вытесняет ток на внешние поверхности проводника, увеличивая его сопротивление. Поэтому величину 2h∆ рассматривают как эквивалентное поперечное сечение проводника.