§4 Парабола
Параболой называется множество всех точек плоскости, каждая из которых равноудалена от заданной точки, называемой фокусом и заданной прямой, называемой директрисой.
Каноническое
уравнение параболы имеет вид
,
(51)
где число
,
равное расстоянию от фокуса
до директрисы
,
называется параметром
параболы. Координаты фокуса
.
Точка
называется вершиной параболы, длина
отрезка
- фокальный
радиус точки
,
ось
- ось симметрии
параболы.
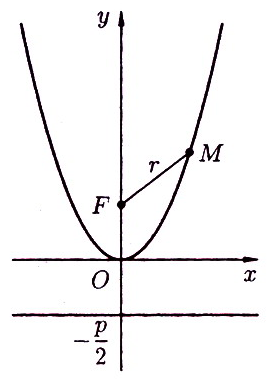
Рисунок 69 Рисунок 70
Уравнение директрисы
параболы имеет вид
;
фокальный радиус
вычисляется по формуле
.
В прямоугольной
системе координат парабола, заданная
каноническим уравнением
,
расположена так, как указано на рисунке
69.
Замечания.
1) Парабола,
симметричная относительно оси
и проходящая через точку
(рисунок 70), имеет уравнение
(52)
Уравнение директрисы:
,
фокальный радиус точки
параболы
.
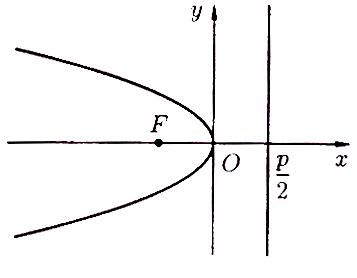
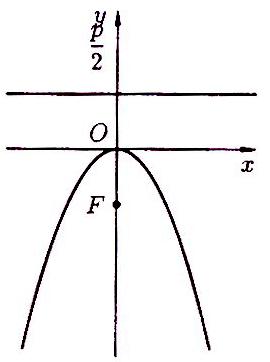
Рисунок 71 Рисунок 72
(53) 
(54)
3) На рисунках 73 – 76 приведены графики парабол с осями симметрии, параллельными координатным осям.
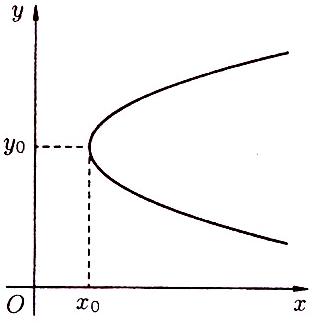
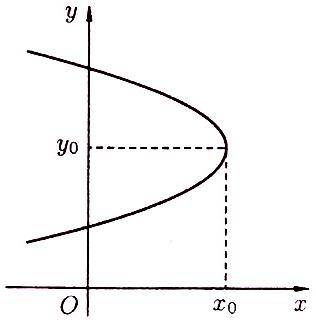
Рисунок 73 Рисунок 74
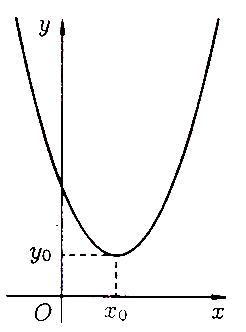
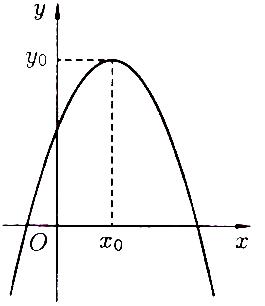
Рисунок 75 Рисунок 76
Практическое занятие № 5 Кривые второго порядка
Задача 1
Составить уравнение
окружности, проходящей через три точки
,
,
.
Решение:
Подставим координаты
точек
и
в данное уравнение:
.
От второго уравнения отняли первое уравнения и результат поставили на первое место. От третьего уравнения отняли первое уравнения и результат поставили на второе место. Третье уравнение оставили без изменения.
.
Ответ.
Задача 2
Привести уравнение
кривой к каноническому виду и изобразить
кривую, которая определяется уравнением:
.
Решение:
,
сгруппируем переменные.
,
вынесем за скобки.
,
в скобках дополним до полного квадрата.
,
сгруппируем по формуле полного квадрата.
,
,
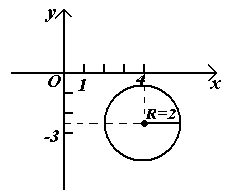
Уравнение окружность
с центром в точке
и
.
Рисунок 77
Задача 3.
Установить вид кривой по следующим уравнениям:
а)
; б)
;
в)
и сделать чертеж.
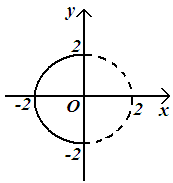
Решение.
а)
:
.
Возведем в квадрат правую и левую часть
уравнения.
.
Мы получили уравнения окружности с
центром в точке
и радиусом
.
Рисунок 78
б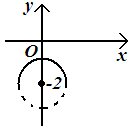
)
,
.
Возведем в квадрат правую и левую часть
уравнения.
.
Уравнения окружности
с центром в точке
и радиусом
.
Рисунок 79
в)
,
.
Возведем в квадрат правую и левую часть
уравнения.
.
Дополним до полного квадрата правую
часть.
.
.
Получили уравнения окружности с центром
в точке
и радиусом
.
Рисунок 80
Задача 4
Дано уравнение
эллипса
.
Найти:
а) длины его полуосей;
б) координаты фокусов;
в) эксцентриситет эллипса;
г) уравнения директрис и расстояние между ними;
д) точки эллипса,
расстояние от которых до левого фокуса
равно 12.
Р
ешение.
Разделив обе части уравнения на 1176 мы
получим уравнение эллипса в каноническом
виде
.
а) длины полуосей
эллипса
,
,
т.е.
,
.
б) координаты
фокусов. Так как
,
то
,
.
Следовательно,
и
.
Рисунок
81
в) эксцентриситет
эллипса. Так как
,
то
.
г) уравнения
директрис имеют вид
и
.
Тогда 
,
т.е.
и
;
расстояние между ними
.
д) точки эллипса,
расстояние от которых до левого фокуса
равно 12. По формуле
находим абсциссу точки, расстояние от
которой до точки
равно 12:
,
т.е.
.
Подставляя значение
в уравнение эллипса, найдем ординату
этой точки:
,
,
.
Условию задачи
удовлетворяет точка
.
Задача 5
Показать, что
уравнение
определяет эллипс, найти его оси,
координаты центра и эксцентриситет
(изобразить эллипс).
Р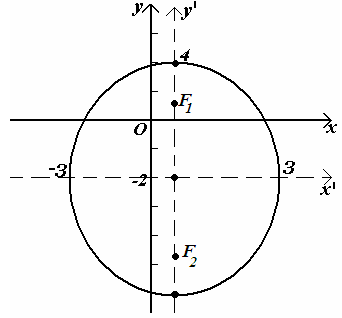
ешение.
Преобразуем данное уравнение кривой.
,
Сгруппировали переменные и вынесли за скобки
коэффициенты при наивысших степенях. В каждой скобке выделим полный квадрат.
.Раскроем
скобки.
,
.
Получили уравнение эллипса,
центр находится
в точке
.
Из уравнения находим:
,
и
,
.
Рисунок 82
Поэтому
.
Эксцентриситет эллипса
.
Задача 6
Составить уравнение
эллипса с центром в начале координат и
фокусами, лежащими на оси
.
Эллипс проходит через точки
и
.
Решение.
Уравнение эллипса
имеет вид:
.
Так как эллипс проходит через точки
и
,
то их координаты удовлетворяют уравнению
эллипса:
и
.
Умножая второе равенство на
и складывая с первым, находим
,
т.е.
.
Подставляя найденное значение
в первое уравнение, получаем
,
откуда
.
Таким образом, искомое уравнение эллипса
есть
.
Ответ.
Задача 7
Составить уравнение
эллипса, если известны его эксцентриситет
,
фокус
и уравнение соответствующей директрисы
.
Решение.
По теореме:
Отношение
расстояний от любой точки эллипса до
фокуса и соответствующей директрисы
равно эксцентриситету, рассмотрим любую
точку
принадлежащую эллипсу, значит
.
;
,
,
.
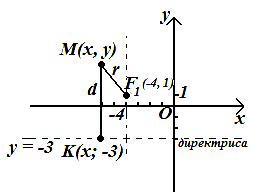Рисунок 82
Ответ.
Задача 8
Установить вид линии, которая определяется
следующим уравнением
и
изобразить ее.
Решение.
.
Возведем в квадрат правую и левую часть
уравнения.
.
Перенесем переменную в левую часть и
выделим полный квадрат.
,
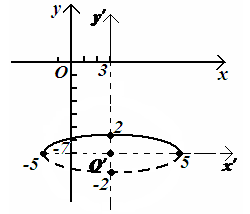
Получили уравнения эллипса.
Центр эллипса
находится в точке
.
.
.
Рисунок 83
Задача 9
Составить уравнение
эллипса, если известны его эксцентриситет
,
фокус
и уравнение соответствующей директрисы
.
Решение.
Точка
принадлежит эллипсу, если отношение
расстояний до фокуса и соответствующей
директрисы равно
,
т.е.
.
,
,
Рисунок 84
.
Ответ.
.
Задача 10
Дано уравнение
гиперболы
.
Найти:
а) длины его полуосей;
б) координаты фокусов;
в) эксцентриситет гиперболы;
г) уравнения асимптот и директрис; и нарисовать кривую.
Решение.
Разделив обе части
уравнения на 16, приведем уравнение
гиперболы к каноническому виду
:
.
а) длины его полуосей
,
,
т.е.
,
;
б) координаты
фокусов. Используя соотношение
,
находим
,
т.е.
.
Координаты фокусов:
и
;
в) эксцентриситет
гиперболы. По формуле
находим
;
г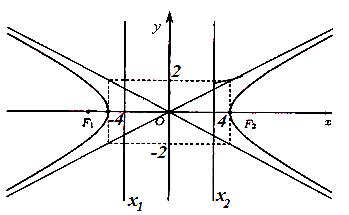
)
уравнения асимптот и
директрис найдем по формулам
и
:
и
.
Рисунок 85
Задача 11
Составить уравнение гиперболы, если ее фокусы лежат на оси и расстояние между ними равно 10, а длина действительной оси равна 8.
Решение.
Искомое уравнение
гиперболы имеет вид
.
Согласно условию
,
;
,
.
Из соотношения
найдем мнимую полуось
:
,
,
.
Получаем
- уравнение гиперболы.
Ответ.
Задача 12
Найти уравнение
гиперболы, фокусы которой находятся в
точках
и
,
а длина мнимой оси равна 6.
Решение.
Центр гиперболы
лежит на прямой
,
параллельной оси
.
Уравнение гиперболы имеет вид
.
По условию
,
.
Расстояние между фокусами равно 14, т.е.
,
.
Используя соотношение
,
находим
:
,
.
Центр гиперболы делит расстояние между
фокусами пополам. Поэтому
,
.
Записываем уравнение гиперболы:
.
Ответ.
Задача 13
Найти угол между асимптотами гиперболы, если ее эксцентриситет равен 2.
Решение.
Уравнения асимптот
гиперболы имеют вид
.
Найдем отношение
,
воспользовавшись формулами
,
и условием
:
.
Отсюда
,
т.е.
.
Имеем:
.
Следовательно, уравнения асимптот
гиперболы есть
и
.
Угол
между асимптотами найдем через угловые
коэффициенты по формуле
,
.
Ответ.
Задача 14
Дан эллипс
.
Найти уравнение гиперболы, вершины
которой находятся в фокусах эллипса, а
фокусы гиперболы – в вершинах данного
эллипса.
Рисунок 86
Решение.
Найдем координаты
вершин
и
и фокусов эллипса, записав его уравнение
в канонической форме
.
Имеем
,
;
,
.
Из соотношения
находим
:
,
.
Можно записать:
,
,
,
.
Обозначим через
,
,
- соответственно полуоси гиперболы и
половину расстояния между ее фокусами.
Тогда, согласно условиям задачи, можно
записать:
,
т.е.
и
,
т.е.
.
Из соотношения
находим
,
поэтому
,
.
Подставляя найденные значения
и
в уравнение
,
находим
- искомое уравнение гиперболы.
Ответ.
Задача 15
Дано уравнение
гиперболы
.
Найти:
а) длины его полуосей;
б) координаты фокусов;
в) эксцентриситет гиперболы;
г) уравнения асимптот и директрис;
д) сделать чертеж.
Решение.
,
,
- каноническое
уравнение гиперболы. Центр гиперболы
находится в точке
.
а) длины полуосей
гиперболы.
;
.
б) координаты
фокусов. Так как
.
и
.
в) эксцентриситет
гиперболы.
г) уравнения асимптот и директрис.
,
- уравнения асимптот.
;
- уравнения директрис.
д) сделать чертеж
Рисунок 87
Задача 16
Составить уравнение
гиперболы, если известны ее эксцентриситет
,
фокус
и уравнение соответствующей директрисы
.
Решение.
При решении используем теорему. Отношение расстояний от любой точки гиперболы до фокуса и соответствующей директрисы равно эксцентриситету.
Так как точка
принадлежит гиперболе, то
,
где
- расстояние от точки
до
,
- расстояние от точки
до прямой
.
Таким образом
;
.
.
,
,
,
,
.
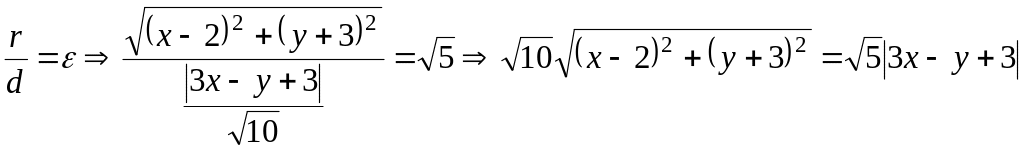Ответ.
Задача 17
У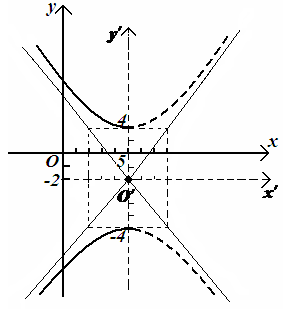
становить
и нарисовать линию, которая определяется
уравнением
.
Решение.
.
,
,
Рисунок 88
.
Уравнение гиперболы, центр в точке
.
.
З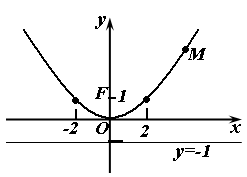
адача
18
Дана парабола
.
Найти координаты ее фокуса, уравнение
директрисы, длину фокального радиуса
точки
.
Решение.
Парабола задана
каноническим уравнением:
.
Следовательно,
,
.
Используя формулы, координаты фокуса
;
Рисунок 89
уравнение директрисы
есть
;
фокальный радиус
точки
равен
.
Ответ.
,
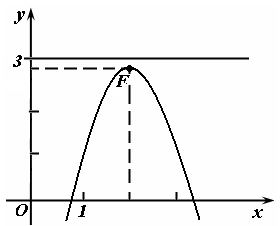
Задача 19
Найти вершину,
фокус и директрису параболы
,
построить эскиз параболы.
Решение.
Преобразуем уравнение , выделив в правой части полный квадрат:
,
т.е.
или
- уравнение параболы с вершиной в точке
:
,
.
Прямая
является осью симметрии параболы.
Рисунок
90
Координаты фокуса
,
,
т.е.
.
Уравнение директрисы
,
т.е.
.
График изображен
на рисунке 90.
Ответ.
,
,
Задача 20
Составить уравнение
параболы, если даны ее фокус
и директриса
.
Решение.
Точка лежит на параболе, если она равноудалена от фокуса и директрисы .
Таким образом,
точка
лежит на параболе, если
:
и
.
,
Возведем в квадрат правую и левую части уравнения.
,
,
.
Ответ.
З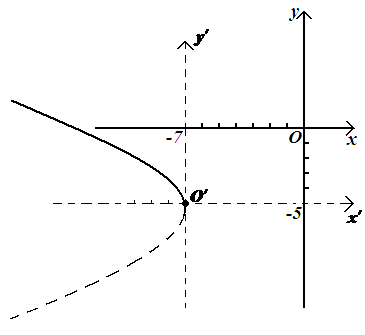
адача
21 Установить
и изобразить линию, которая определяется
уравнением:
.
Решение.
.
,
.Получили уравнение
параболы в каноническом виде, центр
которой находится в точке
.
.
Рисунок
91