
Методические указания / ZubKol
.pdf
4. Зубчасті колеса просторових передач Найбільш поширені просторові передачі це черв’ячні, бо вони
мають великі передаточні відношення. Приклади черв’яків та черв’ячних коліс наведені на рис. 11 та рис. 12.
а б Рисунок 11 – Черв’як: а – циліндричний, б – глобоїдний.
Рисунок 12 – Колесо черв’ячне
На креслениках зубчастих коліс обов’язково подається таблиця з параметрами зубчастого колеса. Розташовується вона впритул до правої кромки рамки кресленика, на відстані 20 мм від верхньої кромки рамки. Висота строк не менше ніж 7 мм. Кількість строк залежить від виду колеса. Ширина таблиці 110 мм. Таблиця розбивається на три колонки. Схему розміщення таблиці з параметрами зубчастого колеса наведено на рис. 13.
9
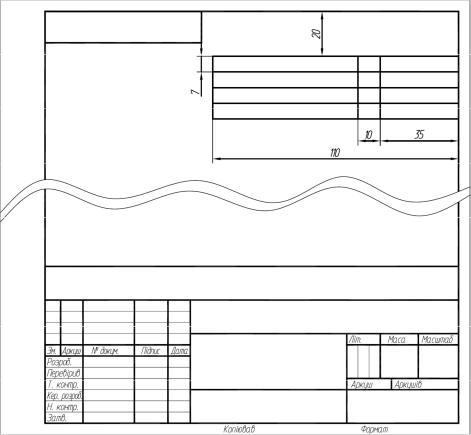
Рисунок 13 – Схема розміщення таблиці з параметрами зубчастого колеса
В першій колонці записується назва параметру, в другій – його позначення, в третій – його величина.
Приклад таблиці з параметрами циліндричного зубчастого колеса зі стандартним вихідним контуром наведений в таблиці 1.
Таблиця 1.
Модуль |
m |
|
Кількість зубців |
z |
|
Нормальний вихідний контур |
- |
|
Коефіцієнт зміщення |
|
|
Ступінь точності |
- |
|
Дані для контролю взаємного |
|
|
розташування різнойменних |
|
|
профілів зубців |
|
|
Ділильний діаметр |
d |
|
Інші довідкові дані |
|
|
Приклад таблиці з параметрами циліндричного зубчастого колеса з нестандартним вихідним контуром наведений в таблиці 2.
10
Таблиця 2.
Модуль |
|
m |
|
Число зубців |
z |
|
|
|
Кут профілю |
α |
|
контур |
|
|
|
Коефіцієнт висоти головки |
ha* |
|
|
Коефіцієнт граничної висоти |
hL* |
|
|
вихідний |
|
|
|
Коефіцієнт радіуса кривини |
ρ * |
|
|
перехідної кривої |
f |
|
|
|
|
||
|
|
|
|
Нормальний |
|
|
|
Коефіцієнт радіального зазору |
c* |
|
|
|
|
|
|
Коефіцієнт товщини зубця по |
S* |
|
|
ділильному колу |
|
||
|
|
||
|
|
|
|
Коефіцієнт зміщення |
χ |
|
|
Ступінь точності |
- |
|
|
Дані для контролю взаємного розташу- |
|
|
|
вання різнойменних профілів зубців |
|
|
|
Дані для контролю по нормам точності |
|
|
|
Ділильний діаметр |
d |
|
|
Інші довідкові дані |
|
|
|
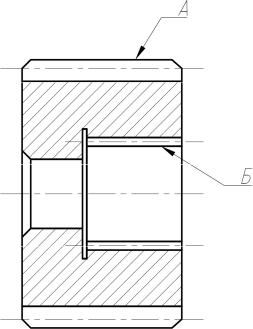
Якщо зубчасте колесо має два і більше вінців одного вида (рис. 14), значення параметрів розміщуються в окремих графах (колонках) для кожного вінця (табл. 3).
Рисунок 14 – Приклад зубчастого колеса з двома вінцями
11

|
|
|
|
|
|
|
Таблиця 3 |
|
|
|
|
|
|
|
|
|
|
Зубчастий вінець |
|
|
- |
|
А |
|
Б |
|
Модуль |
|
|
m |
|
|
|
|
|
Число зубців |
|
|
z |
|
|
|
|
|
Нормальний вихідний контур |
|
- |
|
|
|
|
|
|
Коефіцієнт зміщення |
|
|
χ |
|
|
|
|
|
Ступінь точності |
|
|
- |
|
|
|
|
|
Дані для контролю взаємного розташу- |
|
|
|
|
|
|
|
|
вання різнойменних профілів зубців |
|
|
|
|
|
|
|
|
Ділильний діаметр |
|
|
d |
|
|
|
|
|
Інші довідкові дані |
|
|
|
|
|
|
|
|
Порядок виконання креслеників зубчастих коліс. |
||||||||
1. Визначаємо |
основні |
параметри |
|
циліндричного |
||||
зубчастого колеса. Ними є модуль передачі, кількість зубців та діаметр ділильного кола. Кількість зубців z рахуємо. Вимірюємо діаметр виступів da , та за формулою (“± ” в знаменнику формули
верхній знак беремо для зовнішнього зачеплення, а нижній – для внутрішнього)
da = m(z ± 2)
визначається модуль передачі
m = da z ± 2
2.На форматі А4 розміщуємо таблицю параметрів.
3.Визначаємо головний вид та кількість необхідних проекцій зубчастого колеса.
4.Зображуємо зубчасте колесо з необхідними розрізами.
5.Наносимо необхідні розміри елементів зубчастого колеса.
6.Вказуємо шорсткість виконання поверхонь зубчастого колеса.
7.Заповнюємо основний напис кресленика.
8.Здаємо кресленик на перевірку викладачу.
Підписаний викладачем кресленик підшиваємо до альбому робіт з інженерної графіки. Формули для розрахунків наведені в додатку 1, приклади креслень зубчастих коліс наведені в додатку 2. Кресленики можна виконувати як з натури, так і по варіантам завдань в додатку 3.
12

Додаток 1
Формули для розрахунку конічних прямозубих коліс з кутом між осями 90°.
Максимальне значення модуля передачі mmax = mcp + b sinϕ1, z1
|
передаточне число u = |
z2 |
, де |
z = |
d1 |
, |
z |
|
|
|
= |
d2 |
, |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
1 |
|
|
m |
|
|
|
2 |
|
|
m |
|
|
||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
діаметри ділильних кіл: |
|
d1 = mz1, d2 = mz2. |
|
|
||||||||||||||||||||||||||||||
|
Діаметри кіл виступів: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
De1 = d + 2mmax cosϕ1 = mmax(z1 + 2cosϕ1), |
|
|
||||||||||||||||||||||||||||||||
De2 |
= d2 + 2mmax cosϕ2 = mmax(z2 + 2cosϕ2) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Діаметри кіл впадин: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Di1 = d1 − 2,4mmax cosϕ1 = mmax(z1 − 2,4cosϕ1), |
|
|
||||||||||||||||||||||||||||||||
|
Di 2= d2 − 2,4mmax cosϕ2 = mmax(z2 − 2,4cosϕ2) |
|
|
||||||||||||||||||||||||||||||||
|
Кут початкових конусів: tgϕ = |
z1 |
, tgϕ |
|
= |
z2 |
. |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
z |
2 |
|
|
|
|
|
|
2 |
|
|
|
|
z |
|
|
||||||
|
Кут додаткових конусів: ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
1 |
|
|
|
|
. |
|||||||||
|
|
|
|
= 90O − γ |
1 |
ϕ |
д2 |
= 90O − γ |
2 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
д1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Кут конусі виступів (кут зовнішніх |
|
конусів): αн1 =ϕ1 + γ1, |
||||||||||||||||||||||||||||||||
αн2 =ϕ2 +γ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Кут конусів впадин: αвп1 =ϕ1 −γ1, αвп2 =ϕ2 −γ2. |
|
|
||||||||||||||||||||||||||||||||
|
Кут головки зубця tgγ1 = |
m |
= |
|
2sinϕ1 |
= |
2sinϕ2 |
. |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
L |
|
z |
|
|
|
|
|
|
|
z |
2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
1,2m |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Кут ніжки зубця tgγ1 = |
=1,2tgγ2. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Крок по |
ділильному |
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
висота зубця h = 2,2m, |
||||||||||||||||
|
колуt = πm , |
|
|||||||||||||||||||||||||||||||||
Довжина зубця b ≈ (5 6)m, |
|
|
b < |
L |
|
, де L – довжина утворюючої |
|||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||
початкового конуса |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
L = |
d1 |
= |
d2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2sinϕ1 |
2sinϕ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Формули для розрахунку параметрів черв’ячної передачі.
Передаточне число u = |
z2 |
, де |
z −число зубців на |
|
|||
|
z1 |
|
2 |
|
|
|
черв’ячному колесі, z1 −число заходів червяка, модуль передачі m = Pπz , де - коловий крок черв’ячного колеса.
13

|
|
|
d1 + d2 |
|
|
|
Прод. додатку 1 |
Міжосьова відстань a |
w |
= |
= m( |
z2 |
+ q |
), де q - коефіцієнт |
|
2 |
|
2 |
|||||
|
|
|
|
|
|||
|
|
|
|
|
|
діаметра черв’яка і визначається за формулою q= dд1 . Величину q
m
знаходять в залежності від модуля згідно з ГОСТ 2144-76. Розрахунковий модуль черв’яка m: 4, 5, 6, 7, 8, (9), 10, 12, (14), 16, (18), 20. Коефіцієнт діаметра черв’яка q: 8, 9, 10, 12, 14, 16, 20.
Осьовий крок черв’яка P = πm , хід витка черв’яка
S = Pz1 = πmz1.
Висота головки витка черв’яка h′ = m; висота ніжки витка h′′ =1,2m.
Діаметр ділильного циліндра черв’яка |
d = |
z1m |
= |
|
S |
. |
|||||
|
|
||||||||||
|
|
|
|
|
|
1 |
tgλ |
|
πtgλ |
||
|
|
|
|
|
|
|
д |
|
|
д |
|
Кут підйому гвинтової лінії на ділильному циліндрі |
|||||||||||
tgλ |
= |
z1ms |
= |
S |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
д |
|
dд1 |
πdд1 |
|
|
|
|
|
|
||
Діаметр зовнішнього циліндру черв’яка de = d1 + 2m. Довжина нарізної частини черв’яка b:
b ≥ (11+ 0,06z2)m + |
для z1 =1 або z1 = 2; |
b ≥ (12,5+0,09z2)m+ |
для z1 =3 або z1 = 4; |
= 25 мм , якщо модуль менше 10мм, = 40 мм , якщо модуль менше 16мм та = 50 мм , якщо модуль більше 16мм.
Позначення черв’яка:
ZA - архімедів черв’як з кутом профілю αx ; ZJ - евольвентний черв’як з кутом профілю αn ;
ZN1 - конволютний черв’як з прямим профілем витка та кутом профілю αnT ;
ZN 2 - конволютний черв’як з прямим профілем впадин витка та кутом профілю αnT ;
ZT - циліндричний черв’як з зачепленням Новикова;
ZK- конічний черв’як згідно з ГОСТ 18498-73.
Діаметр ділильного кола в середній площині колеса d2 = z2ms .
Діаметр кола виступів в середній площині колеса
De = d2 + 2ms .
14

|
|
|
|
|
|
Прод. додатку 1 |
||
Діаметр |
кола |
виступів |
по |
краям |
зубців |
колеса |
||
Ds = De + (d2 − 2,5ms)(1− cosδ ). |
|
|
|
|
||||
Половина кута бокових скосів колеса δ = |
(0,04z2 |
+ 2,6)t0 |
. |
|||||
dд1 + t0 |
||||||||
|
|
|
|
|
|
|||
Довжина зубця біля основи l = de sinδ . Радіус кривини поверхні вінця по виступах зубців R1 = d21 − ms. Радіус кривини поверхні вінця по впадинах R2 = d21 +1,25ms . Висота зубця h = 2,25ms .
15
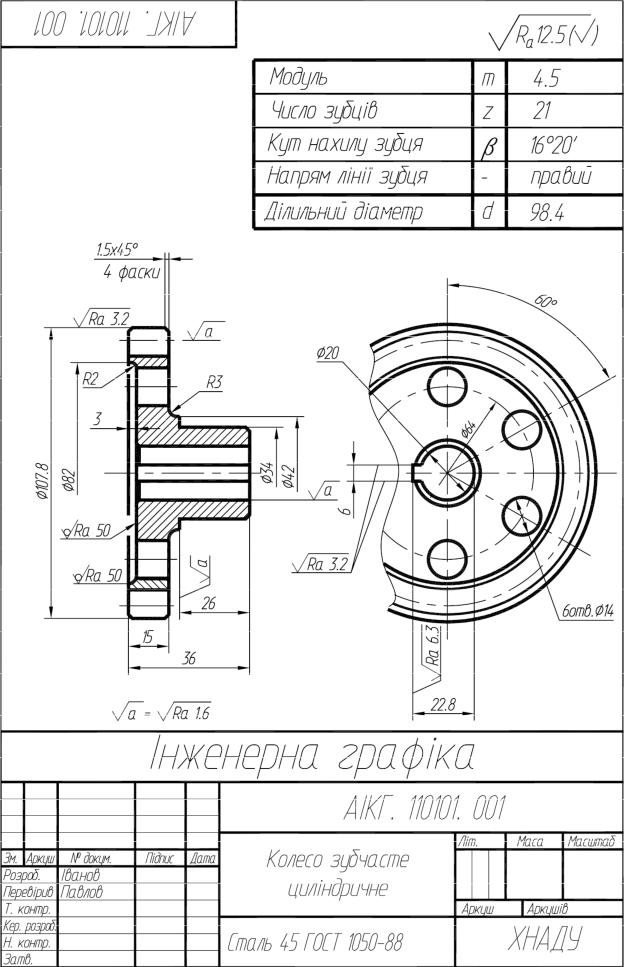
Додаток 2
16
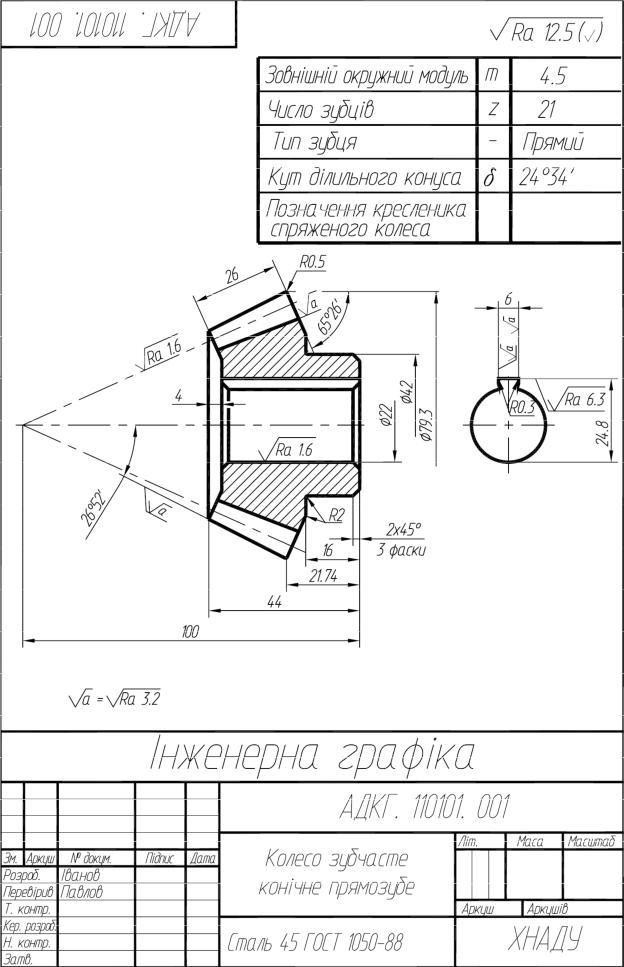
Прод. додатку 2
17
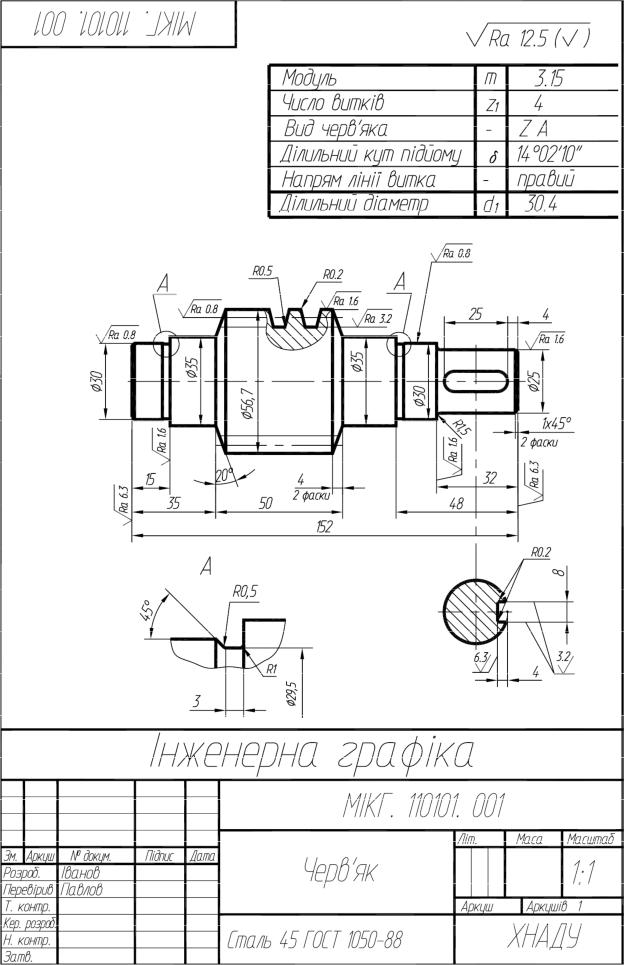
Прод. додатку 2
18
