154. При низких температурах теплоёмкость твёрдого тела зависит от температуры по закону
*A)
, т.к. новые моды упругих колебаний
оказываются возбуждёнными;
155. При высоких
температурах
теплопроводность твердого тела зависит
от температуры по закону
...
*C)
,
т.к. энергия колебаний ~T,
а количество возбуждённых мод не
меняется;
156. Между свободной
и валентной зонами находится запрещённая
зона шириной
=1,1
эВ. Валентная зона при
заполнена на половину. Кристалл является
. . .
*A) проводником;
157. Между свободной и валентной зонами находится запрещённая зона шириной = 5 эВ. Валентная зона при заполнена полностью. Кристалл является . . .
*C) изолятором;
158. В одновалентных металлах валентная зона заполнена …
*А) наполовину;
159. Теплоёмкость электронного газа в металлах …
*В) С~Т,
т.к. средняя энергия теплового движения
электронов в металле
;
160. Отношение теплоёмкости вырожденного электронного газа и теплоёмкости не вырожденного классического газа равно:
*А)
;
161. Отношение электронной и решеточной теплоёмкостей для твёрдого тела при высоких температурах составляет …
*С)
;
162. В собственном полупроводнике проводимость обусловлена переходом электронов
*C) из валентной зоны в зону проводимости;
163. Носителями тока в собственном полупроводнике являются …
*A) электроны в зоне проводимости и дырки в валентной зоне;
164. Для невырожденного полупроводника функция распределения электронов по энергиям в зоне проводимости имеет вид…
*А)
;
165. Для электронов в зоне проводимости невырожденного полупроводника следует применить распределение …
Укажите все возможные варианты.
*B) Ферми-Дирака; *C) Максвелла
166. Химический потенциал собственного полупроводника при Т=0 находится
*B) в середине запрещенной зоны;
167. Концентрация электронов собственного полупроводника зависит от температуры следующим образом …
*А)
;
168. Концентрация дырок в валентной зоне собственного полупроводника зависит от температуры следующим образом:
*А)
;
169. Формула
представляет собой зависимость
химического потенциала от температуры
для ...
*A) собственного полупроводника; (примесного полупроводника n-типа?)
170. Концентрация электронов в зоне проводимости собственного полупроводника возрастает с повышением Т за счёт перехода электронов
*B) из валентной зоны в зону проводимости;
171. Ширина
запрещённой зоны германия
эВ.
Отсчет энергии от дна зоны проводимости.
Химический потенциал при Т=0
равен ... эВ. Округлить до сотых.
Ответ: - 0,37
172. При увеличении температуры основная причина роста электропроводности собственного полупроводника …
*А) увеличение концентрации носителей тока;
173. Для получения полупроводника n-типа подбирают пятивалентную примесь, донорный уровень которой находится ...
*В) в запрещённой зоне вблизи дна зоны проводимости;
174. Концентрация электронов в зоне проводимости примесного проводника n-типа в области низких температур увеличивается за счёт перехода электронов …
*С) с донорного уровня в зону проводимости;
175. Для получения полупроводника p-типа подбирают трехвалентную примесь, акцепторный уровень которой находится …
*С) в запрещённой зоне вблизи потока валентной зоны;
176. Концентрация дырок в валентной зоне полупроводника p-типа в области низких температур увеличивается за счёт перехода электронов …
*С) из валентной зоны на акцепторный уровень; (в зону проводимости?)
177. Формула для концентрации электронов в зоне проводимости полупроводника n-типа имеет вид ...
*A)
;
(!) 178. На рисунке
представлены распределения Ферми-Дирака
по состояниям для двух систем частиц;
,
.
Отношение масс частиц
=
... (Ответ: 2)
<n>
ε
(!) 179. На рисунке
представлены распределения Ферми-Дирака
по состояниям
для двух систем частиц;
,
.
Отношение концентраций
... (Ответ: 8)
<n>
ε
(!) 180. На рисунке представлены распределения Ферми-Дирака по энергиям для двух систем частиц; , . Отношение концентраций (Ответ: 8)
F
ε
(!) 181. На рисунке
представлены распределения Ферми-Дирака
по энергиям для двух систем частиц ;
,
.
Отношение концентраций
=
(Ответ: 2)
F
ε
(!) 182. Энергия
Ферми металла
эВ, квазиимпульс электронов при этой
энергии
кг·м/c.
Масса свободного электрона
кг,
эффективная масса электрона
.
Отношение
равно ... Ответ округлить до целых.
Ответ: 3
(!) 183.
Энергия Ферми металла
эВ.
Эффективная масса электронов
.
Максимальная скорость электронов при
Т=0 равна … км/с. Ответ округлить до
сотен.
Ответ: 1900
(!) 184.
Энергия Ферми металла
эВ.
Эффективная масса электронов
.
Средняя скорость электронов при Т=0
равна … км/с. Ответ округлить до сотен.
Ответ: 1300
(!) 185. Энергия
Ферми для меди
,
для цинка
.
Эффективная масса электронов
.
Отношение концентраций свободных
электронов n2/n1
равно … . Ответ округлить до целых.
Ответ: 2
(!) 186.
Энергия
Ферми для меди
.
Средняя скорость электронов при Т=0
равна … . Ответ округлить до десятых.
Ответ: 4,2 - запятая
(!) 187. Средняя
скорость электронов в калии
при Т=0 равна 1,2эВ. Эффективная масса
.
Средняя скорость электронов при Т=0
равна … км/с. Ответ округлить до сотен.
Ответ: 600
(!) 188. Импульс,
соответствующий энергии Ферми
Масса электрона
.
Средняя энергия электронов равна …
эВ. Ответ округлить до целых.
Ответ: 6
(!) 189. Если абсолютную температуру абсолютно черного тела увеличить в n=2 раза, его энергетическая светимость увеличивается в k раз.
Ответ: 8
(!) 190. Максимум
спектральной энергетической
светимости излучения Солнца находится
при
мкм. Постоянная в законе смещения Вина
b
=
Температура
на поверхности Солнца приблизительности
равна … К.
Ответ: 5800
(!) 191. Температура
абсолютного черного тела равна
Т=
К. Постоянная в законе смещения Вина в
=
Максимум спектральной плотности излучения находится при частоте
*А)
(!) 192. Среднее
время пролета валентного электрона
в поле действия ядра в кристалле
Ширина валентной зоны
.
Постоянная Планка
.
Ответ округлить до десятых.
Ответ: 1,6 – запятая.
(!) 193.
В кристаллическом натрии электрон в
состоянии
1S
находится в поле действия ядра в среднем
Ширина соответствующей уровню 1S
энергетической зоны равна … .
.
*В)
(!) 194. Ширина
разрешенной энергетической
зоны
в одновалентном кристалле имеется N=
атомов. Расстояние между соседними
подуровнями в зоне равно
* В)
(!) 195. Ширина
запрещенной зоны в кремнии
=1,1
эВ. Если температуру увеличить от
=300К
до 
=400К,
концентрация электронов в зоне
проводимости увеличится в … раз.
Постоянная Больцмана к=0,86
эВ/K.
Ответ округлить до сотен.
Ответ: 300
(!) 196. Ширина запрещенной зоны в кремнии =1,1 эВ. Если температуру увеличить от =300К до =400К, концентрация дырок в валентной зоне увеличится в … раз. Постоянная Больцмана к=0,86 эВ/K. Ответ округлить до сотен.
Ответ: 300
(!) 197. Температура полупроводника постоянна и меньше температуры истощения примеси. Если концентрацию донорной примеси увеличить в 16 раз, концентрация электронов в зоне проводимости увеличится в … раз.
Ответ: 4
(!) 198. Температура примесного полупроводника постоянна и выше температуры истощения примеси. Если концентрацию донорной примеси увеличить в 8 раз, концентрация электронов в зоне проводимости увеличится в … раз.
Ответ: 8
199. Донорный
уровень фосфора
ниже дна зоны проводимости на 
=0,013
эВ в германии. Концентрация электронов
в зоне проводимости в кремнии n1
в германии-n2.
При Т=10К n2/n1=
,
где x
равно … . Постоянная Больцмана к=0,86
эВ/K.
Ответ округлить до целых.
Ответ: 19
200. Ширина
запрещенной зоны для германия
,
для кремния 
=1,1
эВ. Концентрация электронов в зоне
проводимости для германия n1,
для кремния n2.
При Т=300К отношение n1/n2
равно … . Постоянная Больцмана к=0,86
эВ/К. Ответ округлить до десятков.
Ответ: 1070
(!) 201. При Т=0
химический потенциал собственного
полупроводника
запрещенной
зоны рана … эВ.
Ответ: 1
(!) 202. При Т=0
химический потенциал полупроводника
n-типа
=-0,005
эВ. Донорный уровень расположен ниже
дна зоны проводимости на … эВ.
Ответ: 0,01 – запятая.
(!) 203. Из приведенных величин: m –масса газа, S – энтропия, Т –температура, V –объем, Ω -статистический вес, n –концентрация частиц, p –давление - аддитивными являются:
Ответ: m, S, V.
(!) 204. Изменение
энтропии при переходе из состояния (1)
в состояние (2):
Ответ:
(!) 205. Вероятность Р наступления любого из двух независимых событий А или В равна:
Ответ: сумме вероятностей Р(А)+Р(В)
(!) 206. Вероятность Р одновременного наблюдения 2-х независимых событий А и В равна:
Ответ: произведению вероятностей Р(А)•Р(В)
(!) 207. Неправильным утверждением является. Вероятность случайного события Р:
Ответ: Р изменяется от 0 до ∞
(!) 208. Изменение
энтропии
при
плавлении льда (m-масса, λ -удельная
теплота плавления) равно:
Ответ:
(!) 209. Статический вес системы:
Ответ: зависит от числа частиц системы.
(!) 210. При конденсации пара энтропия системы:
Ответ: уменьшается
(!) 211. Вероятность достоверного события равна … Ответ: 1
(!) 212. Вероятность невозможного события равна… Ответ: 0
(!) 213. Реальные процессы в изолированных системах протекают:
Ответ: в направлении увеличения хаотичности движения частиц в системе
(!) 214. Второе начало термодинамики утверждает, что в замкнутой системе:
Ответ: ΔS≥0
(!) 215. Изменение
энтропии при изотермическом
квазиравновесном процессе
1-2:
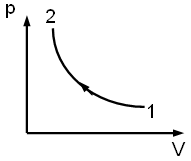
Ответ: ΔS12 = 0
(!) 216. Термодинамическая система находится в равновесном состоянии, если:
Ответ:
217. В замкнутой
системе энтропия может меняться
со временем, как показано на участках:
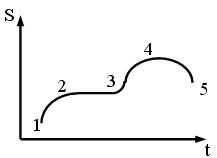
Ответ: 1-2-3
(!) 218. В равновесной
системе
Ответ: 0
(!) 219. Для равновесия двух подсистем замкнутой системы достаточно, чтобы у них были равны только:
Ответ:
(!) 220. Изменение
энтропии
и
для
процессов, изображенных на P-T диаграмме:
Ответ:
(!) 221.
-
соответственно:
статистический вес, энтропия, вероятность
– связаны следующим соотношением:
Ответ:
(!) 222. Необходимым и достаточным условием равновесного состояния системы является:
Ответ: замкнутость системы и стационарность макропараметров
(!) 223. Число доступных микросостояний в некотором фазовом объеме ΔГ:
Ответ: бесконечно для классической частицы, т.к. в каждый момент времени объем, который в фазовом пространстве определяет ее состояние, стремится к нулю
(!) 224. Число
возможных состояний системы из
N =100 квантовых частиц (электронов) в
конечном элементе объема
равно:
Ответ:
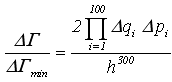
(!) 225. Точка в фазовом пространстве для системы из N частиц характеризует:
Ответ: микросостояние системы
(!) 226. Найдите неправильное утверждение. Фазовое пространство для N независимых частиц можно:
Ответ: представить
как 3N-мерный
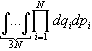интеграл,
где qi={xi
yi
zi},
pi={pxi
pyi
pzi}
(!) 227. Газ из
состояния (1) переходит в состояние (2)
в одном случае по прямой
1-2 , а в другом – по линии 1-3-4-2. При этом
изменение энтропии:
Ответ:
(!) 228.
если:
Ответ: нет правильного ответа
(!) 229.
если:
Ответ: S=const
(!) 230. Энтропия неизолированной системы при необратимом теплообмене:
Ответ: может как и увеличиваться, так и уменьшаться в зависимости от условий
(!) 231. У изолированной системы, находящейся в равновесном состоянии:
Ответ:
(!) 232. При стремлении изолированной системы к равновесному состоянию:
Ответ:
(!) 233. Число
доступных состояний в элементе фазового
пространства
для
классической частицы:
Ответ: → ∞
(!) 234. Для
циклического процесса, изображенного
на рис:
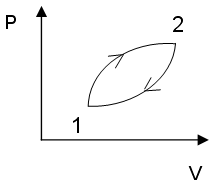
Ответ:
235. На рисунке
приведены графики изохоры, изобары,
изотермы, адиабаты.
Правильные названия графиков:
Ответ: 1-адиабата, 2-изохора, 3-изобара, 4-изотерма
(!) 236. В термодинамической системе при необратимом процессе:
Ответ:
(!) 237. Изменение энтропии идеального газа в результате адиабатного расширения:
Ответ: для однозначного ответа необходимо знать, квазиравновесный процесс или нет
(!) 238. Если F(х) – плотность вероятности случайной величины х, то F(x)dx:
Ответы:
- равно dP(x)
- равно вероятности встретить случайную величину x в интервале от x до x+dx
- принимает значения больше 0, но меньше единицы.
(!) 239. В замкнутой системе при необратимых процессах, если N=const:
Ответ: dE<TdS-pdV
(!) 240. Если х - случайная физическая величина, принимающая ряд дискретных значений х1,х2, … хn, а Рi – вероятность появления хi, то < x2 > равно:
Ответ:
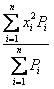
(!) 241. Изображенный
циклический процесс:
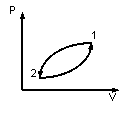
Ответ: необратимый, квазиравновесный
242. Уравнение состояния идеального газа имеет вид:
Ответы:
+
,
+
,
+
,
+
(!) 243. Фазовая траектория для системы из N частиц показывает:
Ответ: изменение микросостояния системы
(!) 244. Размерность статистического веса:
Ответ: безразмерная величина
(!) 245. Изолированный сосуд разделен перегородкой на две половины. В одной находится газ, другая пустая. Перегородку убирают и дожидаются установления равновесия. При этом в системе:
Ответ: энтропия увеличивается, а средняя энергия каждой частицы не изменяется
(!) 246.
Запишите формулу для плотности состояний,
используя шаблон
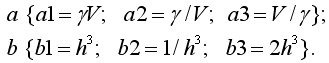
Ответ: a1b2