67. Если - функции распределения по проекциям скоростей для молекул идеального газа, то:

*D)

68. Перейти от классической функции распределения по модулю импульса к функции распределения по модулю скорости f(u):

*B) можно, заменив p на mu и dp на mdu в выражении f(p)dp;

или

Перейти от классической функции распределения по модулю скорости к функции распределения по энергии f(e)

*C) можно, заменив на и du на в выражении f(u)du;

(!) 69. f(x²) – некоторая функция случайной величины x. Интеграл равен: ;

70. Отношение интегралов для молекулы водорода Н₂ (молярная масса водорода 210^-3кг/моль) при Т=300 К с учетом N_A»6×10²³1/моль , где A и B – целые числа, значения которых перечислите через точку с запятой … , … без учета размерностей. (*Ответ: 5; -19)

(!) 71. Отношение максимальных значений функций распределения для молекул идеального газа . При этом отношение наиболее вероятных значений (*Ответ: 4)

(!) 72. Для молекул идеального газа значения интегралов 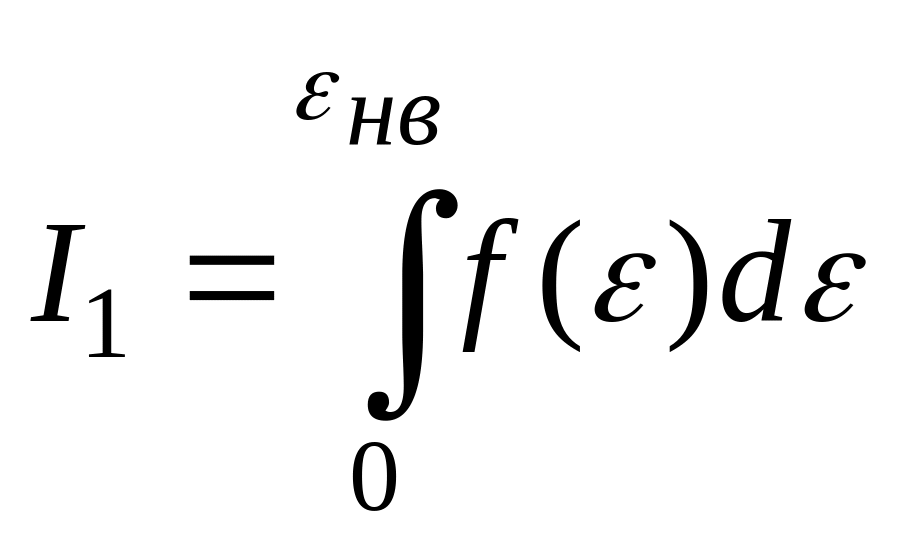и , где - наиболее вероятная энергия:

*B) I₁<I₂;

(!) 73. Для классической функции распределения по модулю скорости при условии

Т=const, а u₂>u₁ отношение ;

*D) >1, если u₁ и u₂ меньше u_нв;

*E) <1, если u₂ и u₁ больше u_нв ;

(!) 74. Для данного газа в равновесном состоянии отношение средней энергии частиц к наиболее вероятной энергии при заданной температуре равно…

(*Ответ: 3)

(!) 75. Если f(u_x) – функция распределения молекул идеального газа по проекции скорости, то для интегралов: , , справедливо следующее соотношение:

*D)

(!) 76. При T=const максимальное значение функции распределения по проекции импульса f(p_x):

*D)~ ;

(!) 77. Значения функций распределения по проекции скорости при , равной наиболее вероятной , для газов с молярными массами и соответственно равны: ; . С учетом T=const отношение (*Ответ: 9)

78. Значения функций распределения по проекции скорости при , равной наиболее вероятной , для одного и того же газа при и соответственно равны ; . Отношение температур для этих функций распределения (*Ответ: 4)

(!) 79. Наиболее вероятное значение проекции скорости для молекул водорода Н₂ при Т=400 К равно … (*Ответ: 0)

80. Для молекулы азота N₂ (молярная масса азота 28 г/моль) наиболее вероятное значение модуля скорости при Т=300 К равна ….м/c. R=8,31 Дж/К×моль. Ответ округлите до десятков. (*Ответ: 420)

81. Для молекулы кислорода О₂ (молярная масса кислорода 32 г/моль) значение средней квадратичной скорости при Т=400 К равна ….. м/c. R=8,31 Дж/К×моль. Ответ округлите до десятков. (*Ответ: 560).

82. Случайная величина х принимает значения от 0 +¥. Функция распределения случайной величины х или плотность вероятности имеет вид , где нормировочный множитель С равен:

*A) b;

(!) 83. Основной постулат квантовой статистики - это ...

*А) принцип тождественности частиц;

(!) 84. Основной постулат квантовой статистики (принцип тождественности) является следствием того, что ...

*А) описание движения отдельной частицы носит вероятностный характер;

(!) 85. Функция распределения по энергии в квантовой статистике – это

*С) среднее число частиц в единичном малом интервале энергии;

(!) 86. Принцип Паули утверждает, что ...

*В) в одном квантовом состоянии может находиться не более одного фермиона

(!) 87. Объем элементарной фазовой ячейки для одной квантовой частицы равен:

Ответ: h³

(!) 88. Одному квантовому состоянию (без учёта спина) соответствует фазовый объём

*В) =

(!) 89. Одному квантовому состоянию для N частиц (без учёта спина) соответствует фазовый объём …

*A) ;

(!) 90. Одному квантовому состоянию для одной частицы в трехмерном пространстве соответствует фазовый объем

*C) ;

(!) 91. Функция распределения Ферми-Дирака по состояниям – это …

*А) среднее число фермионов в одном квантовом состоянии

(!) 92. Функция распределения Ферми-Дирака по состояниям может быть получена, исходя из формулы:

*А) , где вероятность нахождения фермионов в k -том квантовом состоянии

(!) 93. Функция распределения Ферми-Дирака по состояниям находится по формуле , где k – это ...

*В) Набор квантовых чисел, задающих квантовое состояние частицы в атоме;

(!) 94. Функция распределения Ферми-Дирака по энергиям имеет вид …

*B) ;
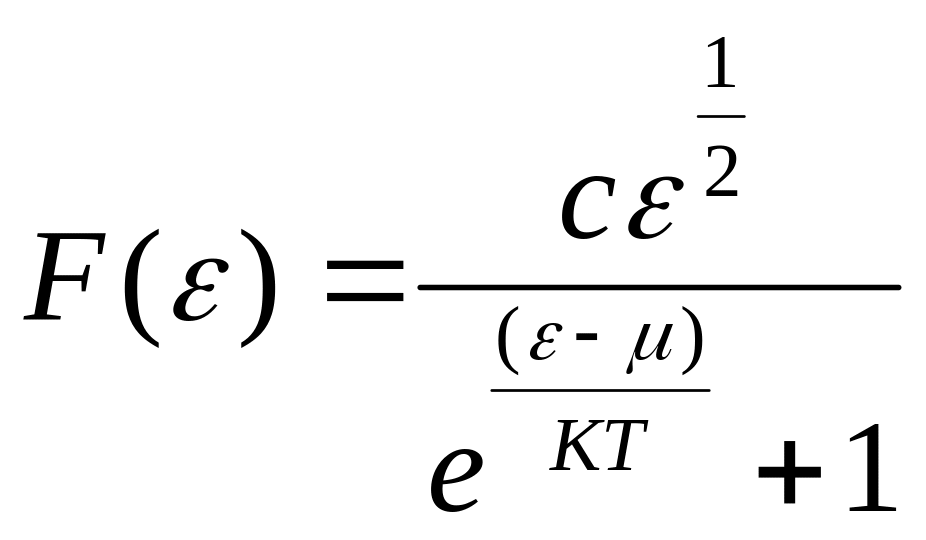