43. Расчет трехфазных цепей при соединении звездой без нулевого провода
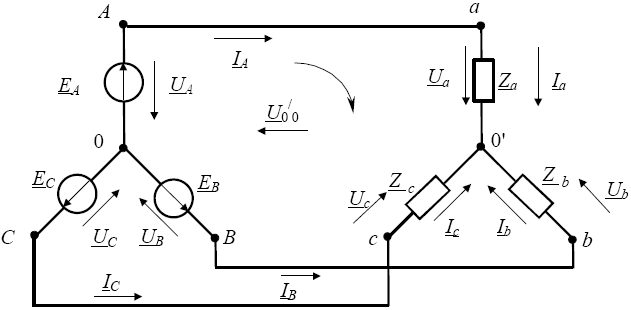
Если цепь симметричная, расчет токов в фазах нагрузки совпадает с расчетом соединения звезда-звезда с нулевым проводом:
IA = Ia = Ua/Za = UA/Za ,
IB = Ib = Ub/Zb = UB/Zb ,
IC = Ic = Uc/Zc = UC/Zc .
Между модулями фазных и линейных токов и напряжений следующие соотношения: Uл=√3Uф, Iл=Iф.
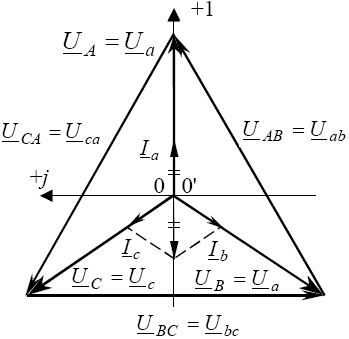
Если цепь несимметричная, напряжение на фазе нагрузки не равно соответствующему напряжению источника. Для определения искомого тока IA=Ia=Ua/Za, IB=Ib=Ub/Zb и IC=Ic=Uc/Zc необходимо отыскать фазное напряжение на нагрузке.
Запишем уравнение 2ого закона Кирхгофа для контуров, образованных источником ЭДС, сопротивлением нагрузки и напряжением холостого хода м/у узлами 0´0: Ua+U00-UA=0, откуда Ua=UA-U00.
Теперь
необходимо определить напряжение
смещения нейтрали:
(если есть
нулевой провод, то:
).
Векторная диаграмма для соединения звезда-звезда без нулевого провода:
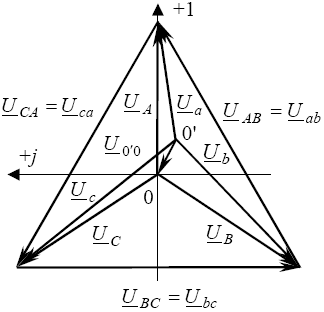
42. Расчет трехфазных цепей при соединении треугольником сим-ой и несим-ой нагрузки.
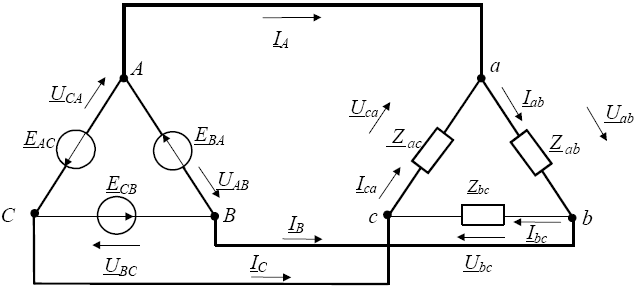
UAB=Uab, UBC=Ubc, UCA=Uca
Фазные токи будут равны:
Iab = Uab/Zab = UAB/Zab ,
Ibc = Ubc/Zbc = UBC/Zbc ,
Iac = Uac/Zac = UAC/Zac .
Линейные токи для несимметричной нагрузки можно определить по первому закону Кирхгофа:
IA = Iab - Ica , IB = Ibc - Iab , IС = Icа - Ibс .
Для симметричной цепи линейные токи в √3 раз больше фазных токов, т.е. Uл=Uф, Iл=√3Iф.
41. Представление периодических функций триг-им рядом. Изменение спектрального состава ряда при симметрии функции относительно оси абсцисс, оси ординат, начала координат.
Любая периодическая несинусоидальная функция может быть представлена в виде ряда Фурье, например:
u(t) = U0 + Um1sin(ωt + Ψu1) + Um2sin(2ωt + Ψu2) + ... + Umksin(kωt + Ψuk), где U0 - постоянная составляющая напряжения; Um1sin(ωt + Ψu1) - основная (первая) гармоника; Umksin(kωt + Ψuk) - высшая (k -я) гармоника; Umk - амплитуда k-й гармоники; Ψk - начальная фаза k-й гармоники; kω - круговая частота k-й гармоники.
В общем случае ряд Фурье содержит бесконечное число членов, но при расчете используют конечное число членов ряда, определяемое точностью расчета.
Для вычисления коэффициентов ряда Фурье целесообразно его члены представить через синусы и косинусы без начальных фаз:
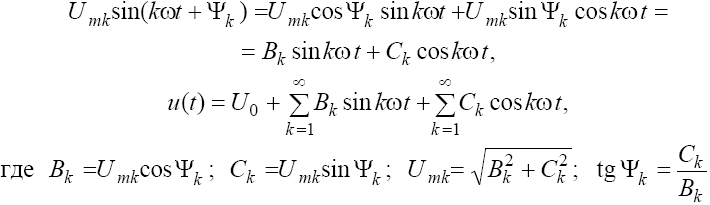
Постоянная составляющая U0 и коэффициенты Bk, Ck могут быть определены из выражений:
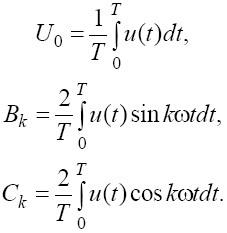
Симметрия относительно оси абсцисс.
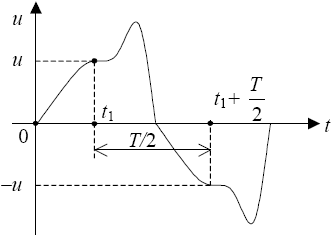
u(t)=-u(t+T/2)
Ряд не содержит четных гармоник
Симметрия относительно оси ординат.
u(t)=u(-t)
Симметрия относительно начала координат.
u(t)=-u(-t)
17. Расскажите о расчете установившегося режима в цепи синусоидального тока с послед-ным соединением r,l,c.
Запишем дифференциальное уравнение по второму закону Кирхгофа для цепи с последовательно соединенными участками R, L,С:
Пусть приложенное к цепи напряжение изменяется
по синусоидальному закону u =Um sin (t + u). Тогда ток в установившемся режиме также будет синусоидальным с такой же частотой i: Im sin (t + i)= Im sin (t + u -). Требуется найти Im и .
Если выбрать начальную фазу тока i =0, то произвольно ориентированная векторная диаграмма повернется на угол i, и вектор тока займет горизонтальное положение, и тогда u =:
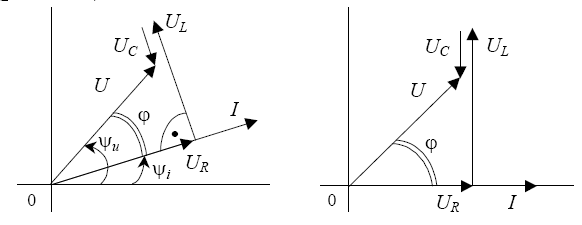
Следовательно,
имеем:
Подставим i и u в исходное уравнение, записанное по второму закону Кирхгофа, и после преобразования получим:
Так как при синусоидальном напряжении ток в цепи должен быть синусоидальным и не может содержать постоянных составляющих, то:
Полученное уравнение справедливо для любого момента времени t, в том числе:
После возведения в квадрат и сложения двух выражений получим связь между амплитудами тока и напряжения:
Полное электрическое сопротивление – параметр пассивного двухполюсника, равный отношению действующего значения электрического напряжения на входе этого двухполюсника к действующему значению электрического тока через двухполюсник при синусоидальных электрическом напряжении и электрическом токе.
Величину (L – 1/C) = X называют реактивным сопротивлением.
Реактивное сопротивление – параметр пассивного двухполюсника, равный квадратному корню из разности квадратов полного и активного электрических сопротивлений двухполюсника, взятому со знаком плюс, если электрический ток отстает по фазе от электрического напряжения, и со знаком минус, если электрический ток опережает по фазе напряжение.