18 Переходные процессы в rl-цепи при гармоническом воздействии

Рассмотрим случай, когда на вход RL-цепи (рис. 4.1,а) подключается гармоническое колебание. Для этого случая принужденная составляющая тока будет

,                                    (4.9)

где         ;                 .

Свободная составляющая тока определятся выражением (4.5).

Постоянную интегрирования А определим исходя из начальных условий, т.е. при t = 0, i = 0, тогда на основании (4.2) запишем

0 = А + Im sin(φu - φ).

Откуда А = -Im sin(φu - φ). Учитывая значение А и выражение (4.9) закон изменения тока в RL-цепи будет иметь вид

.                  (4.10)

Напряжение на индуктивности определяется уравнением , т.е.

,          (4.11)

где        UmL = ImωL.

Из (4.10) видно, что переходной процесс в RL-цепи при подключении ее к гармоническому колебанию, будет протекать по-разному в зависимости от момента включения входного воздействия. Если цепь будет подключена к источнику в момент, когдаφu = φ ± π/2, то в момент включения ток imax = 2Im, т.е. появляется бросок тока. При включении цепи в момент, когда φu = φ в цепи сразу наступает установившийся режим.

Переходной процесс в RL-цепи при ненулевых начальных условиях. Пусть к моменту коммутации ключ К на рис. 4.1,а находился в положении 1 и к RL-цепи было подключено напряжение u(t) = U = const. Следовательно в цепи была запасена энергия магнитного поля WL = LI2 = L(U/R)2. Установим ключ К в положение 2. При этом от цепи будет отключено входное воздействие и индуктивность L будет замкнута на резисторе R. В цепи возникает переходной процесс, описываемый уравнением

iR + Ldi/dt = 0.                                                  (4.12)

Принужденная составляющая тока iпр= 0. Решая уравнение (4.12) с учетом (4.3) - (4.5) находим

.                                          (4.13)

В момент коммутации при t = 0 ток в цепи был i = U/R, поэтому из (4.13) имеем A = U/R. Подставляя полученное значение А в (4.13) будем иметь следующее выражение, описывающее изменение тока в RL-цепи после отключения входного воздействия

.                                                  (4.14)

Напряжение на индуктивности в переходном режиме изменяется по закону

.                                          (4.15)

Графики изменения тока и напряжения изображены на рис. 4.1,в.

Из рисунков и выражений (4.14) и (4.15) видно, что при отключении от индуктивности входного воздействия и замыкании ее на резистор ток и напряжение стремятся к нулю. Это означает, что вся запасенная в индуктивности энергия с течением времени расходуется на тепловые потери в резисторе. Длительность переходного процесса зависит от постоянной времени цепи и переходной процесс заканчивается через времяt ≈ 3τ.

19 Переходные процессы в rс-цепи при ступенчатом воздействии

При расчете переходных процессов в .RC-цепях в качестве независимой переменной выбирают u_c. Затем также составляют дифференциальное уравнение для за­данной RC-цепн, решение которого с учетом начальных условий для и_с(0) и определяет закон изменения напряжения на емкости.

Рассмотрим вначале RС-цепь при нулевых начальных условиях (рис. 6.6), которая подключается в момент t = 0 к источнику по­стоянного u(t) = U или синусоидального u(t) = U_msin((ωt + φ_u) напряжения. Переходный процесс в данной цепи описывается диф­ференциальным уравнением

решение которого ищем также в форме суммы общего и частного решений, определяющих свободную и принужденную составляющие:

 

Свободная составляющая является решением однородного диф­ференциального уравнения

 

 

На рис. 6.7 изображены графические зависимости u_c(t) и i(t).

Анализ   полученных   результатов   показывает,   что   в   момент t = 0₊ емкость С (при нулевых начальных условиях) ведет себя

 

как короткозамкнутый участок. Напротив, при t = ∞ емкость пред­ставляет собой бесконечно большое сопротивление (разрыв цепи для постоянного тока).

Рассмотрим случай гармонического воздействия. Нетрудно ви­деть что при этом

На рис. 6.8 изображен график зависимости u_c(t). Анализ урав­нения (6.31) показывает, что в случае неудачного включения при φ_u = π - φ и большой τ в цепи могут возникать перенапряжения, достигающие на емкости величины ис_тах  ≈2U_mc. В случае удач­ного включения, когда φ_и = π/2 — φ, в цепи сразу наступает уста­новившийся режим.

Ток в цепи

Рассмотрим теперь случай ненулевых начальных условий, когда емкость С, заряженная до напряжения U, разряжается на со­противление R (рис. 6.9). К моменту коммутации в емкости была запасена энергия Wc= С U ²1/2. После коммутации возникает пере­ходный процесс, определяемый уравнением

 

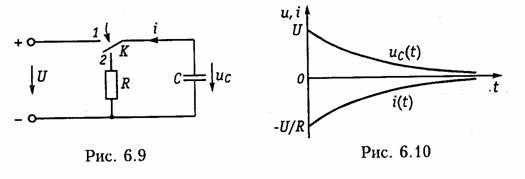
Постоянную интегрирования А находим из начального условия для uc(0₊) = U и

закона коммутации (6.2):

Знак «—» в уравнении (6.36) для тока свидетельствует о том, что ток разряда направлен противоположно опорному направлению напряжения и_с в емкости (см. § 1.2). На рис. 6.10 приведены гра­фики изменения напряжения и_с(t) и тока i(t) данной .RC-цепи. Следует подчеркнуть, что вся запасенная энергия We емкости с течением времени преобразуется в элементе R в тепло. При нену­левых начальных условиях С ведет себя как источник напряжения.