1. Предел функции в точке. Единственность предела. Ограниченность функции, имеющей предел.

Число А называется пределом функции f в точке а, если она определена на некоторой окрестности а, т.е. на некотором интервале (c,d), где c<a<d, за исключением, быть может, самой точки а, и если для всякого >0 можно указать зависящее от него >0 такое, что для всех x, для которых 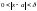имеет место неравенство 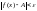. Тот факт, что А есть предел f в точке a, принято записывать 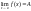или .

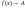
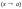Теорема. Если 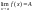, где A – конечное число, то на некоторой окрестности U(a) функция f(x) ограничена, т.е. существует положительное число М такое, что 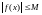для всех ,.

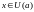Доказательство. Из условия теоремы следует существование окрестности U(a), такой, что 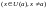. Отсюда для указанных х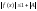 , где надо считать .

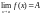2Бесконечно малые функции.Теорема о связи функции её предела и бесконечно малой.Свойства бмф.

Св-ва б.м.ф.:

1) Если функция f(x) ограничена, а m(x) бесконечно большая, то

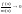
2) Если абсолютная величина f(x) ограничена снизу положительным числом, а m(x) не равная нулю бесконечно мала, то

Теорема.Если функция f(x) имеем предел,равный А,то её можно представить как сумму числа А и бесконечно малой функции α(x),т.е если 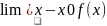=A,то f(x)=A+α(x).

Теорема (обратная).Если функцию f(x) можно представить в виде суммы числа А и бесконечно малой функции α(x) ,то число А является пределом функции f(x),т.е если f(x)=А+α(x),то =A.

Предел суммы равен сумме пределов: .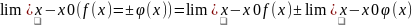

Предел произведения равен произведению пределов

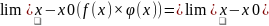
Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

Теорема. Если элементы сходящейся последовательности {xn}, начиная с некоторого номера, удовлетворяют неравенству xn ≥ b (xn ≤ b), то и предел a этой последовательности удовлетворяет неравенству a ≥ b (a ≤ b).

Доказательство. Пусть все элементы xn, по крайней мере начиная с некоторого номера, удовлетворяют неравенству xn ≥ b. Требуется доказать неравенство a ≥ b. Предположим, что a < b. Поскольку a - предел последовательности {xn}, то для положительного ε = b - a можно указать номер N такой, что при n ≥ N выполняется неравенство |xn - a| < b - a. Это неравенство эквивалентно следующим двум неравенствам: -(b - a) < xn - a < b - a. Используя правое из этих неравенств, получим xn < b, а это противоречит условию теоремы. Случай xn ≤ b

рассматривается аналогично. Теорема доказана.

3 Непрерывность функции в точке.

Функция f(x) называется непрерывной в точке х₀, если она определена в некоторой окрестности этой точки, в том числе в самой точке х₀, и если её приращение в этой точке, соответствующее приращению аргумента 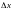, стремится к нулю при : .

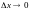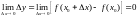КОРОЧЕ: 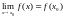. Непрерывность основных элементарных функциий

Теорема. Сумма, произведение и частное двух непрерывных функций есть функция непрерывная

Теорема. Пусть функции u=φ(х) непрерывна в точке х0, а функция у=ƒ(u) непрерывна в точке u0=φ(хо). Тогда сложная функция ƒ(φ(х)), состоящая из непрерывных, функций, непрерывна в точке х0. ТеоремаЕсли функция у=ƒ(х) непрерывна и строго монотонна на [a;b] оси (Oх, то обратная функция у=φ(х) также непрерывна и монотонна на соответствующем отрезке [c;d] оси Оу. все основные элементарные функции непрерывны при всех значениях х, для которых они определены. Теорема о переходе к пределу под знаком непрерывной функции.

Пусть ф-я y=f(x) непрерывна в x0. Это означает, что существует lim (x->x0) f(x) = p(x0). Пусть существует функция y=f(y) - непрерывная в y0 => p(x0)(lim(y->y0) f(y)) = f(y0). Тогда сложная функция y=f(p(x)) будет непрерывна в точке х, т.е предел сложной функции lim (x->x0) f[p(x)]=f(p(x0)]=f [lim (x->x0 p(x)]. Операция взятия предела и операция взятия непрерывности функции перестановочны между собой Теорема о непрерывности сложной функции.

Пусть x = j(t) непрерывна в точке t0, а функция f(x) непрерывна в точке x0 = j(t0). Тогда функция y = f(j(t)) непрерывна в точке t0.

Билет 4 Замечательные пределы

Первый замечательный предел

Предел Отношения синуса к его аргументу равен единице,когда аргумент стремится к нулю. Второй замечательный предел

Эквивалентные б.м.ф. Таблица эквивалентных б.м.

Эквивалентными (асимптотически равными) называют функции j(x) и y(x) (обе стремящиеся к нулю), если выполняется свойство .

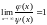Теорема Предел отношения двух бесконечно малых функций не изменится,если каждую или одну из них заменить эквивалентной ей бесконечно малой.

Билет 5

Если функции j(x )и y(x), участвующие в 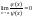, суть бесконечно малые при 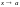, то j(x) при 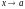есть бесконечно малая высшего порядка по отношению к (бесконечно малой) y(x) (если же это были бесконечно большие, то j(x) более низкого порядка, чем y(x).

Теорема о связи ббф и бмф. Пусть функция f(x)-бб при . Тогда функция a(x) –бм при

Доказательство (?). 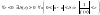Бесконечно большая функция.

Функция называется бесконечно большой при х-а, где а – число или одна из величин , ∞+∞ или , если , где А – число или одна из величин, или .

Связь бесконечно больших и бесконечно малых функций осуществляется в соответствии со следующей теоремой.

Теорема. Если f(x)-0 при х-а (если х-∞ ) и не обращается в ноль, то

Билет 6 Односторонние пределы. Классификация точек разрыва.

Число А называется пределом функции f(x) в точке x=a справа (при +0), если .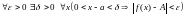

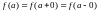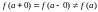Точки, в которых функция f(x) не является непрерывной, называются точками разрыва для функции f(x). Если в точке x=a существуют пределы f(a+0), f(a–0), но неравенство не выполняется, то точка х=а называется точкой разрыва первого рода для функции f(x). Причём, если , то точка x=a называется точкой устранимого разрыва для функции f(x). Если же в точке x=a у функции f(x) не существует правого или левого предела или же эти пределы бесконечны, то функция f(x) имеет в точке x=a разрыв второго рода.

Предел в бесконечности.Число А называется пределом функции к бесконечности если для любого положительного числа есущ такое число М=М(е)>0,что при всех x ,удовлетворяющих неравенству │Х│>М выполняется неравенство │f(x)-A│<e

Геометрический смысл

Для ¥е> 0 э м>0,что при Х €(-∞;-М) или (М,+∞) соответствующие значения функции f(x) попадают в е-окрестность точки А,т.е точки графика лежат в полосе шириной 2е,ограниченной прямыми y=A+e и y=A-e

7.билетПроизводная. Геометрический и механический смысл производной. Уравнение касательной и нормали к графику функции.

П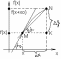 роизводной функции f(x) в точке x называется предел её приращения 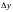в этой точке к соответствующему приращению аргумента , когда стремиться к нулю (при условии, что этот предел существует). Для обозначения производной используют символы 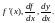Определение записывается и таким образом .

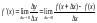Геометрический смысл производной заключается в том, что есть tg угла наклона касательной, проведенной в точке x₀. KN=Dy, MK=Dx

tg угла KMN=Dy/Dx

вычислим предел левой и правой части:

limtga=lim(Dy/Dx) Dx®0

tga₀=y`

a®a₀

При Dx®0 секущая MN®занять положение касательной в точке M(tga₀=y`, a®a₀).

Касательной Т к кривой y=f(x), проходящей через точку (x;f(x)), называется предельное положение секущей при Dx®0. Уравнение касательной в точке M(x₀,f(x₀)) записывается в виде .

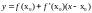Нормалью к графику функции в точке M(x₀,f(x₀)) назовём прямую, проходящую через точку М и перпендикулярную касательной, проходящей через эту же точку.

8билет Дифференцируемость функции. Дифференциал. Необходимое и достаточное условие дифференцируемости. Геометрический смысл дифференциала.

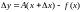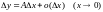Функция f(x) называется дифференцируемой в точке х, если её приращение в этой точке может быть представлено в виде , где величина А не зависит от Dx.

Теорема. Для того, чтобы функция f(x) была дифференцируемой в точке х, необходимо и достаточно, чтобы она имела в этой точке конечную производную. Тогда величина А из равна производной: A=f’(x).

Достаточность. Из существования производной выводим дифференцируемость