2 0. Залежність кінцевого значення різниці населеностей лазерного переходу

(1) де Ці два рівняння діють саме в період часу Δt. Імпульс досягає максимуму, коли Імпульс спадає до нуля, коли ; імпульс спадає до нуля, коли , потім Δn наростає до порогового значення. Якщо знову зменшити добротність, то процес повториться.

Якщо підставити k і kвт в друге рівняння системи (1) отримаємо:

тепер поділимо його на перше рівняння:

, або про інтегруємо в інтервалі з проміжка Δt: (t1,t2)є Δt Виберемо в якості t1, t2 – границі проміжку Δt. Тоді інтеграл стає рівним нулю і ми маємо При будь-яких Δnкін/Δnпор, Δnкін<Δn0 і крім того Δnкін < Δnпор.

- яскравість;

- коефіцієнт Ейнштейна для вимушеного переходу;

- густина енергії зовнішнього поля;

-яскравість через одну з сторін резонатора;

к – коефіцієнт підсилення;

- ступінь виродження;

- сечение перехода;

- число півхвиль (хвиль) для лінійного (круглого) резонатору

21. Потужність генерації лазера при миттєвому перемиканні добротності резонатора.

При миттєвому перемиканні добротності(МПД) виникає гігантський імпульс, обумовлений тим, що ми уникаємо наростання поля в резонаторі(внаслідок МПД), і тоді в активному середовищі запасається велика інверсна населеність, яка перевищує пороговий рівень. В результаті виникає суттєве перевищення підсилення в лазері над втратами і випромінюється короткий і потужний імпульс.

З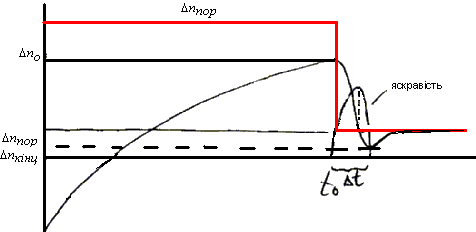 апишемо систему з 2 р-нянь, яка характеризує дворівневу систему (маємо зміну в часі яскравості і різниці населеності): 1) - зміна яскравості по закону Бугера, та 2) . Маємо справу з усередненими значеннями, тому „-” не пишемо для спрощення. Вони починають діяти з моменту , бо добротність генерації змінюється з високої на низьку. Імпульс досягає максимуму, коли , імпульс спадає до 0 коли , потім наростає до порогового значення. Якщо знову змінити добротність, то процес повториться. , бо , та . Поділимо р-ня 1) на 2) і підставимо . Проінтегруємо в інтервалі з проміжка : . Виберемо в якості границі проміжку . Тоді і або . При , Намалювали такий графік , і виходить, що він лежить нище графіка , тому : .

, коли ,(тоді ). Щоб знайти треба час, коли . Отже

22. Енергія генерації лазера при миттєвому перемиканні добротності резонатора.

Т ут можно піти 2 шляхами: 1) (Пугач) Ітак є в нас перехід чатинки з рівня до рівня : тобто . , тобто зміна населеності рівнів =2 {в знаменнику}. Ще раз при кожному переході населеність одного і другого рівня змінюється на 1, тобто різниця населеностей з кожним переходом змінюється на 2. Тоді (2-тому, що перехід одного електрона змінює на 2) 2) (Хижняк) (Для фанатов! Нам такого не давали) Більш строго . отримай з попереднього білета узявши такий інтеграл . А далі біс його зна.

2 3. Тривалість імпульсу генерації лазера при миттєвому перемиканні добротності резонатора.

Гігантський імпульс(ГІ) асиметричний. Його передній фронт крутіший заднього. Оцінка тривалості ГІ , як відношення його енергії до пікової потужності, дозволяє визначити нижню межу. Визначають по напівширині: .

Дослідемо вираз: таке значення , коли мінімальне (перший графік): Від цього значення будемо рухатись до 0 (по вісі ) , тоді добротність буде великою, яскравість дуже швидко досягне свого максимального значення. Тоді буде передній фронт буде короткий, але спад імпульсу повільний(через Q) (резонатор «дзвонить»). При імпульс би весь час був в резонаторі( ). При від мінімального значення добротність резонатору буде низькою, великі втрати, тому імпульс наростає повільно, але швидко обривається(внаслідок великих втрат). Буде довгий фронт і короткій хвіст. При - стаціонарна генерація(нескінченно довга).