
- •1.Типы переходов квантовых частичек между энергетическими уровнями, вероятности переходов и взаимосвязь между ними.
- •2.Взаємодія поля і речовини. Спонтанні і вимушені переходи.
- •4. Напівкласичний метод аналізу в квантовій радіофізиці.
- •5. Одержання інверсії в дворівневій системі.
- •6. Інверсія в трирівневій системі в нвч-діапазоні. Пушпульна схема інверсії.
- •7. Інверсія в трирівневій системі оптичного діапазону на переході 2-1.
- •9. Стаціонарне підсилення в активній речовині.
- •10. Конструкції квантових парамагнітних підсилювачів резонаторного і хвильоводного типів.
- •11. Залежність ненасиченого коефіцієнту підсилення на переході 2-1 трирівневої схеми оптичного діапазону від потужності накачки.
- •12. Залежність ненасиченого коефіцієнту підсилення на переході 3-2 трирівневої схеми оптичного діапазону від потужності накачки.
- •13. Коефіцієнт нелінійності активної речовини для трьохрівневої системи на переході 2-1.
- •14.Умови стаціонарної генерації лазера і залежність потужності генерації від параметрів резонатора.
- •15.Залежність потужності стаціонарної генерації лазера від потужності накачки.
- •16.Енерговиділення в каналах трирівневої схеми лазера при відсутності генерації.
- •17.Енерговиділення в каналах трирівневої схеми лазера при стаціонарній генерації.
- •18. Система рівнянь для нестаціонарної генерації лазера.
- •19.Способи швидкого перемикання добротності резонатора лазера і
- •2 0. Залежність кінцевого значення різниці населеностей лазерного переходу
- •21. Потужність генерації лазера при миттєвому перемиканні добротності резонатора.
- •22. Енергія генерації лазера при миттєвому перемиканні добротності резонатора.
- •2 3. Тривалість імпульсу генерації лазера при миттєвому перемиканні добротності резонатора.
- •24 Розподіл поля типів коливань (мод) оптичного резонатора?
- •25 Метод Фокса Лі для аналізу характеристик мод лазерного резонатора.
- •26 Частотний спектр повздовжніх і поперечних типів коливань лазерних резонаторів
- •27. Втрати мод в резонаторі лазера.
- •33. Однорідне і неоднорідне уширення лінії підсилення активної речовини лазера. Провали беннета.
- •35. Залежності потужності генерації лазера від частоти при різних уширеннях лінії підсилення активної речовини. Провал лемба.
- •36.Квантове підсилення імпульсного сигналу (нестаціонарне підсилення).
- •37. Матриці Джонса для анізотропних оптичних елементів і систем з анізотропних елементів.
1.Типы переходов квантовых частичек между энергетическими уровнями, вероятности переходов и взаимосвязь между ними.
Типы переходв квантовых частичек между энергетическими уровнями делятся на две группы: излучательные переходы и поглощение. Каждая из них включает в себя два типа переходов между энергетическими уровнями: вынужденные и спонтанные. Как известно, описание квантовомеханических систем является вероятностным, т.е. существуют вероятности перехода с одного энергетического уровня на другой в еденицу времени. Велечины, которые описывают вероятности вынужденных и спонтанных переходов между энергетическими уровнями называются коэфициэнтами Эйнштейна, и были введены им задолго до завершения квантовой теории. Спонтанному излучнию соответствует матрица {Anm}, индексы которой указывают с какого (n) на какой (m) уровень происходит переход, причем за нулевой уровень принимается ниаболее низкая возможная энергия атома. Вынужденному излучению соответствует матрица {Bnm}. Размерность элементов этих матриц – [1/сек]. Матрицы {Anm} и {Bnm} симетричны только в том случае, если кратности вырождения всех енергитеческих уровней системы одинаковы (и как правило равны еденице). Связь между коэфициэнтами матриц {Anm} и {Bnm} задается соотношением:
 (1)
(1)
Здесь,
![]() -
кратности вырождения соответствующих
уровней (число различных состояний
системы на определенном уровне энергии),
- частота энергетического перехода
между уровнями.
-
кратности вырождения соответствующих
уровней (число различных состояний
системы на определенном уровне энергии),
- частота энергетического перехода
между уровнями.
С учетом второго постулата Н.Бора, (1) можно переписать следующим образом:
 (2)
(2)
Из формулы (2) можно сделать (фундаментальное) заключение, о том, что вероятность спонтанного перехода сильно возростает с ростом энергии этого перехода. Это сильно сказывается в оптическом диапазоне, и как следствие – мазеры опередили создание лазера почти на 10 лет.
Вероятность
спонтанного перехода по определению
связана со средним временем жизни на
данном переходе:
![]() .
А среднее время жизни, в свою очередь,
связано соотношением неопределенностей
с шириной линии излучения (поглощения)
атома на данном переходе (это правда
уже другая тема).
.
А среднее время жизни, в свою очередь,
связано соотношением неопределенностей
с шириной линии излучения (поглощения)
атома на данном переходе (это правда
уже другая тема).
Вобщем, спонтанные и вынужденные переходы – не единственные возможные – но они основные. Еще бывают квадрупольные (спонтанные и вынужденные мы рассматривали в дипольном приближении), иагнитные, безизлучательные. Последние также имеют фундаментальное значение (помним это 3-х 4-х уровневым схемам), их задают матрицей {Snm}. Таким образом, полная вероятность квантовых переходов с уровня n на m может быть предтавлена как:
![]() (3)
(3)
Из
последнего уровнения можно оценить
среднее время жизни на n-м
уровне в данной квантовой системе:
![]() .
.
2.Взаємодія поля і речовини. Спонтанні і вимушені переходи.
В
лазерах іде взаємодія випромінювання
і речовини. Речовина
характеризується
населенностями
![]() на
двох рівнях.
на
двох рівнях.
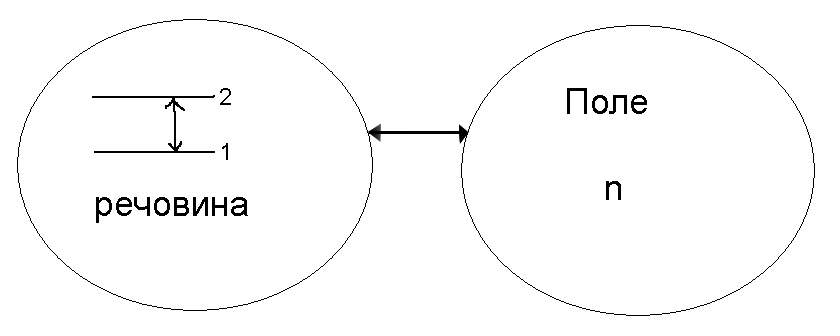
Уточнення:
- не вироджені рівні (населеності на один ступінь виродження)
n – к-ть квантів, що є в одній моді
В
полі випромінювання є набір фотонів n.
Існує ймовірність ![]() що кількість n
збільшиться
на 1.
що кількість n
збільшиться
на 1.
![]() ,
K
– деякий
коеф.
,
K
– деякий
коеф.
![]()
![]()
Тут
перший доданок – імовірність вимушеного
випромінювання ![]() випромін.;
випромін.;
![]() поглинання.
поглинання.
![]() – йм.
вимуш. переходу
– йм.
вимуш. переходу
Другий
доданок – спонтанне випромінювання
(![]() - число переходів).
- число переходів).
![]() - йм. спонтанного переходу.
- йм. спонтанного переходу.
Треба
пам’ятати, що ![]() - скільки частинок припадає на од. об’єму
на одиничну полосу частот і кожна з цих
населеностей це на 1 ступінь виродження.
- скільки частинок припадає на од. об’єму
на одиничну полосу частот і кожна з цих
населеностей це на 1 ступінь виродження.
В речовині існують випромінювальні процеси (спонтанні і вимушені_ ті безвипромінювальні (зміни стану речовини не в результаті взаємод. з полем фотонами, а з фононами)

![]() - ім-ть
того, що част. Переходить в од. часу з
і-того
на j-тий
рівень.
- ім-ть
того, що част. Переходить в од. часу з
і-того
на j-тий
рівень.
![]() спонтанні
(під дією нульових коливань вакууму). А
– коеф. Енштейна.
спонтанні
(під дією нульових коливань вакууму). А
– коеф. Енштейна.
![]() коеф.
Енштейна для вимуш. переходів
коеф.
Енштейна для вимуш. переходів
![]() –
густина
поля
–
густина
поля
![]() – релаксаційні
процеси
– релаксаційні
процеси
![]()
![]() ,
,
![]() - без зовн поля
- без зовн поля
![]() =>
=> ![]() внутр.
Поле, що завжди існує в речовині.
внутр.
Поле, що завжди існує в речовині.
 - ф-ла
Планка - густина поля яке припадає на
од. об’єму і на од. полосу частот.
- ф-ла
Планка - густина поля яке припадає на
од. об’єму і на од. полосу частот.
Вимуш. процеси пояснив Енштейн:
![]() - к-ть коливань (число мод), що припадає
на одиничну полосу частот в одиницю
часу.
- к-ть коливань (число мод), що припадає
на одиничну полосу частот в одиницю
часу.
 - к-ть фотонів на одну моду
- к-ть фотонів на одну моду
![]() - ен фотону.
- ен фотону.
 - в
термадинам. рівновазі
- в
термадинам. рівновазі
![]() - ступінь виродження і-того
рівня
- ступінь виродження і-того
рівня
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Висновки:
вимушені процеси є тільки тоді, коли

спонтанні процеси – сильно залежать за частотою (тому в оптиці спонтанними переходами можна знехтувати)
3. Вероятностный метод анализа в квантовой радиофизике.
Вероятностный метод анализа в кв.р/ф – это метод описания квантовых систем с токи зрения вероятностностей переходов между энергетическими уровнями. Он основан на составлении и решении системы балансных уровнений, которая является следствием закона сохранения полной энергии квантовой системы, и закон Буггера, который описывает изменение яркости электромагнитного излучения в зависимости от углубления в эту среду. Вероятностный метод анализа квантовой стстемы позволяет с хорошей точностью описывать движение энергии в системе, и решает такие задачи: накачка вещества в стационарном режиме; определение типов коебаний лазерного излучения вдоль продольной оси резонатора аксиальных мод; вычисление ширины линии излучения; получение условий, определяющих генерацию; динамику генерации гиганского импульса; устойчивость стационарного режима, т.д.
ЗДЕСЬ НАПИСАНО ПОЛНОЕ ГОНИВО, С ТОЧКИ ЗРЕНИЯ КОНСПЕКТА, Т.К. ЕГО КТО-ТО ЗАБИЛ ОТСКАНИТЬ!!!!!! ВСЯ ИНФА НАБИТА ПО КНИЖКАМ, ПОЭТОМУ ФИЗИКА КОНЕЧНО ТА ЖЕ, НО ОБОЗНАЧЕНИЯ… ДОПУЩЕНИЯ И ФОРМЫ В ФОРМУЛАХ МОГУТ СИЛЬНО ОТЛИЧАТЬСЯ ОТ ЛЕКЦИЙ.
Система балансных уравнений имеет вид:
![]() (1)
(1)
Здесь:
![]() ,
где {Aji}
– матрица вероятности спонтанных
переходов; {Sji}
– матрица вероятности беизлучательных
переходов; {Bji}
– матрица вероятности вынежденных
переходов; {
,
где {Aji}
– матрица вероятности спонтанных
переходов; {Sji}
– матрица вероятности беизлучательных
переходов; {Bji}
– матрица вероятности вынежденных
переходов; {![]() }
– густоты излучения на данной частоте
перехода j
-> i
или I
-> j,
следовательно:
}
– густоты излучения на данной частоте
перехода j
-> i
или I
-> j,
следовательно:
![]() .
{Pji}
– полная вероятность перехода на уровень
i
с уровня j,
.
{Pji}
– полная вероятность перехода на уровень
i
с уровня j,![]() - концентрация электронов на i-м
энергетическом уровне. Решение системы
линейных уровнений (1) позволяет найти
средние концентрации на всех энергитических
уровнях системы, и следовательно, в
первом приближении оценить например
условие инверсии среды. Ясно, что перед
тем как решать эту систему, надо
определить, какими коэфициэнтами матрицы
{Pji}
можно пренебречь, а какие долны сильно
влиять на ее решение. Указания примерно
такие существуют только те переходы,
которые учитываются в схеме (двох-, трех-
или 4-х уровневой системы), впрочем там
все как правило нарисованно, поэтому
на этом не будем останавливаться.
- концентрация электронов на i-м
энергетическом уровне. Решение системы
линейных уровнений (1) позволяет найти
средние концентрации на всех энергитических
уровнях системы, и следовательно, в
первом приближении оценить например
условие инверсии среды. Ясно, что перед
тем как решать эту систему, надо
определить, какими коэфициэнтами матрицы
{Pji}
можно пренебречь, а какие долны сильно
влиять на ее решение. Указания примерно
такие существуют только те переходы,
которые учитываются в схеме (двох-, трех-
или 4-х уровневой системы), впрочем там
все как правило нарисованно, поэтому
на этом не будем останавливаться.
Из решения системы балансных уравнений можно найти коэфициэнт усиления по такой формуле:

Закон буггера:
![]() (2)
(2)
Здесь, S – яркость [Вт/см2], - коэфициэнт нерезонансных потерь, k – коэфициэнт резонансных взаимодействий (или, для линии генерации – коэфициэнт усиления, для линии накачки – коэф. поглощения (накачки)).
Закон Буггера дает нам возможность рассчитать граничную яркость генерации, например в случае трехуровневой системы имеем:
 (3)
(3)
(3) можно переписать в виде:
 (4)
(4)
Дальше уже ясно: подставляем (4) в (2), решаем дифур, и получаем много всего интересного
