2.5. Задача Эйлера.

Леонард Эйлер – великий математик, родившейся в Швейцарии, но проживающий в Санкт-Петербурге.

Н ачнем с детской задачи.

Нарисовать фигуру, не повторяя линии дважды.

Сформулируем её на языке теории графов: дан неориентированный граф. Требуется построить цепь, проходящую через все ребра ровно 1 раз (такая цепь называется Эйлерова).

Аналогично – задача построение Эйлерового цикла.

Задача Эйлера и состоит в том, чтобы выяснить, обладает ли данный граф Эйлеровой цепью или Эйлеровым циклом.

Как Эйлер пришел к этой задаче?

Задача о 7 мостах.

В городе Кенигсберг течет река, через которую проложено 7 мостов. Можно ли обойти все мосты ровно по 1 разу.

Видим, что и эта и та задачаиз теории графов.

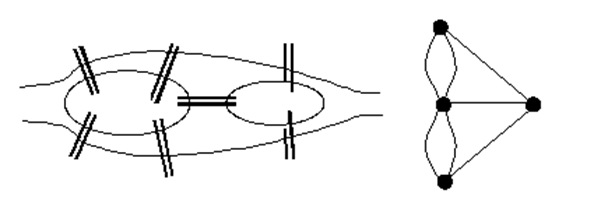
Получим новый вид графа: так называемый мульти граф. В котором вершины могут быть соединены нескольким ребрами. Задача Эйлера имеет смысл и для мульти графа.

Эйлер решил эту задачу, введя простое понятие.

Степень вершин графа – это количество ребер, из нее исходящих (ей инцидентных).

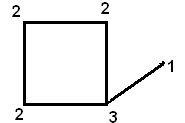
- Степени вершин.

Теорема (Эйлера).

1)Связный граф обладает незамкнутой Эйлеровой цепью  ровно 2 его вершины имеют нечетную степь.

2) Связный граф имеет, обладает незамкнутым Эйлеровым циклом  все его вершины имеют четную степень.

Идея доказательства:

1)Пусть построена Эйлерова цепь

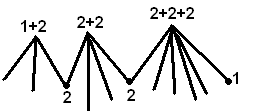
Видим, что 1 вершины нечетной степени – это начало и конец

Эйлеровой цепи.

2) Так как теперь начальная конечная вершины совпадают, то и вместе – четная.

Для небольших графов мы не нуждаемся в алгоритме, для больших – алгоритм прост.

П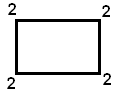 римеры.

1)Все вершины имеют четную степень, по теореме графов обладают Эйлеровым ц циклом. Начинать можно из любой вершины.

2)Видим 2 вершины нечетной степени, по теореме граф обладает незамкнутой 00 Эйнеровой цепью. В одной из них надо начинать, в другой заканчивать. Мы 0 1 построили незамкнутую Эйлерову цепь.

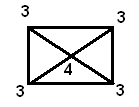
3) Имеем 4 вершины нечетной степени, по теореме графо не обладает ни Эй Эйлеровой цепью, ни Эйлеровым циклом.

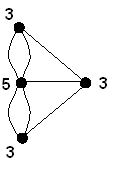
То же самое- обойти 7 мостов невозможно.

2 .6. Плоские графы и формула Эйлера.

Всякую ли фигуру можно «распутать»?

Опр. Граф называется плоским, если он расположен на плоскости и его ребра не пересекаются (кроме как в вершинах). Видим, что неплоский граф превратился в плоский. Поэтому определение не вполне корректное.

Поэтому усилим определение и дадим новое.

Опр. Граф называется планарным, если его можно расположить на плоскости так, что ребра не будут пересекаться.

Видим, что первоначальный граф был планарным.

Возникла проблема планарности: всякий ли неориентированный граф планарен (можно ли его распутать)

Ч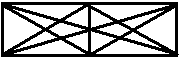 тобы решить эту сложную проблему(выяснить,какие графы планарные, а какие нет), мы сначала изучим свойства планарных графов.

Формула Эйлера.

Для плоских графов введем новое понятие.

Опр. Грань плоского графа – часть плоскости, ограниченная его ребрами и не содержащая в себе ни ребер, ни вершин.

4 – в число граней всегда включают бесконечную грань.

Обозначим число граней плоского графа через Г. Также обозначается число его вершин В, чисор ребер Р.

Связаны ли между собой числа В,Г,Р?

Попробуем нащупать эту связь на практике.

1 пример. Уже нарисован.

Г=4; В=2; Р=6

2 пример

Г=2; В=4; Р=4

3 пример

Г=3; В=5; Р=6

Видим, что во всех 3 случаях В+Г-Р=2

Эйлер доказал, что это формула всегда верна.

Теорема(формула Эйлера)

Для любого плоского связного графа В+Г-Р=2.

Доказать ее в общем случае совсем не просто.

Замечание 1: Если плоский граф не связан, а состоит из k компонентов связности, то формула Эйлера усложняется

В+Г-Р=К+1

Замечание 2: Оказывается, формула Эйлера верна не только для плоских графов, но и для многогранников в пространстве. Дело в том, что любой многогранник можно превратить в плоский связанный граф (т.е. он планарен), растянув одну из его граней и спроецировав на плоскость.

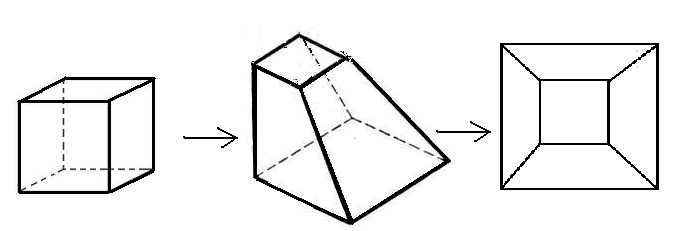
Ясно, что В и Р при этом не меняется, а число граней вроде бы меняется,: исчезает растянутая грань, но добавляется бесконечная. Значит, число Г так же не меняется, и формула Эйлера верна.

Замечание 3: Выразим из формулы Эйлера число граней

В-Р+Г=2 => Г=2-В+Р

Э то позволяет для любого планарного графа заранее предсказать число граней, которое получится после его распутывания.

Пример: Дан планарный граф.

Предскажем число Г. Г=2+Р-2=2+11-6=7 граней

Р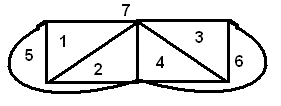 аспутаем граф и проверим.

Формула Эйлера – единственное равенство, верное для всех плоских графов. Но есть еще 2 равенства.

Теорема.

1)Для любого плоского связного графа (кроме 2 исключений и ) верно неравенство

2Р≥ЗГ

2)Если к тому же среди значений нет ни одного треугольника. То неравенство усиливается.

2Р≥4Г

С одной стороны каждое ребро ограничивает не более 2 граней.

Значит

Г≤2Р

С другой стороны, каждая грань ограничена не меньше чем 3 ребрами(кроме 3 исключений )

Поэтому Р≥3Г

Из 2 неравенств следует 2Р≥ЗГ

Из 3 исключений неравенство случайно верно для графа Р=2, Г=1 (2*2>3*1). А 2 других так и остаются исключениями.

2)Если среди граней нет ни одного треугольника, то вместо Р≥3Г можем записать Р≥4Г.

Соответственно 2Р≥4Г.

Теперь можно доказать не планарность 2 исторически первых графов.

Граф № 1. (полный граф с 5 вершинами)

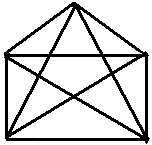
Граф № 2. (задача про 3 дома и 3 колодца)

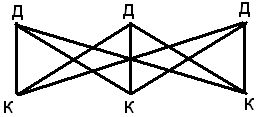
Теорема: Графы № 1 и №2 не планарные.

Доказательство.

1)Допустим, что граф № 1 планарен. Тогда модем заранее предсказать число его граней Г.

В=5; Р=10 => Г=2+10-5=7

Подставим в неравенство

2Р≥3Г. Получим 20≥21 – неверно. Противоречием, граф не планарен.

2) Докажим,граф №2 планарен.

В=6; Р=9

Значит Г=2+Р-В=2+9-6=5

2Р≥3Г =. 18≥15 верно.

Н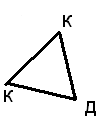 о заметим, что среди граней не может быть ни одного треугольника.

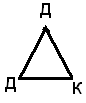
- невозможно - невозможно

Четырехугольники теоритически могут быть.

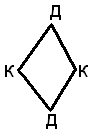
Поэтому неравенство усиливается 2Р≥4Г => 18≥20 - неверно. Противоречием, граф №2 не планарен. (чтд)

Теперь можем получить бесконечно много не планарных графов. Во-первых, можем добавлять на ребрах графов №1 и №2 любое число новых вершин.

Они, конечно, тоже непоанарны: если бы удалось их распутать, мы бы убрали добавленные вершины и заодно распутали бы графы №1 и № 2, что невозможно.

Во-вторых, можем добавлять к графам типа 1 и 2 новые ребра.

Построить принципиально новый не планарный граф никак не удавалось, пока не было доказано, что их не существует.

Теорема. Куратовского-Понтрягина.

Граф планарен  он не содержит в себе графов типа 1 и 2.

Понятие о толщине графа.

Если граф не планарен, то разместить его в плоскости нельзя. Но можно разместить его в нескольких плоскостях.

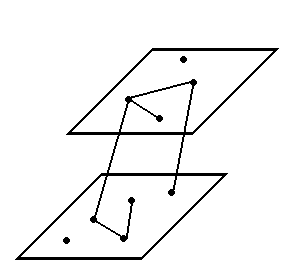
Замечание: Этот прием имеет практическое применение при проектировании сложных микросхем. Дело в том, что каждая микросхема – плоский граф, так как разные компоненты не должны пересекаться.

Если же граф не планарен, приходиться размещать микросхему в нескольких плоскостях.

Опр. Толщиной графа t(Г) – наименьшее количество параллельных плоскостей. В которых можно разместить вершины графа так, чтобы его ребра не пересекались.

Ясно, что t(Г)=1 для планарных графов.

t(Г)=≥2 для не планарных графов.

К сожалению, точного равенства для толщины графа не существует, но имеется одно неравенство:

t(Г)≥ 1 + int , где n –число вершин графов, Si – степени его вершин, длина, int –целая часть действительного числа.

Замечание: в языках программирования употребляется не менее 3 операций, превращающих действительное число в целое.

1)int() – получает целое число слева от данного

int(-2,8) = -3

int(2,8) = 2

2)trunk()

trunk(2,8)=2

trunk(-2,8)=-2

3) round() – округление числа до ближайшего целого

round(2,8)=3

round(-2,8)=-3

Найдем толщину графа №1

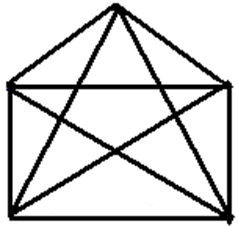N=5, si=4, ∑=4+4+4+4+4=20

t(Г)≥ 1 + int(( )=2

t(Г)≥2

Мы доказали другим способом, что граф непланарен.