Угловое перемещение, угловая скорость, угловое ускорение, их связь
с линейными величинами.
Угловое перемещение — векторная величина, характеризующая изменение угловой координаты в процессе её движения.
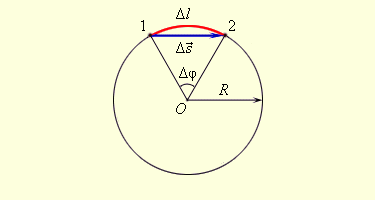
Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:
,
а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.
Единица измерения угловой скорости, принятая в системах СИ и СГС) — радианы в секунду. (Примечание: радиан, как и любые единицы измерения угла, — физически безразмерен, поэтому физическая размерность угловой скорости — просто [1/секунда]). В технике также используются обороты в секунду, намного реже — градусы в секунду, грады в секунду. Пожалуй, чаще всего в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли, просто «вручную» подсчитывая число оборотов за единицу времени.
Вектор
(мгновенной) скорости любой точки
(абсолютно) твердого тела, вращающегося
с угловой скоростью
определяется формулой:
где
— радиус-вектор к данной точке из начала
координат, расположенного на оси вращения
тела, а квадратными скобками обозначено
векторное произведение. Линейную
скорость (совпадающую с модулем вектора
скорости) точки на определенном расстоянии
(радиусе) r от оси вращения можно считать
так: v = rω. Если вместо радианов применять
другие единицы углов, то в двух последних
формулах появится множитель, не равный
единице.
В случае плоского вращения, то есть когда все векторы скоростей точек тела лежат (всегда) в одной плоскости («плоскости вращения»), угловая скорость тела всегда перпендикулярна этой плоскости, и по сути — если плоскость вращения заведомо известна — может быть заменена скаляром — проекцией на ось, ортогональную плоскости вращения. В этом случае кинематика вращения сильно упрощается, однако в общем случае угловая скорость может менять со временем направление в трехмерном пространстве, и такая упрощенная картина не работает.
Производная угловой скорости по времени есть угловое ускорение.
Движение с постоянным вектором угловой скорости называется равномерным вращательным движением (в этом случае угловое ускорение равно нулю).
Угловая скорость (рассматриваемая как свободный вектор) одинакова во всех инерциальных системах отсчета, однако в разных инерциальных системах отсчета может различаться ось или центр вращения одного и того же конкретного тела в один и тот же момент времени (то есть будет различной «точка приложения» угловой скорости).
В случае движения одной единственной точки в трехмерном пространстве можно написать выражение для угловой скорости этой точки относительно выбранного начала координат:
,
где
— радиус-вектор точки (из начала
координат),
— скорость этой точки.
—
векторное произведение,
— скалярное произведение векторов.
Однако эта формула не определяет угловую
скорость однозначно (в случае единственной
точки можно подобрать и другие векторы
,
подходящие по определению, по другому
— произвольно — выбрав направление
оси вращения), а для общего случая (когда
тело включает более одной материальной
точки) — эта формула не верна для угловой
скорости всего тела (так как дает разные
для каждой точки, а при вращении абсолютно
твёрдого тела по определению угловая
скорость его вращения — единственный
вектор). При всём при этом, в двумерном
случае (случае плоского вращения) эта
формула вполне достаточна, однозначна
и корректна, так как в этом частном
случае направление оси вращения заведомо
однозначно определено.
В случае равномерного вращательного движения (то есть движения с постоянным вектором угловой скорости) декартовы координаты точек вращающегося так тела совершают гармонические колебания с угловой (циклической) частотой, равной модулю вектора угловой скорости.
При измерении угловой скорости в оборотах в секунду (об/с), модуль угловой скорости равномерного вращательного движения совпадает с частотой вращения f, измеренной в герцах (Гц)
(то
есть в таких единицах
).
В
случае использования обычной физической
единицы угловой скорости — радианов в
секунду
—
модуль угловой скорости связан с частотой
вращения так:
Наконец,
при использовании градусов в секунду
связь с частотой вращения будет:
Углово́е ускоре́ние — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела.
При вращении тела вокруг неподвижной оси, угловое ускорение по модулю равно:
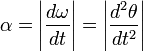
Вектор углового ускорения α направлен вдоль оси вращения (в сторону при ускоренном вращении и противоположно — при замедленном).
При вращении вокруг неподвижной точки вектор углового ускорения определяется как первая производная от вектора угловой скорости ω по времени, то есть
,
и направлен по касательной к годографу вектора в соответствующей его точке.
Существует связь между тангенциальным и угловым ускорениями:
где R — радиус кривизны траектории точки в данный момент времени. Итак, угловое ускорении равно второй производной от угла поворота по времени или первой производной от угловой скорости по времени. Угловое ускорение измеряется в рад/сек2 .