
- •3. Плоскости
- •3.1 Положение плоскости относительно плоскостей проекций
- •3.2 Плоскость общего положения
- •3.3 Плоскость уровня
- •3.4 Проецирующая плоскость
- •Вопросы для самопроверки
- •Тест № 3
- •4. Взаимное положение прямой и плоскости
- •4.1 Принадлежность прямой линии плоскости
- •4.2 Построение прямой в плоскости
- •4.3 Параллельность прямой и плоскости
- •4.4 Построение прямой линии, параллельной плоскости
- •4.5 Перпендикулярность прямой и плоскости
- •4.6 Теорема о проецировании прямого угла
- •4.7 Условие перпендикулярности прямой и плоскости
- •4.8 Построение перпендикуляра к плоскости
- •4.9 Пересечение прямой линии с плоскостью
- •4.10 Построение точки пересечения прямой с плоскостью
- •Вопросы для самопроверки
- •Тест № 4
- •Взаимное положение плоскостей
- •5.1 Параллельные плоскости
- •5.2 Построение параллельных плоскостей
- •5.3. Пересечение плоскостей
- •5.4 Построение линии пересечения двух плоскостей (1 способ)
- •5.5 Построение линии пересечения двух плоскостей (2 способ)
- •5.6 Перпендикулярные плоскости
- •1. В заданной плоскости проведите горизонталь h и фронталь f .
- •2. Из точки m опустите перпендикуляр к плоскости. A2f2 a1 h1 a
- •Тест № 5
- •6. Многогранники
- •6.1 Ортогональные проекции пирамиды
- •6.2 Точка на поверхности пирамиды
- •6.3 Призма
- •6.4 Ортогональные проекции призмы
- •6.5 Точка на поверхности призмы
- •Вопросы для самопроверки
- •Тест №5
- •7. Поверхность вращения
- •7.1 Конус
- •7.2 Ортогональные проекции конуса
- •7.3 Точки на поверхности конуса
- •7.4 Цилиндр
- •7.5 Точка на поверхности цилиндра
- •7.6 Сфера
- •7.7 Проекции сферы
- •7.8 Точка на поверхности сферы
- •7.9 Построение проекций точки На поверхности сферы
- •1 Случай
- •2 Случай
- •7.10 Поверхность тора
- •Точка на поверхности тора
- •Вопросы для самопроверки
- •Тест №6
- •8. Преобразование комплексного чертежа
- •Преобразование комплексного чертежа
- •8.1 Метод замены плоскостей проекций
- •8.2 Четыре основные задачи преобразования чертежа
- •8.3 Метрические задачи
- •8.3.1 Определение расстояний
- •Определить расстояние от точки м до прямой [ав]
- •Определить расстояние от точки м до плоскости (авс)
- •1. Преобразуйте плоскость общего положения в проецирующую плоскость применив третью основную задачу.
- •8.3.2 Определение углов
- •Определить угол между скрещивающимися прямыми
- •1.На комплексном чертеже постройте произвольную точку а.
- •Определить двугранный угол
- •1.Преобразуйте ребро [ав] общего положения в прямую уровня, применив первую основную задачу преобразования комплексного чертежа.
- •Вопросы для самопроверки
- •Тест №7
- •9. Пересечение поверхностей плоскостями
- •9.1 Пересечение пирамиды проецирующей плоскостью
- •9.2 Пересечение пирамиды плоскостью общего положения
- •9.3 Пересечение сферы плоскостью
- •9.4 Пересечение сферы плоскостью уровня
- •Пересечение сферы проецирующей
- •9.6 Построение линии пересечения сферы плоскостью уровня
- •9.7 Построение линии пересечения сферы фронтально проецирующей плоскостью
- •9.8 Пересечение конической поверхности плоскостью
- •Сечение - гипербола
- •3. Постройте промежуточные точки.
- •4. Соедините точки плавной линией (с учетом видимости).
- •Вопросы для самопроверки
- •Тест №8
- •10. Пересечение прямой c поверхностью.
- •Алгоритм решения первой главной позиционной задачи
- •10.1 Пересечение прямой с гранной поверхностью
- •1. Заключите прямую «а» во фронтально-проецирующую плоскость г. А г г п2
- •4. Линия m - треугольник (1-2-3). Горизонтальную проекцию линии m1 найдите ортогональным проецированием.
- •10.2 Пересечение прямой с поверхностью вращения
- •10.3 Пересечение прямой с конусом
- •10.4 Пересечение прямой с цилиндром
- •10.5 Пересечение прямой с поверхностью сферы
- •Вопросы для самопроверки
- •Тест №9
- •11. Пересечение кривых поверхностей
- •Алгоритм построения линии пересечения поверхностей.
- •11. 2 Способ вспомогательных концентрических сфер
- •11.3 Построение проекций линии пересечения поверхностей двух цилиндров
- •Вопросы для самопроверки
- •Тест №11
5.6 Перпендикулярные плоскости
Две плоскости
взаимно перпендикулярны, если одна из
них проходит через перпендикуляр к
другой.
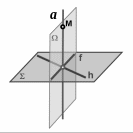
Рис.45
Прямая a
перпендикулярна
плоскости ,
следовательно,
плоскость ,
проходящая через прямую a,
будет перпендикулярна плоскости .
af,
ah
a
a


Дано:
(АВС)
M
Построить:
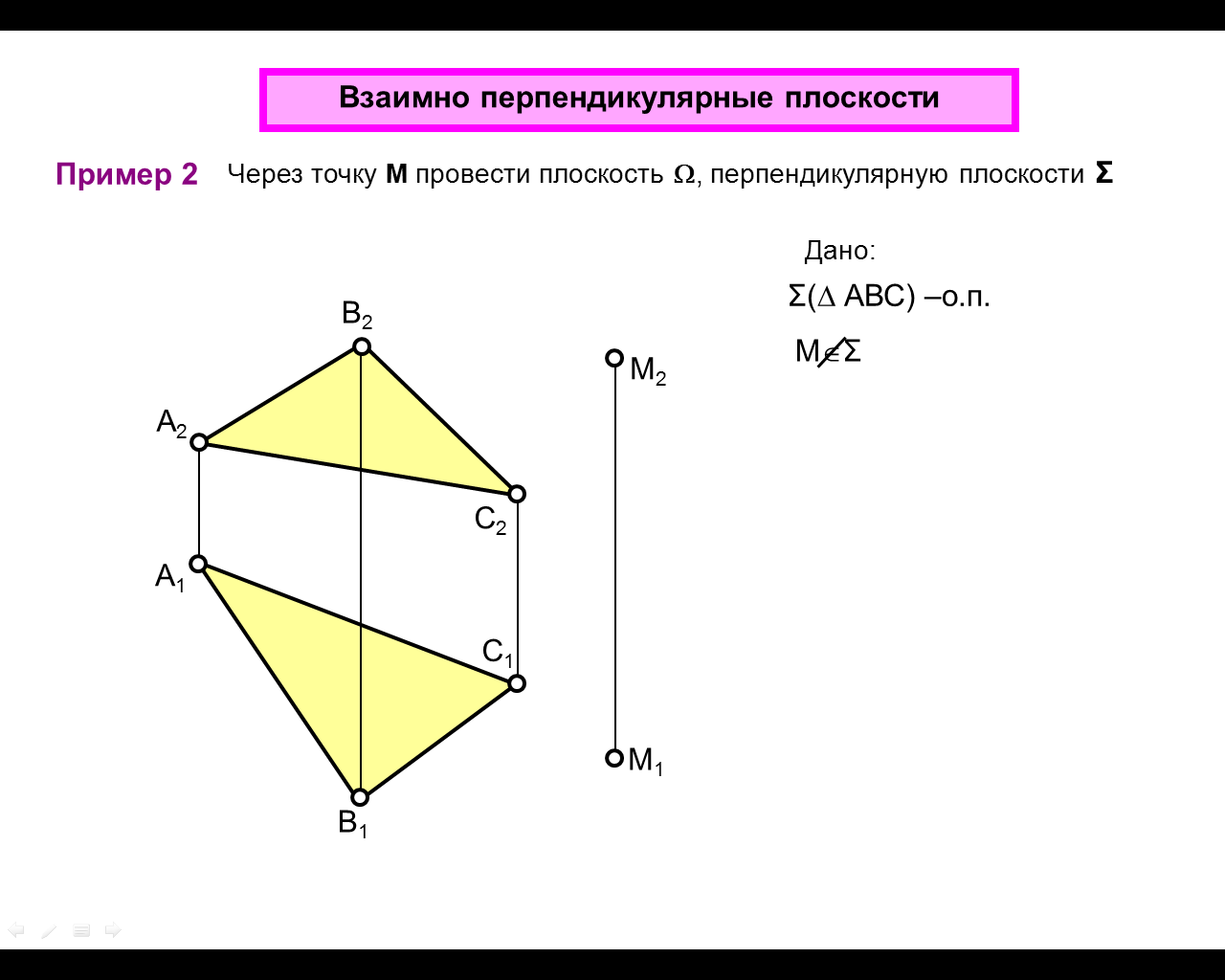
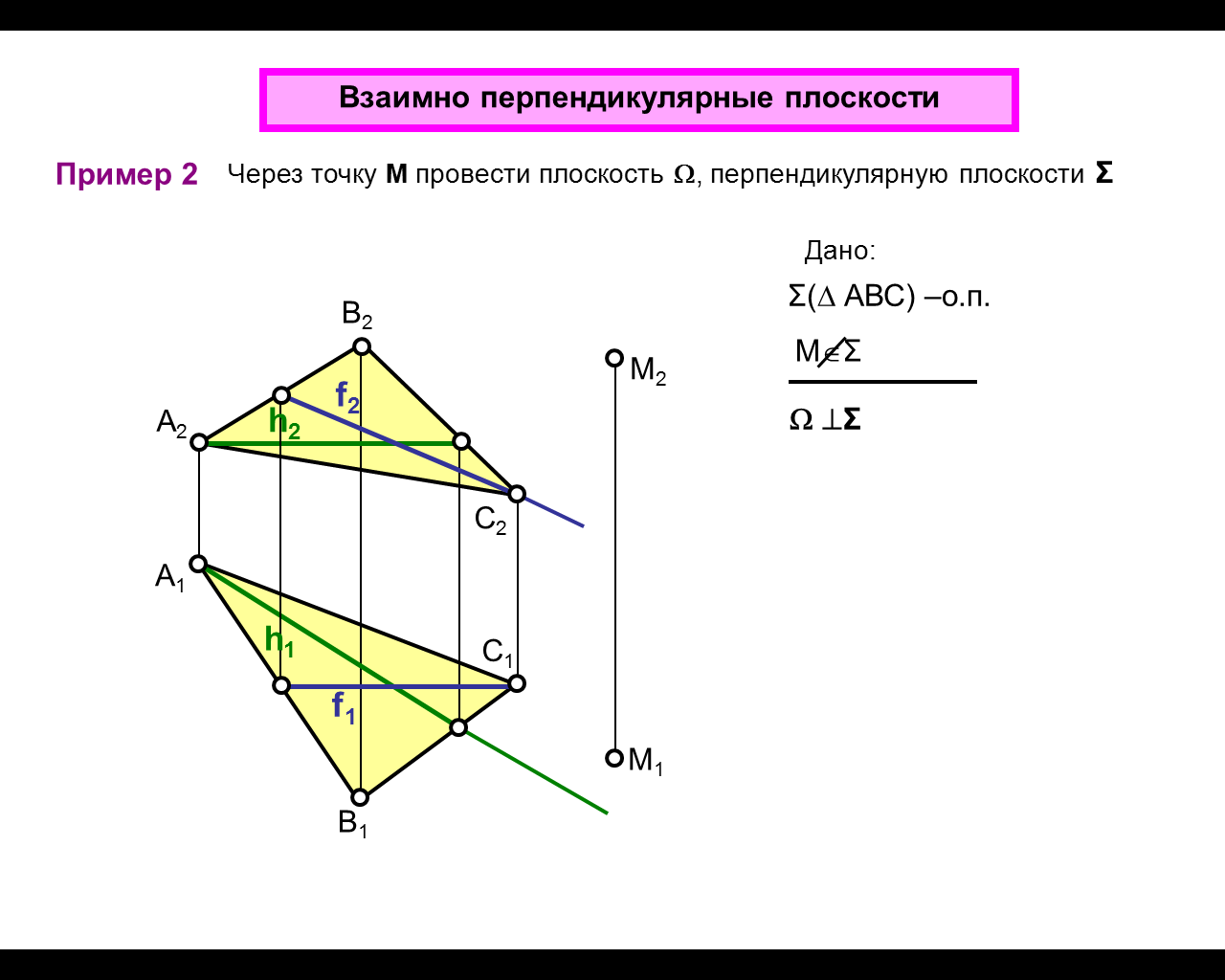

1. В заданной плоскости проведите горизонталь h и фронталь f .
2. Из точки m опустите перпендикуляр к плоскости. A2f2 a1 h1 a


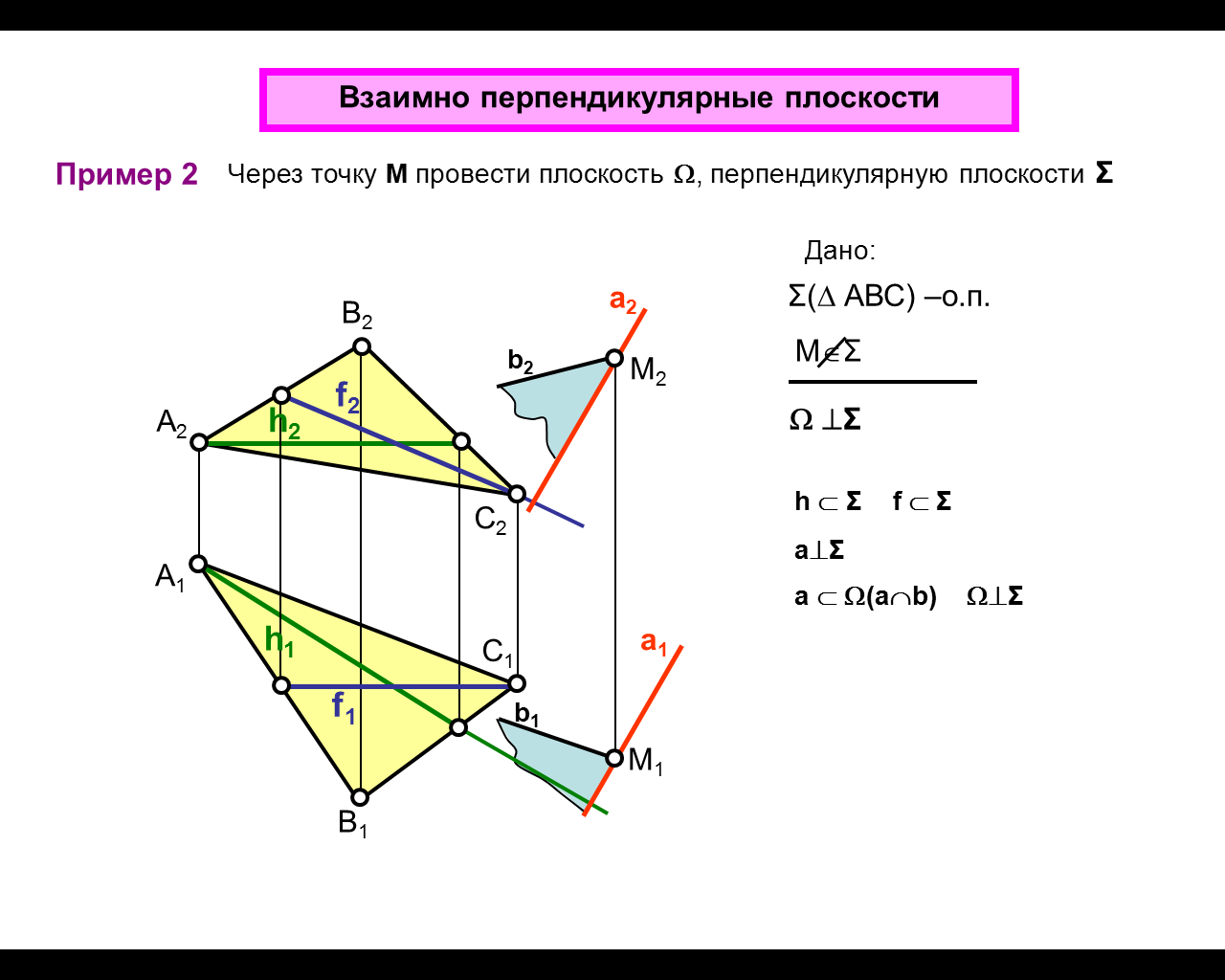
3. Из точки M
проведите прямую b
- общего
положения.
Пересекающиеся
прямые аb
задают плоскость .
Эта плоскость
(ab)
перпендикулярна заданной ,
т.к. она проходит через перпендикуляр
a.
a
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Когда плоскости параллельны?
2. Когда плоскости перпендикулярны друг другу?
3. Как строится линия пересечения двух плоскостей?
4. Как определяется видимость при пересечении двух плоскостей общего положения?
Тест № 5
1. Укажите чертеж параллельных плоскостей?
2. В каком случае Г и пересекаются и неперпендикулярны
между собой?
3.На каком чертеже заданы проекции двух взаимно
перпендикулярных плоскостей?
В каком случае Г и неперпендикулярны и непараллельны
между собой?
1
2
3
4
A2
2
B2
A2
C2
A1
B1
2



B2
C2
Г2
2
Г2







Г1
A1
B1
Г1
1
а1
1


C1
C1
1
6. Многогранники
Многогранники – это замкнутые поверхности, образованные некоторым количеством граней.
Пирамида – многогранник, у которого одна грань, принимаемая за основание, является многоугольником, а остальные грани – треугольники с общей вершиной.
Пирамиды бывают правильные и неправильные.
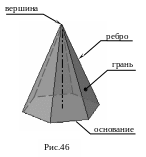 Правильной
пирамидой
называется такая пирамида, в основании
которой лежит правильный многоугольник
(рис 46), а боковые грани – равнобедренные,
равные между собой треугольники. Высота
пирамиды определяется длиной
перпендикуляра, опущенного из вершины
на плоскость основания.
Правильной
пирамидой
называется такая пирамида, в основании
которой лежит правильный многоугольник
(рис 46), а боковые грани – равнобедренные,
равные между собой треугольники. Высота
пирамиды определяется длиной
перпендикуляра, опущенного из вершины
на плоскость основания.
