3.4 Проецирующая плоскость

Проецирующая плоскость – плоскость, перпендикулярная одной плоскости проекций.

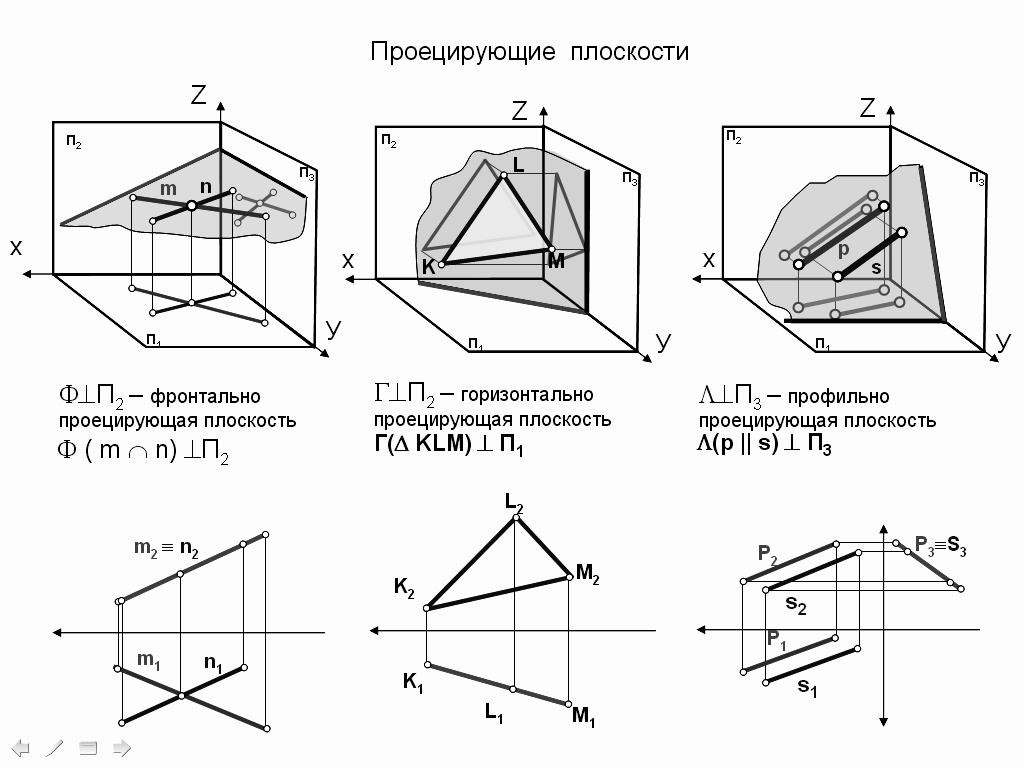Фронтально-проецирующая плоскость – плоскость (mn), перпендикулярная фронтальной плоскости проекций (рис. 32).

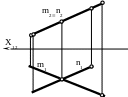
Рис.32

Фронтальная проекция плоскости представляет собой прямую линию, расположенную под некоторым углом к оси Х. На горизонтальную и профильную плоскости проекций любая фигура, распложенная в этой плоскости, проецируется с искажением.

Горизонтально-проецирующая плоскость – плоскость (KLM), перпендикулярная горизонтальной плоскости проекций (рис.33).

Горизонтальная проекция плоскости вырождается в прямую, расположенную под некоторым углом к оси Х.

На фронтальную и профильную плоскость проекций любая фигура, расположенная в плоскости, проецируется с искажением.

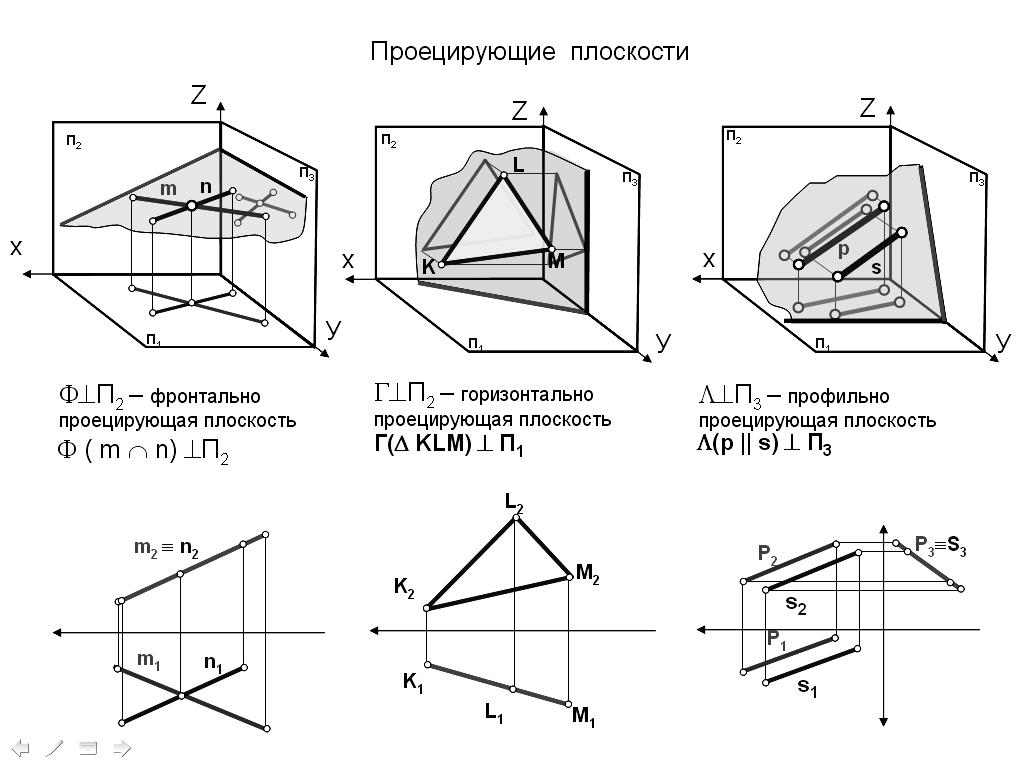
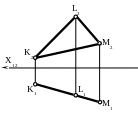
Рис.33

Профильно-проецирующая плоскость – плоскость (ps), перпендикулярная профильной плоскости проекций (рис. 34).

Профильная проекция плоскости вырождается в прямую, расположенную под некоторым углом к осям Y,Z.

На фронтальную и горизонтальную плоскость проекций любая фигура, расположенная в плоскости, проецируется с искажением.

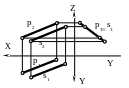
Рис.34

Вопросы для самопроверки

1. Какими способами можно задать плоскость на чертеже?

2. Какие плоскости называются плоскостями общего положения?

3. Какие плоскости называются проецирующими?

4. Какие плоскости называются плоскостями уровня?

Тест № 3

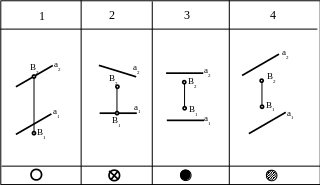
1. Укажите чертеж фронтально-проецирующей плоскости?

2. Укажите чертеж плоскости общего положения?

3. На каком чертеже показана фронтальная плоскость?

4 .Укажите чертеж профильно-проецирующей плоскости?

4. Взаимное положение прямой и плоскости

Прямая относительно плоскости может занимать следующие положения:

1. Прямая принадлежит плоскости.

2. Прямая параллельна плоскости.

3. Прямая пересекает плоскость.

4.1 Принадлежность прямой линии плоскости

При определении принадлежности прямой линии плоскости следует применить следующие аксиомы:

Аксиома 1. Прямая принадлежит плоскости, если две ее точки принадлежат этой плоскости.

Прямая принадлежит плоскости, если она имеет с плоскостью одну общую точку и параллельна какой-либо прямой расположенной в этой плоскости.

Аксиома 2. Точка принадлежит плоскости, если она принадлежит прямой этой плоскости.

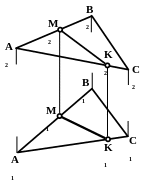
Рис.35

Прямая MK принадлежит плоскости (АВС) (рис.35), так как она проходит через точки М и K, расположенные на сторонах плоской фигуры.

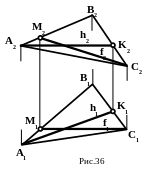
К прямым, занимающим особое положение в плоскости, относят горизонталь и фронталь (рис. 36).

Горизонталь – прямая h, лежащая в плоскости и параллельная горизонтальной плоскости проекций П₁.

Построение горизонтали начинают с фронтальной проекции, так как она параллельна оси X. h₂ X .

Фронталь – прямая f, лежащая в плоскости и параллельная фронтальной плоскости проекций П₂.

Построение фронтали начинают с горизонтальной проекции f₁  X.