
- •3. Плоскости
- •3.1 Положение плоскости относительно плоскостей проекций
- •3.2 Плоскость общего положения
- •3.3 Плоскость уровня
- •3.4 Проецирующая плоскость
- •Вопросы для самопроверки
- •Тест № 3
- •4. Взаимное положение прямой и плоскости
- •4.1 Принадлежность прямой линии плоскости
- •4.2 Построение прямой в плоскости
- •4.3 Параллельность прямой и плоскости
- •4.4 Построение прямой линии, параллельной плоскости
- •4.5 Перпендикулярность прямой и плоскости
- •4.6 Теорема о проецировании прямого угла
- •4.7 Условие перпендикулярности прямой и плоскости
- •4.8 Построение перпендикуляра к плоскости
- •4.9 Пересечение прямой линии с плоскостью
- •4.10 Построение точки пересечения прямой с плоскостью
- •Вопросы для самопроверки
- •Тест № 4
- •Взаимное положение плоскостей
- •5.1 Параллельные плоскости
- •5.2 Построение параллельных плоскостей
- •5.3. Пересечение плоскостей
- •5.4 Построение линии пересечения двух плоскостей (1 способ)
- •5.5 Построение линии пересечения двух плоскостей (2 способ)
- •5.6 Перпендикулярные плоскости
- •1. В заданной плоскости проведите горизонталь h и фронталь f .
- •2. Из точки m опустите перпендикуляр к плоскости. A2f2 a1 h1 a
- •Тест № 5
- •6. Многогранники
- •6.1 Ортогональные проекции пирамиды
- •6.2 Точка на поверхности пирамиды
- •6.3 Призма
- •6.4 Ортогональные проекции призмы
- •6.5 Точка на поверхности призмы
- •Вопросы для самопроверки
- •Тест №5
- •7. Поверхность вращения
- •7.1 Конус
- •7.2 Ортогональные проекции конуса
- •7.3 Точки на поверхности конуса
- •7.4 Цилиндр
- •7.5 Точка на поверхности цилиндра
- •7.6 Сфера
- •7.7 Проекции сферы
- •7.8 Точка на поверхности сферы
- •7.9 Построение проекций точки На поверхности сферы
- •1 Случай
- •2 Случай
- •7.10 Поверхность тора
- •Точка на поверхности тора
- •Вопросы для самопроверки
- •Тест №6
- •8. Преобразование комплексного чертежа
- •Преобразование комплексного чертежа
- •8.1 Метод замены плоскостей проекций
- •8.2 Четыре основные задачи преобразования чертежа
- •8.3 Метрические задачи
- •8.3.1 Определение расстояний
- •Определить расстояние от точки м до прямой [ав]
- •Определить расстояние от точки м до плоскости (авс)
- •1. Преобразуйте плоскость общего положения в проецирующую плоскость применив третью основную задачу.
- •8.3.2 Определение углов
- •Определить угол между скрещивающимися прямыми
- •1.На комплексном чертеже постройте произвольную точку а.
- •Определить двугранный угол
- •1.Преобразуйте ребро [ав] общего положения в прямую уровня, применив первую основную задачу преобразования комплексного чертежа.
- •Вопросы для самопроверки
- •Тест №7
- •9. Пересечение поверхностей плоскостями
- •9.1 Пересечение пирамиды проецирующей плоскостью
- •9.2 Пересечение пирамиды плоскостью общего положения
- •9.3 Пересечение сферы плоскостью
- •9.4 Пересечение сферы плоскостью уровня
- •Пересечение сферы проецирующей
- •9.6 Построение линии пересечения сферы плоскостью уровня
- •9.7 Построение линии пересечения сферы фронтально проецирующей плоскостью
- •9.8 Пересечение конической поверхности плоскостью
- •Сечение - гипербола
- •3. Постройте промежуточные точки.
- •4. Соедините точки плавной линией (с учетом видимости).
- •Вопросы для самопроверки
- •Тест №8
- •10. Пересечение прямой c поверхностью.
- •Алгоритм решения первой главной позиционной задачи
- •10.1 Пересечение прямой с гранной поверхностью
- •1. Заключите прямую «а» во фронтально-проецирующую плоскость г. А г г п2
- •4. Линия m - треугольник (1-2-3). Горизонтальную проекцию линии m1 найдите ортогональным проецированием.
- •10.2 Пересечение прямой с поверхностью вращения
- •10.3 Пересечение прямой с конусом
- •10.4 Пересечение прямой с цилиндром
- •10.5 Пересечение прямой с поверхностью сферы
- •Вопросы для самопроверки
- •Тест №9
- •11. Пересечение кривых поверхностей
- •Алгоритм построения линии пересечения поверхностей.
- •11. 2 Способ вспомогательных концентрических сфер
- •11.3 Построение проекций линии пересечения поверхностей двух цилиндров
- •Вопросы для самопроверки
- •Тест №11
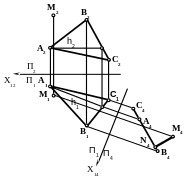
Определить расстояние от точки м до плоскости (авс)

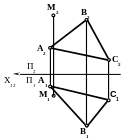
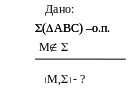
1. Преобразуйте плоскость общего положения в проецирующую плоскость применив третью основную задачу.
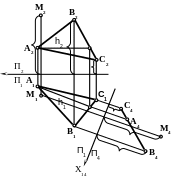
X12
П2
П4
П1
П4
(
h)
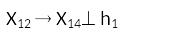

2.Кратчайшим
расстоянием от точки М до плоскости
является перпендикуляр, который на
плоскость проекций П4
спроецируется в натуральную величину.
[M4N4]
=M,

3. Прямая [MN]
в системе плоскостей проекций П1/П4
является
прямой уровня, значит
[M1N1]
Х14
4.Фронтальную
проекцию точки N2
построим по линии связи, предварительно
замерив расстояние от оси Х14
до N4
5. Постройте
фронтальную проекцию перпендикуляра.
Для этого соедините
отрезком прямой фронтальные проекции
N2
и M2
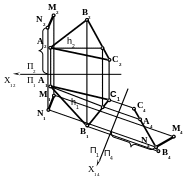
Расстояние между прямыми (параллельными или скрещивающимися) измеряется отрезком перпендикуляра между ними. Для решения необходимо одну из прямых (в случае параллельности – обе) преобразовать в положение проецирующей прямой, т.е. применить решение второй основной задачи преобразования комплексного чертежа.
8.3.2 Определение углов
К этой группе метрических задач относятся задачи на определение углов между двумя прямыми, прямой и плоскостью, двумя плоскостями.
Угол между пересекающимися прямыми. Если плоскость, определяемая этими прямыми, будет занимать положение плоскости уровня, то на паралллеьную плоскость проекций искомый угол будет проецироваться без искажения (рис.63), следовательно, для решения необходимо применить четвертую основную задачу преобразования комплексного чертежа.
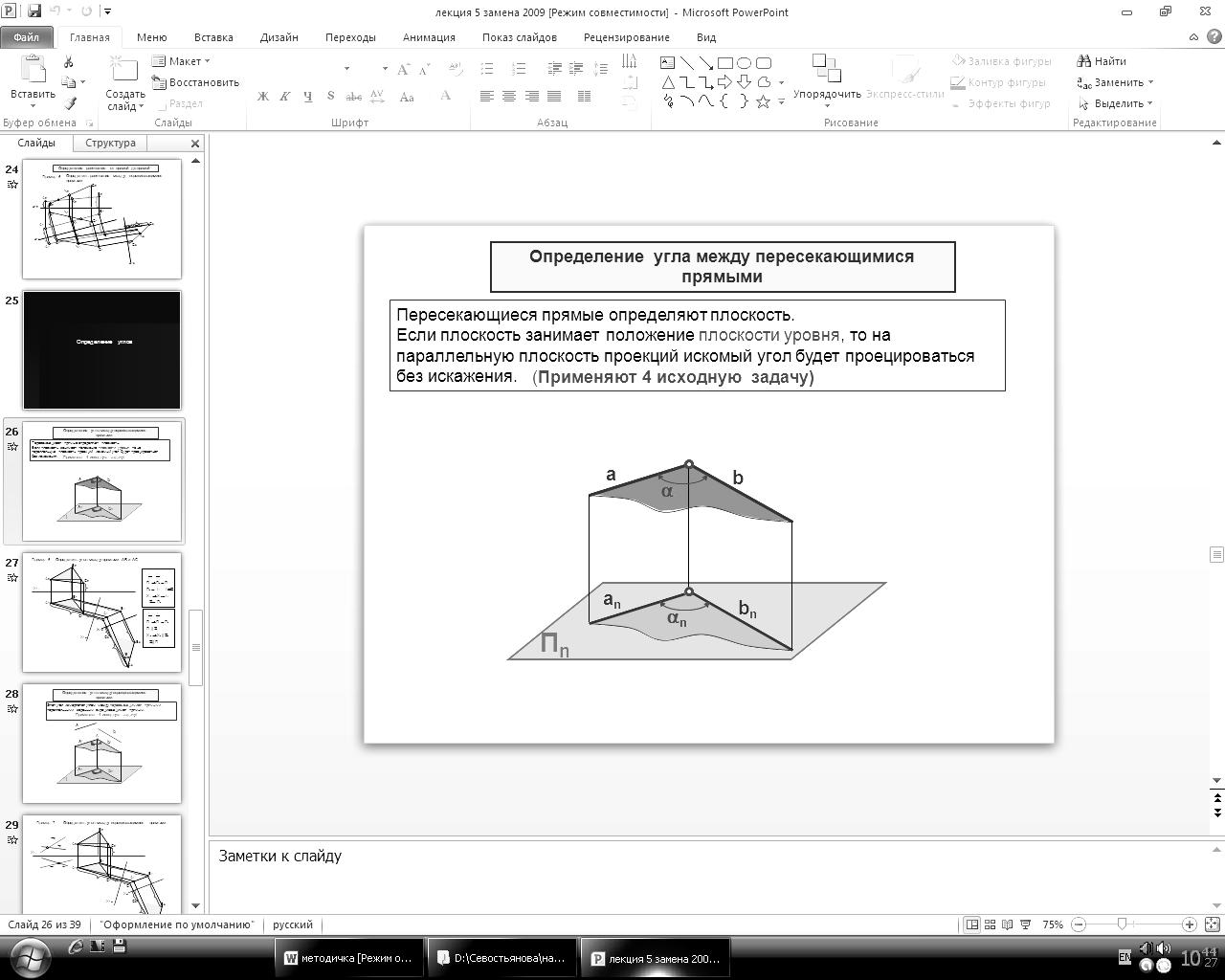
Рис. 63
Угол между скрещивающимися прямыми. Этот угол измеряется углом между пересекающимися прямыми, параллельными заданным скрещивающимся прямым (рис. 64), следовательно, после проведения вспомогательных прямых получаем предыдущую задачу.
a b
A
- произвольная точка.
aI
a;
bI
b
A
(
aI
bI)
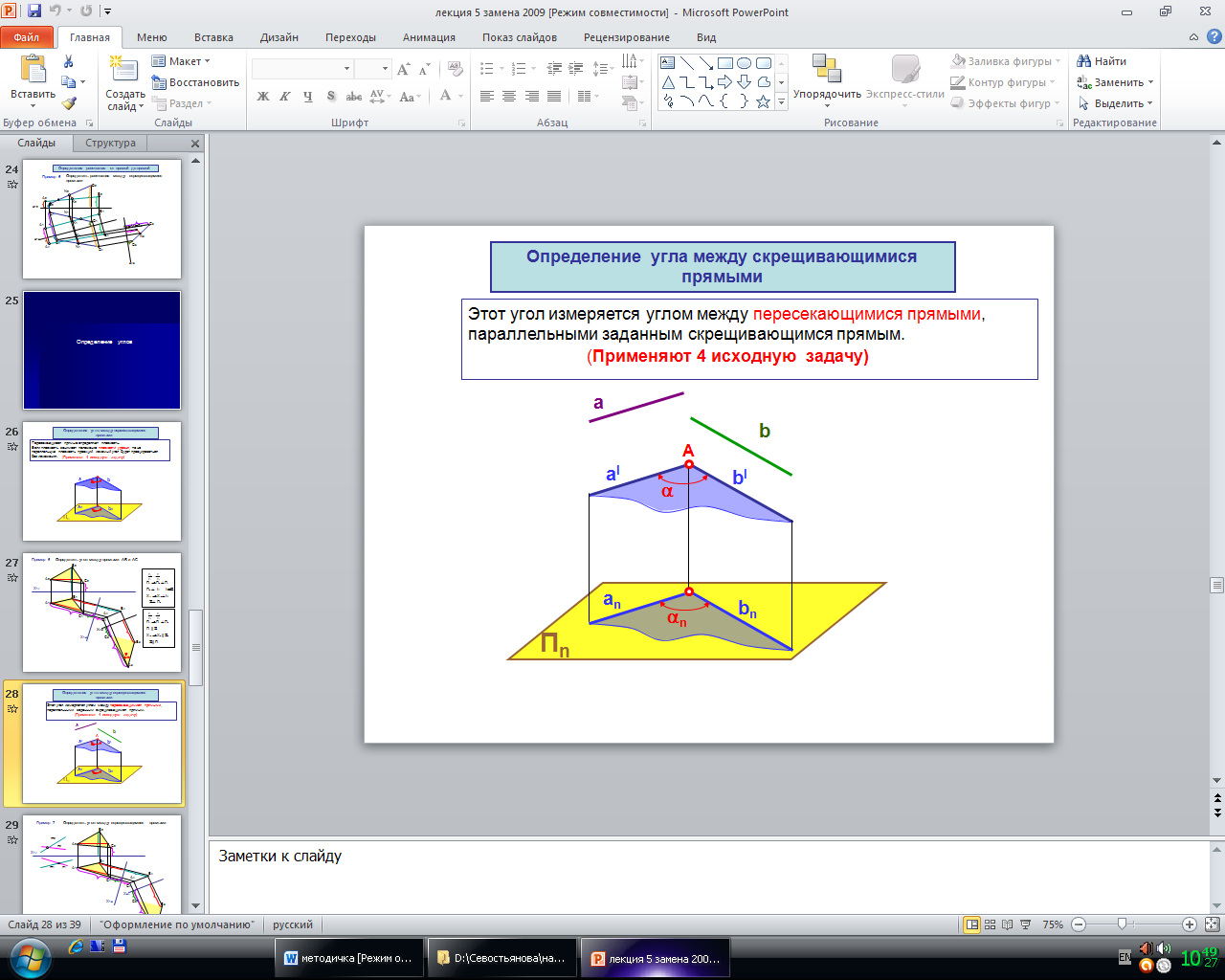

Рис. 64

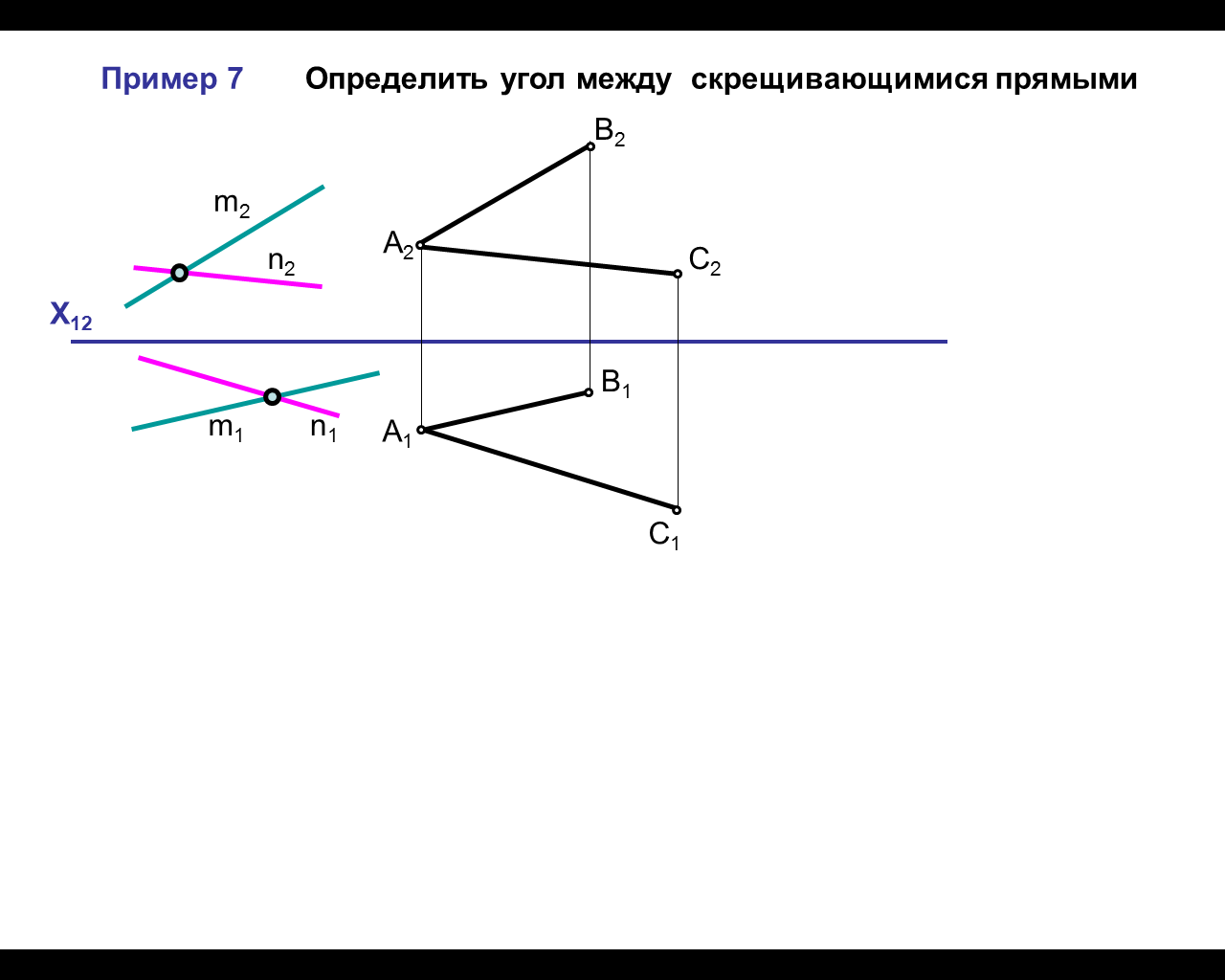
Определить угол между скрещивающимися прямыми

Дано:
m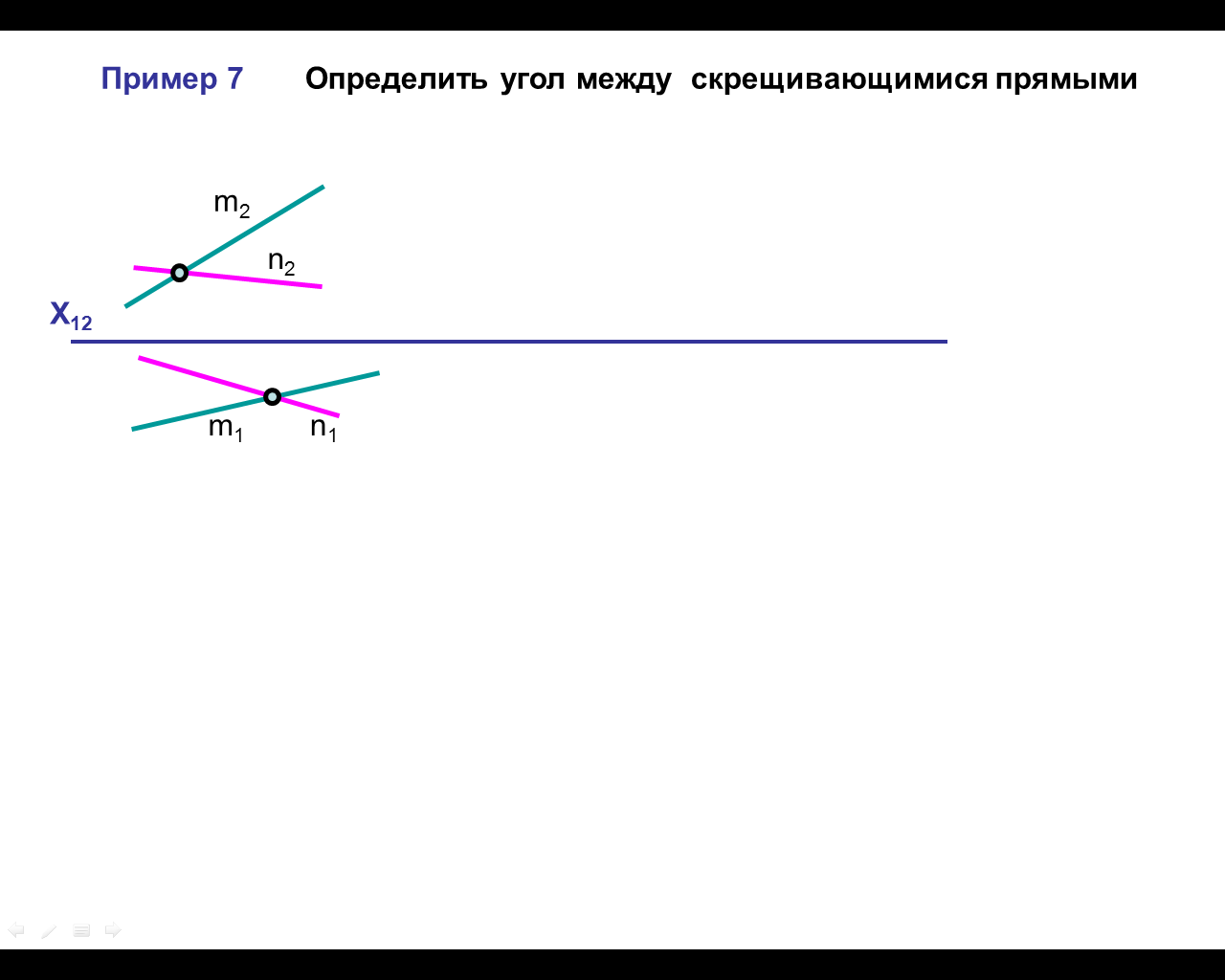
![]() n
n

1.На комплексном чертеже постройте произвольную точку а.

2.Через точку А
проведите две прямые, параллельные
двум заданным скрещивающимся прямым
[AB]m;
[AC]
n
[AB]
[AC]
=A
3. Две пересекающиеся
прямые задают плоскость
([AB]
[AC])
![]()
П2
П4
П1
П4
(h)
Х12
Х14
h1
X14
X45||
4
(А4В4С4)
П1
П5
П4
П4
||
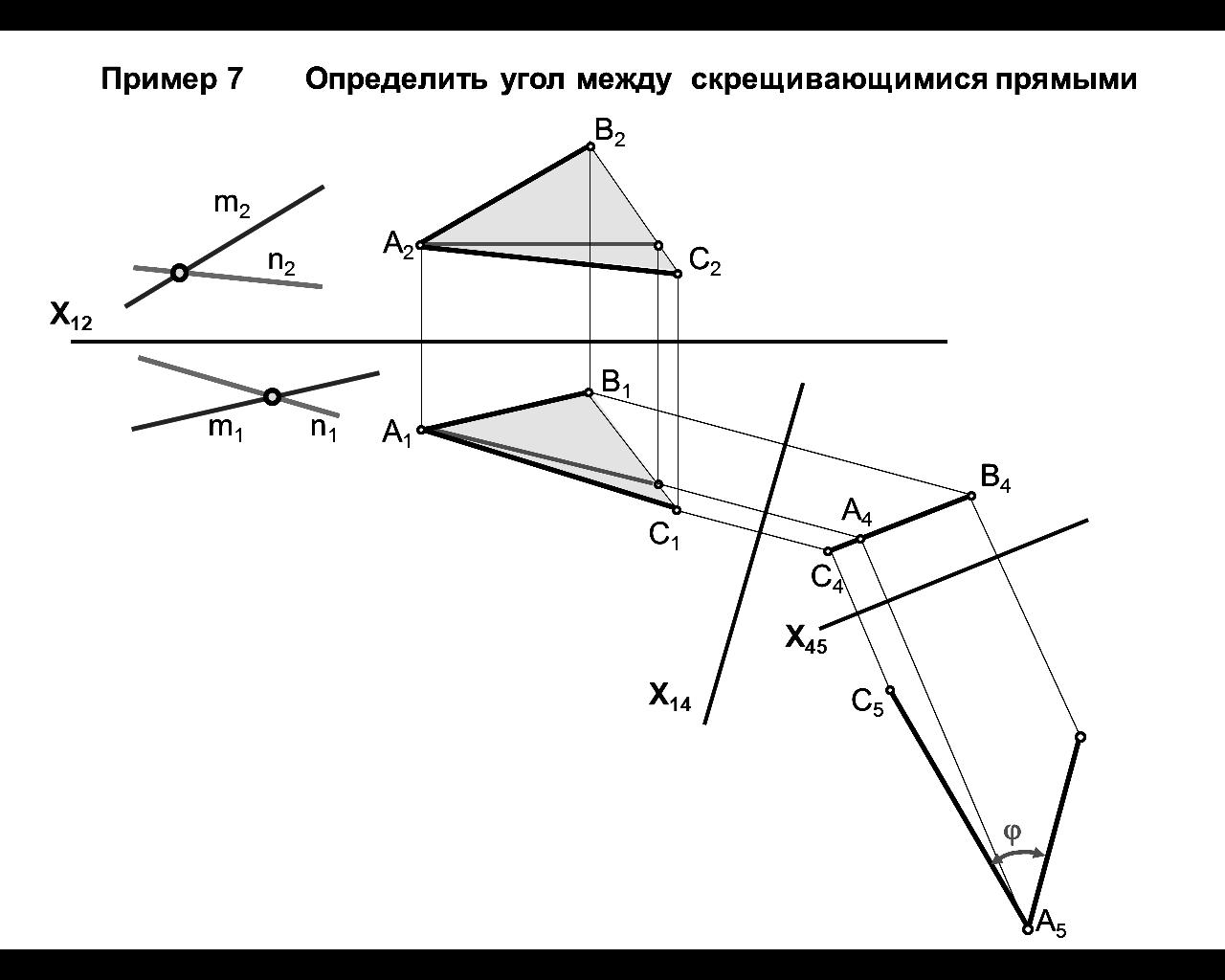
Применяя четвертую
основную задачу преобразования
комплексного чертежа, определите угол
между пересекающимися прямыми.
= m,
n


Угол между двумя плоскостями – двугранный угол. Плоскости и - грани этого угла, а линия пересечения этих плоскостей MN- ребро двугранного угла. Мерой измерения этого угла служит линейный (плоский) угол , полученный проецированием двугранного угла на плоскость проекций, перпендикулярной ребру MN (рис. 65).
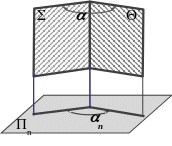
Рис. 65
