
- •3. Плоскости
- •3.1 Положение плоскости относительно плоскостей проекций
- •3.2 Плоскость общего положения
- •3.3 Плоскость уровня
- •3.4 Проецирующая плоскость
- •Вопросы для самопроверки
- •Тест № 3
- •4. Взаимное положение прямой и плоскости
- •4.1 Принадлежность прямой линии плоскости
- •4.2 Построение прямой в плоскости
- •4.3 Параллельность прямой и плоскости
- •4.4 Построение прямой линии, параллельной плоскости
- •4.5 Перпендикулярность прямой и плоскости
- •4.6 Теорема о проецировании прямого угла
- •4.7 Условие перпендикулярности прямой и плоскости
- •4.8 Построение перпендикуляра к плоскости
- •4.9 Пересечение прямой линии с плоскостью
- •4.10 Построение точки пересечения прямой с плоскостью
- •Вопросы для самопроверки
- •Тест № 4
- •Взаимное положение плоскостей
- •5.1 Параллельные плоскости
- •5.2 Построение параллельных плоскостей
- •5.3. Пересечение плоскостей
- •5.4 Построение линии пересечения двух плоскостей (1 способ)
- •5.5 Построение линии пересечения двух плоскостей (2 способ)
- •5.6 Перпендикулярные плоскости
- •1. В заданной плоскости проведите горизонталь h и фронталь f .
- •2. Из точки m опустите перпендикуляр к плоскости. A2f2 a1 h1 a
- •Тест № 5
- •6. Многогранники
- •6.1 Ортогональные проекции пирамиды
- •6.2 Точка на поверхности пирамиды
- •6.3 Призма
- •6.4 Ортогональные проекции призмы
- •6.5 Точка на поверхности призмы
- •Вопросы для самопроверки
- •Тест №5
- •7. Поверхность вращения
- •7.1 Конус
- •7.2 Ортогональные проекции конуса
- •7.3 Точки на поверхности конуса
- •7.4 Цилиндр
- •7.5 Точка на поверхности цилиндра
- •7.6 Сфера
- •7.7 Проекции сферы
- •7.8 Точка на поверхности сферы
- •7.9 Построение проекций точки На поверхности сферы
- •1 Случай
- •2 Случай
- •7.10 Поверхность тора
- •Точка на поверхности тора
- •Вопросы для самопроверки
- •Тест №6
- •8. Преобразование комплексного чертежа
- •Преобразование комплексного чертежа
- •8.1 Метод замены плоскостей проекций
- •8.2 Четыре основные задачи преобразования чертежа
- •8.3 Метрические задачи
- •8.3.1 Определение расстояний
- •Определить расстояние от точки м до прямой [ав]
- •Определить расстояние от точки м до плоскости (авс)
- •1. Преобразуйте плоскость общего положения в проецирующую плоскость применив третью основную задачу.
- •8.3.2 Определение углов
- •Определить угол между скрещивающимися прямыми
- •1.На комплексном чертеже постройте произвольную точку а.
- •Определить двугранный угол
- •1.Преобразуйте ребро [ав] общего положения в прямую уровня, применив первую основную задачу преобразования комплексного чертежа.
- •Вопросы для самопроверки
- •Тест №7
- •9. Пересечение поверхностей плоскостями
- •9.1 Пересечение пирамиды проецирующей плоскостью
- •9.2 Пересечение пирамиды плоскостью общего положения
- •9.3 Пересечение сферы плоскостью
- •9.4 Пересечение сферы плоскостью уровня
- •Пересечение сферы проецирующей
- •9.6 Построение линии пересечения сферы плоскостью уровня
- •9.7 Построение линии пересечения сферы фронтально проецирующей плоскостью
- •9.8 Пересечение конической поверхности плоскостью
- •Сечение - гипербола
- •3. Постройте промежуточные точки.
- •4. Соедините точки плавной линией (с учетом видимости).
- •Вопросы для самопроверки
- •Тест №8
- •10. Пересечение прямой c поверхностью.
- •Алгоритм решения первой главной позиционной задачи
- •10.1 Пересечение прямой с гранной поверхностью
- •1. Заключите прямую «а» во фронтально-проецирующую плоскость г. А г г п2
- •4. Линия m - треугольник (1-2-3). Горизонтальную проекцию линии m1 найдите ортогональным проецированием.
- •10.2 Пересечение прямой с поверхностью вращения
- •10.3 Пересечение прямой с конусом
- •10.4 Пересечение прямой с цилиндром
- •10.5 Пересечение прямой с поверхностью сферы
- •Вопросы для самопроверки
- •Тест №9
- •11. Пересечение кривых поверхностей
- •Алгоритм построения линии пересечения поверхностей.
- •11. 2 Способ вспомогательных концентрических сфер
- •11.3 Построение проекций линии пересечения поверхностей двух цилиндров
- •Вопросы для самопроверки
- •Тест №11
Точка на поверхности тора
Дано:
- открытый тор
А
Построить
недостающие проекции А.


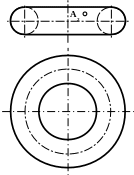
Точка «А» может
находиться как на наружной, так и на
внутренней поверхности тора. Рассмотрим
возможные варианты. Для нахождения
горизонтальных проекций точек
воспользуемся вспомогательной секущей
плоскостью Г (можно решать задачу с
помощью принадлежности точек линии
–параллели).
1.Через фронтальную
проекцию точки «А» проведите секущую
плоскость Г, перпендикулярно оси
вращения.
Из (рис.61)
видно, что в сечении получатся две
окружности.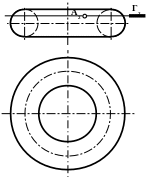
2.Замерьте радиус
малой окружности. Для этого определите
радиус R
(от оси
вращения до точки 12)
3. На горизонтальной
проекции тора, из центра О1
проведите окружность радиусом R
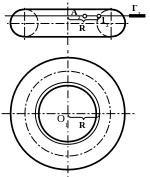

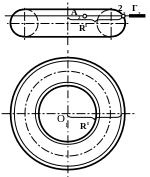
4. Замерьте радиус,
большой окружности RI
(от оси вращения до фронтальной проекции
точки 22).
5. На горизонтальной
проекции тора, из О1
проведите окружность радиусом RI.
6. Спроецируйте
точку «А» на горизонтальные проекции
малой и большой окружностей.
Получатся четыре
проекции : А1,
А1III
и А1I,
А1II
Таким образом,
возможны четыре случая:
А, АIII
– точки расположены
на наружной
поверхности тора;
А
I,
АII-
точки расположены на внутренней
поверхности тора.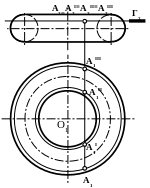
Вопросы для самопроверки
1. Какие поверхности называются поверхностями вращения?
2. Назовите главные линии поверхности вращения ?
3. Как определяется поле видимых точек относительно П2, П1, П3 ?
4. Как определяется порядок поверхности?
5. С помощью какой линии строятся недостающие проекции точек, принадлежащих поверхности вращения?
Тест №6
1. Какая из линий сферы является главным фронтальным
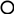 меридианом?
меридианом?
2. Какая из линий сферы является экватором?
3. Какая из линий сферы является главным профильным
меридианом?
4. Какая из линий сферы является параллелью?
8. Преобразование комплексного чертежа
Решение пространственных задач упрощается, если геометрические элементы занимают частное положение. Для этого преобразуют комплексный чертеж.
Существует два вида преобразования комплексного чертежа.
